
- \(2\)種類のヨウ素滴定
- 速攻で解く方法
を特にポイントとしています.昨日の自分より少しでもレベルアップしていきましょう!
ヨウ素滴定の種類
ヨウ素滴定の学習を進めるためには,ヨウ素の性質を理解しておく必要があります.以下の記事で少し解説していますので,そちらもみてみてください.

\(\rm{I_2\ +\ }\)\(2e^-\ →\ \rm{2I^-}\)
この反応であれば,\(\rm{I_2 → 2I^-}\)への変化で\(e^-\)を受け取っています.\(\rm{I_2}\)は酸化剤として作用しています.
一方で,上の反応は逆に\(\rm{2I^- → I_2}\)のような反応も起こります.
\(\rm{2I^-\ →\ I_2\ +\ }\)\(2e^-\)
このときは\(e^-\)を放出しているので,\(\rm{I^-}\)は還元剤として作用しています.
つまり,ヨウ素は酸化剤・還元剤のどちらとしてのパワーももっているので,ヨウ素滴定も\(2\)種類あるというわけです.ヨウ素が酸化剤として作用するものをヨウ素酸化滴定(ヨージメトリー\(\rm{:Iodimetry}\)),還元剤として作用するものをヨウ素還元滴定(ヨードメトリー\(\rm{:Iodometry}\))といいます.
- ヨウ素が酸化剤として作用→ヨウ素酸化滴定(ヨージメトリー)
- ヨウ素が還元剤として作用→ヨウ素還元滴定(ヨードメトリー)
ヨウ素酸化滴定では,還元性物質を\(\rm{I_2}\)によって直接滴定します.一方で,ヨウ素還元滴定では,酸化性物質に\(\rm{I^-}\)を作用させて\(\rm{I_2}\)を生成し,これをチオ硫酸ナトリウム水溶液で間接滴定します.直接滴定できるか,他の物質を介して滴定するかが,この\(2\)つの滴定の決定的な違いになります.
それでは順番に詳しく解説していきましょう.
ヨウ素酸化滴定(ヨージメトリー)
ヨウ素酸化滴定(ヨウ素が酸化剤として作用する)では,還元性のある物質をヨウ素溶液(\(\rm{I_2}\))によって「直接滴定」します.先ほどもこの点を強調しましたが,ヨウ素還元滴定でこの違いが大切になるので覚えておいてくださいね!
問題の流れを解説したあと,私独自の高速で解く方法を解説していきます.
ヨウ素酸化滴定の流れ
\(\rm{0.10\ mol/L}\)のヨウ素溶液\(\rm{50\ mL}\)に,ある一定量の二酸化硫黄を反応させた.この溶液に残ったヨウ素を定量するために,デンプンを指示薬として加えた.\(\rm{0.050\ mol/L}\)のチオ硫酸ナトリウム水溶液で滴定したところ,\(\rm{25\ mL}\)を加えたときに溶液の色が変化した.
反応させた二酸化硫黄の物質量は?
ステップ\(1:\)ヨウ素溶液の作製
ヨウ素を溶液に溶かして,ヨウ素溶液を作ります.このとき,ヨウ素は無極性分子なので,極性分子である水にほとんど溶けません.そこで,ヨウ素をヨウ化カリウム水溶液(\(\rm{KI}\))に溶かします.このとき,以下のような平衡関係によってヨウ素(\(\rm{I_2}\))を溶かすことができます.
\(\rm{I_2\ +\ I^-\ ⇄\ {I_3}^-}\)
この場合,\(\rm{KI}\)は\(\rm{I_2}\)を溶かす溶媒として働いています.
ステップ\(2:\)還元剤を投入
ステップ\(1\)で作製したヨウ素溶液に還元剤を投入して酸化還元反応をさせます.今回の問題では二酸化硫黄\(\rm{SO_2}\)が還元剤であるため,\(\rm{SO_2}\)を投入します.還元剤の\(\rm{SO_2}\)は\(\rm{{SO_4}^{2-}}\)へと変化します.
\(\rm{SO_2\ +\ 2H_2O\ →\ {SO_4}^{2-}\ +\ 4H^+\ +\ }\)\(2e^-\)
\(\rm{SO_2}\)は酸化剤としても還元剤としても作用します.合わせておさえておいてくださいね!
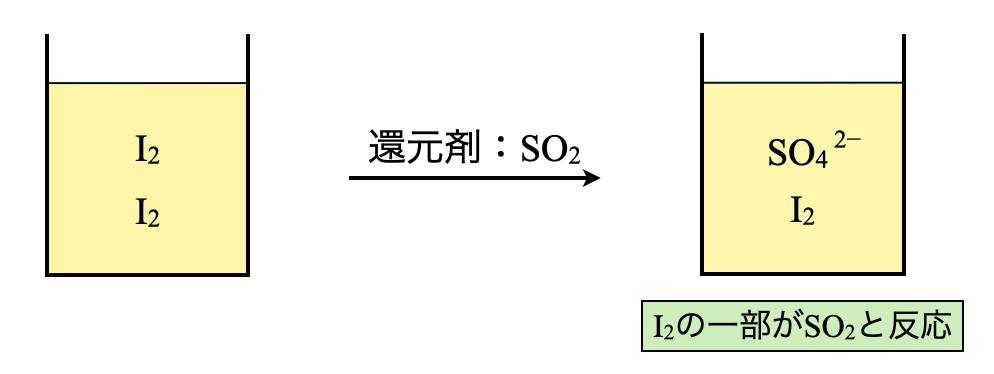
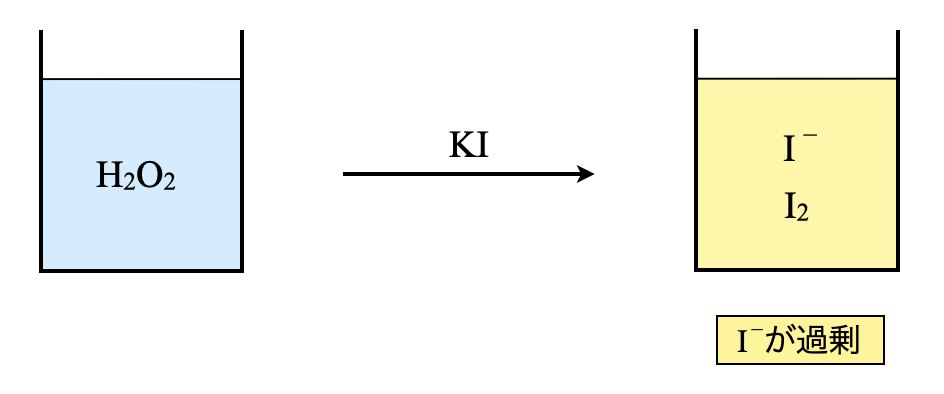
線分図で考えると下のような定量関係になります.ヨウ素溶液中の\(\rm{I_2}\)の一部が\(\rm{I^-}\)となり,\(\rm{I_2}\)が過剰なため,\(\rm{I_2}\)が一部残存している状態になっています.

ヨウ素は中程度の酸化剤なので,滴定には比較的強い還元剤である\(\rm{H_2S}\),\(\rm{SO_2}\),\(\rm{Sn^{2+}}\)などでしか定量できません.その中から今回は\(\rm{SO_2}\)を使っています!
ステップ\(3:\)デンプンの仕込み
ステップ\(2\)で残存していた\(\rm{I_2}\)に\(\rm{Na_2S_2O_3}\)を加えることで,滴定していきます.ただ,\(\rm{I_2}\)(褐色)を還元していくと,次第に淡くなり,ちょうど無色になった点が当量点となります.実際に実験をするとわかるのですが,次第に淡くなって,無色の点を正確に確認するのは困難です.
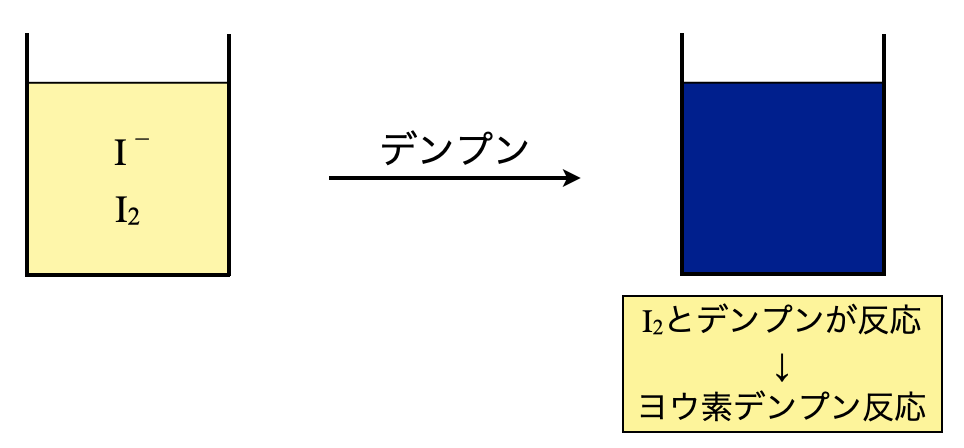
そこでわかりやすくするために,少量のデンプン水溶液を仕込みます.すると,溶液は鮮やかな青紫色を呈します.これが中学校から習ってきたヨウ素デンプン反応です.この呈色反応は鋭いので,無色になった点を見極めることができ,滴定の終点も把握しやすくなります.
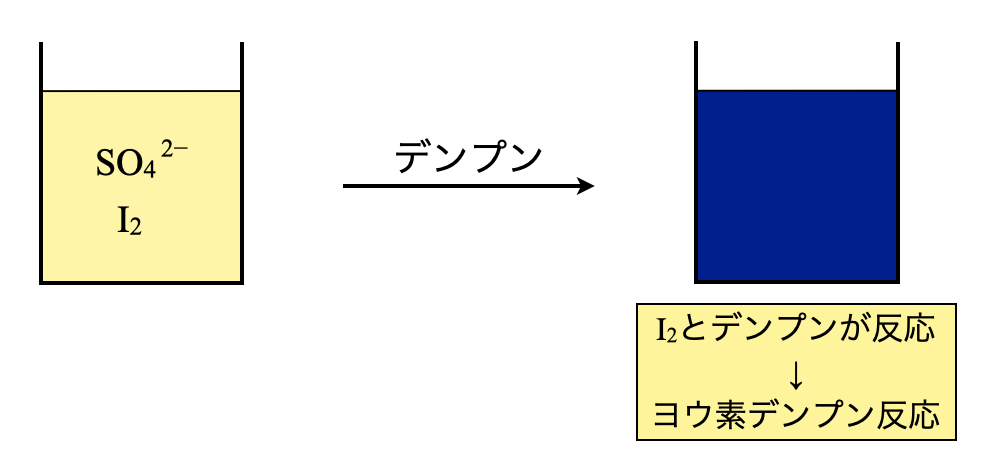
ステップ\(4:\)チオ硫酸ナトリウム(\(\rm{Na_2S_2O_3}\))で滴定
ステップ\(3\)でデンプンを加えたことで,滴定の終点がわかりやすくなりました.残存している\(\rm{I_2}\)を\(\rm{Na_2S_2O_3}\)で滴定していきます.
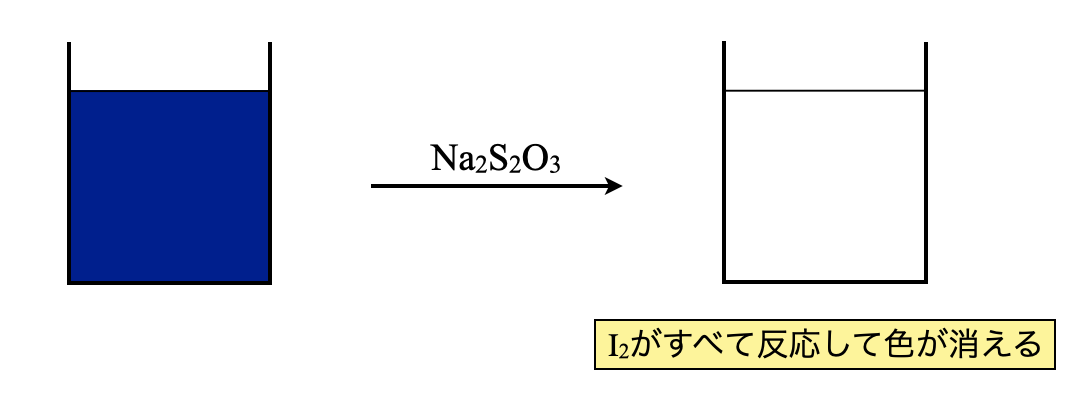

ヨウ素酸化滴定の解き方
それではヨウ素酸化滴定(ヨージメトリー)の流れを理解したところで,私独自の高速で解く方法を解説していきます.たったの\(2\)つのポイントで速攻で解くことができます.
ポイント\(2:e^-\)の物質量の差を見抜く
ポイント\(1:\)線分図を書いて,今回の物質量関係を図示する
今回の問題を線分図に書いていきましょう.

ポイント\(2:e^-\)の物質量の差を見抜く
先ほどの線分図を見ると,\(\rm{I_2}\)由来の\(e^-\)と\(\rm{SO_2}\)由来の\(e^-\)の差に注目することが大切です.この差が\(\rm{Na_2S_2O_3}\)由来の\(e^-\)と等しくなる点が滴定の当量点となります.
これをふまえて\(e\)リングで考えると,\(\rm{{S_2O_3}^{2-}}\)由来の\(e^-\)と\(\rm{SO_2}\)由来の\(e^-\)の合計が\(\rm{I_2}\)由来の\(e^-\)と等しくなります.ここで\(\rm{I_2}\)の物質量は\(\rm{5.0\ mmol}\)なので,\(\rm{I_2}\)由来の\(e^-\)は\(\rm{5.0 × 2 = 10\ mmol}\)となります.これをふまえて実際に計算していきましょう.
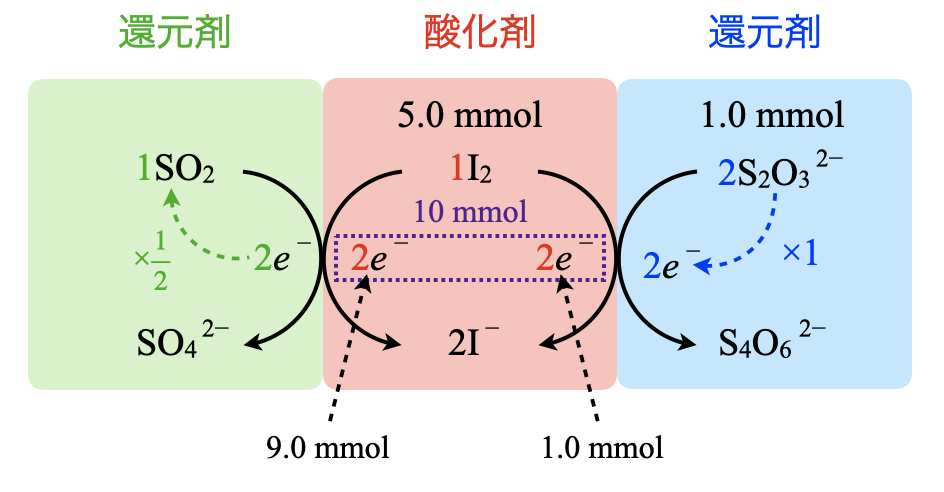
・\(\rm{I_2}\)
全\(\rm{I_2:0.10 × 50 = 5.00\ mmol}\)
\(e^-:5.00 × 2 = 10.0\ \rm{mmol}\)
・\(\rm{{S_2O_3}^{2-}}\)
加えた\(\rm{{S_2O_3}^{2-}:0.050 × 20 = 1.0\ mmol}\)
\(e^-:1.0\ \rm{mmol}\)
そしてこの差\(\rm{:10.0\ -\ 1.0 = 9.0\ \rm{mmol}}\)が\(\rm{SO_2}\)由来の\(e^-\)であるとわかります.このまま,\(\rm{SO_2 → {SO_4}^{2-}}\)についても同じように考えると,\(\rm{SO_2}\)の物質量を求めることができます.いつもとは求める順序が違うので注意してくださいね!
・\(\rm{SO_2}\)
\(e^-:9.0\ \rm{mmol}\)
\(\rm{SO_2:9.0 × \large \frac{1}{2} \small = 4.5\ mmol = 4.5 × 10^{-3}\ mol}\)
と求めることができます.
酸化還元では,この\(e\)リングを使いこなせるようになるのが速く解くコツなので,ぜひ自分のものにしてくださいね!このサイトではこれからもこの解き方をしていくので.わからない問題があればぜひ参考にしてくださいね!
ヨウ素還元滴定(ヨードメトリー)
それでは次に,ヨウ素還元滴定(ヨードメトリー)について解説していきます.
ヨウ素還元滴定(ヨウ素が還元剤として作用する)では,酸化性のある物質をにヨウ素イオン(\(\rm{I^-}\))を作用させて\(\rm{I_2}\)とし,これをチオ硫酸ナトリウムで「間接的に滴定」します.今回も問題の流れを解説したあと,同じように速攻で解く方法を解説していきます.
ヨウ素酸化滴定との違いを意識しながら解説していきます!
ヨウ素還元滴定の流れ
濃度未知の過酸化水素水\(\rm{10\ mL}\)に,過剰のヨウ化カリウムの硫酸酸性水溶液を加えたところ,ヨウ素が遊離した.この溶液にデンプンを指示薬として加え,\(\rm{0.10\ mol/L}\)のチオ硫酸ナトリウム水溶液で滴定したところ,\(\rm{10\ mL}\)加えたところで溶液の色が変化した.
もとの過酸化水素水のモル濃度は?
今回の問題ではヨウ素を還元剤とするので,酸化剤である\(\rm{H_2O_2}\)を滴定していきます.
少しややこしいですが,丁寧に解説するのでついてきてくださいね!
ステップ\(\rm{1:H_2O_2}\)に過剰のヨウ化カリウムを投入
濃度未知の\(\rm{H_2O_2}\)に過剰の\(\rm{KI}\)の硫酸酸性水溶液を加えていきます.ここで酸化還元反応が起こり,\(\rm{I^-}\)の一部が\(\rm{I_2}\)へと変化します.

この問題では酸性条件にするために硫酸を用いていますが,これについて解説しておきます.
溶液を酸性にするためには,塩酸や硝酸などの方法も考えられます.ここで塩酸を加えると,\(\rm{HCl}\)が還元剤として働き,\(\rm{Cl^-→Cl_2}\)に酸化されてしまいます.同様に硝酸を用いると,\(\rm{{NO_3}^-}\)が酸化剤として働き,還元剤の一部が酸化されてしまいます.どちらの場合にしても滴定したい物質の一部が消費されてしまったことになるので,滴定値に誤差が生じてしまいます.
一方で,硫酸は酸化力も還元力もないため,ただの酸として使うことができるというわけです.よって,酸化還元反応で酸性にするために硫酸を用いています.
問題の本質とは異なるところでつまずいてしまう人も多いため,疑問を残さないようにしておきましょう.
ステップ\(2:\)デンプンの仕込み
今回はステップ\(2\)でデンプンを仕込んでいきます.当量点を見極めるために,デンプンを仕込み,ヨウ素デンプン反応をさせます.これによって,溶液が青紫色を呈します.
ステップ\(3:\)酸化剤を投入
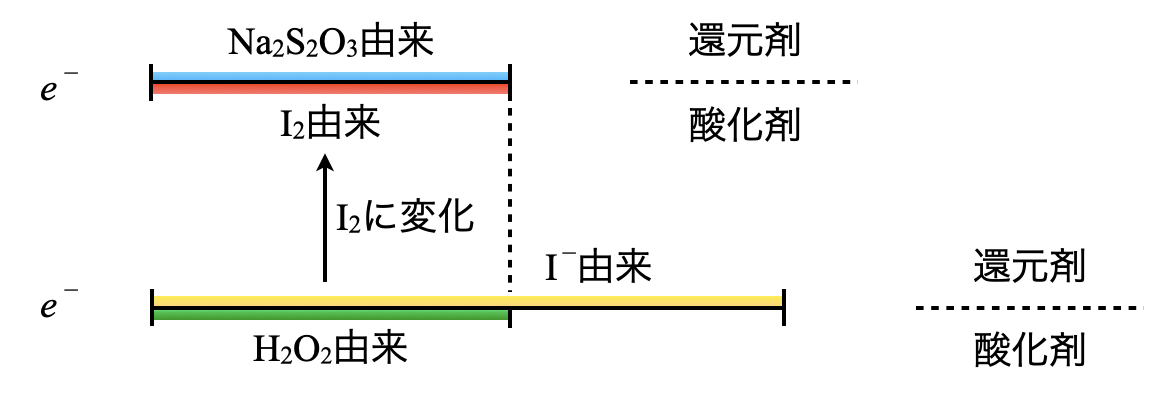
ステップ\(1\)で反応させた\(\rm{I_2}\)を酸化剤(今回の問題では\(\rm{Na_2S_2O_3}\))で滴定していきます.ヨウ素酸化滴定との違いは残存している物質を滴定するのではなく,ステップ\(1\)で酸化還元反応で生成した\(\rm{I_2}\)を滴定している点です.
\(e^-\)の流れを考えていくと,\(\rm{S_2O_3 → I_2 → H_2O_2}\)という流れで\(\rm{H_2O_2}\)の濃度を知ることができます.\(\rm{I_2}\)を間に介しているため,間接的に滴定していると先ほど説明したのです.
ヨウ素還元滴定の解き方
それではヨウ素還元滴定(ヨードメトリー)の流れを理解したところで,私独自の高速で解く方法を解説していきます.今回もたったの\(2\)つのポイントで速攻で解くことができます.
ポイント\(2:e^-\)の物質量の関係性を見抜く
ポイント\(1:\)線分図を書いて,今回の物質量関係を図示する今回の問題を線分図に書いていきましょう.

ポイント\(2:e^-\)の物質量の関係性を見抜く
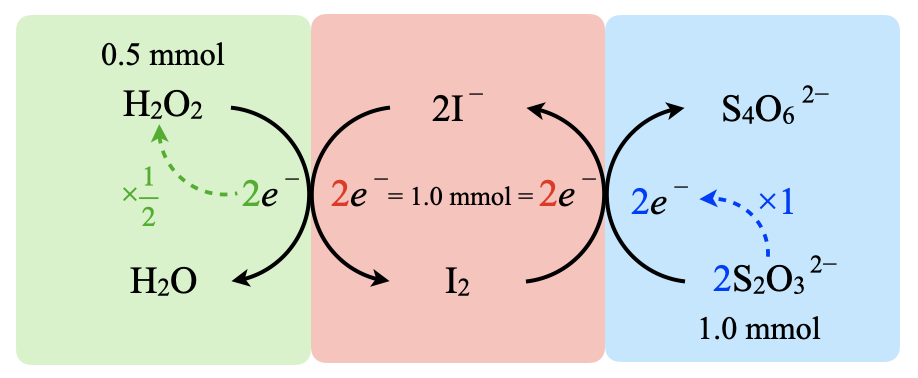
先ほどの線分図を見ると,\(\rm{H_2O_2}\)由来,\(\rm{{S_2O_3}^{2-}}\)由来の\(e^-\)が等しくなります.これをふまえて実際に計算していきましょう.
・\(\rm{{S_2O_3}^{2-}}\)
加えた\(\rm{{S_2O_3}^{2-}:0.10 × 10 = 1.0\ mmol}\)
\(e^-:1.0\ \rm{mmol}\)
・\(\rm{I^-}\)
\(e^-:1.0\ \rm{mmol}\)
\(\rm{I_2}\)に変化した\(\rm{I^-:1.0 × \large \frac{1}{2} \small = 0.5\ mmol}\)
・\(\rm{H_2O_2}\)
\(e^-:0.5\ \rm{mmol}\)
反応した\(\rm{H_2O_2:0.5\ mmol}\)
\(\rm{H_2O_2}\)の物質量がわかったので,その濃度を求めていきます.
\(\rm{H_2O_2}\)濃度\(\rm{:\large \frac{0.5\ mmol}{10\ mL} \small = 5.0 × 10^{-2}\ mol/L}\)
今回も一連の\(e\)リングを使って解説しました.ぜひ流れを理解した上で,解けるように練習しておきましょう!



コメント