【受験合格への珠玉の3題】この3題をマスターして受験を制覇しよう！！

\((2)\) \(\rm{1.0 × 10^{-5}\ mol/L}\)の塩酸を純水で\(1000\)倍に希釈した溶液の\(\rm{pH}\)は？
ただし、\(\rm{log_{10}1.05=0.02}\)とする。

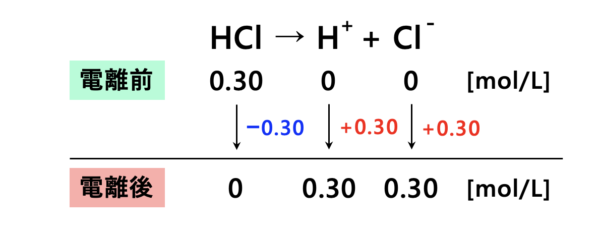
上の図を見ると、\(\rm{[H^+]=0.30\ mol/L}\)となります。

このとき、注意ポイントがあります。
それは水の電離を考える必要があるか？という点です。

 
 
それでは「② 水の電離」を考慮する必要があるかを考えていきましょう。

水のイオン積から水の電離による\(\rm{H^+}\)は\(\rm{[H^+]=1.0 × 10^{-7}\ mol/L}\)です。

この結果を整理すると、下のようになります。
① \(\rm{HCl}\)の電離：\(\rm{[H^+]=0.30\ mol/L}\)
② 水の電離：\(\rm{[H^+]=1.0 × 10^{-7}\ mol/L}\)

①と②を比較すると、明らかに②が小さいです。(① \(\gg\) ②)

 
そのため、今回は「②水の電離」を無視して

\(\rm{[H^+]=0.30+1.0×10^{-7}≒0.30\ mol/L}\)

として\(\rm{pH}\)を計算しましょう。

 
\(\rm{pH=-log_{10}[H^+]=-log_{10}0.30 = -log_{10}3+1=0.52}\)

 
答え：\(\rm{pH=0.52}\)

ここで、まず間違った解答を示します。

 
塩酸は酸性ですが、水で希釈することで塩基性になることはありません。

 
では、ここから正解を一緒に考えていきましょう。
先ほどと同様に\(\rm{HCl}\)と水の電離を考えてみましょう。

 
① \(\rm{HCl}\)の電離：\(\rm{[H^+]=1.0 × 10^{-8}\ mol/L}\) (\(1000\)倍の希釈より)
② 水の電離：\(\rm{[H^+]=1.0 × 10^{-7}\ mol/L}\) (水のイオン積より)
 
①と②を比較すると、①と②の差がほとんどないので、\((1)\)と違って②を無視できません。
そこで、\(\rm{HCl}\)の電離に加えて、水の電離も考慮していきましょう。
このように、極めて薄い酸の電離を考えるときには、水の電離も考慮する必要があります。

 
水の電離も考慮した\(\rm{pH}\)の求め方を\(3\)ステップで解説していきます。
 
① 水の電離による\(\rm{[H^+]=}\)\(x\ \rm{mol/L}\)とおく

[HClと水の電離を図として書く]

水の電離を考慮すると、
\(\rm{[H^+]=}\)\( x + 10^{-8}\ \rm{mol/L}\)
\(\rm{[OH^-]=}\)\(x\ \rm{mol/L}\)
となります。
 
② 水のイオン積を活用する
\(\rm{[H^+]}\)、\(\rm{[OH^-]}\)が表現できたので、
これを水のイオン積\(K_w = \rm{[H^+][OH^-] = 1.0×10^{-14}\ (mol/L)^2}\)に代入しましょう。

\(K_w = \rm{[H^+][OH^-]} =\)\(（x + 10^{-8}）x = 10^{-14}\ \rm{(mol/L)^2}\)

 
これを式変形すると、

\(x^2 + 10^{-8}x -10^{-14} = 0\)

と\(x\)の\(2\)次方程式になります。

 
解の公式を使うと、

\(x = \large \frac{-10^{-8} + \sqrt{10^{-16} + 4×10^{-14}}}{2}\)\(\rm{=9.5 × 10^{-8}\ mol/L}\)
(ここで、\(x\)は必ず正なので、\(\sqrt{}\)の前の符号は\(+\)にしています。)
 
③ \(\rm{[H^+]}\)から\(\rm{pH}\)を求める
\(x\)が求められたので、

\(\rm{[H^+]=9.5 ×10^{-8} + 10^{-8} =1.05 × 10^{-7}\ mol/L}\)

となります。

 
これから最後に\(\rm{pH}\)を求めていきましょう。

\(\rm{pH=-log_{10}[H^+] = log_{10}(1.05 × 10^{-7}) = 7 – log_{10}1.05 = 6.98}\)

答え：\(\rm{pH=6.98}\)

\(\rm{H_2CO_3 ⇄ H^+ + {HCO_3}^-}\)　①
\(\rm{{HCO_3}^- ⇄ H^+ + {CO_3}^{2-}}\)　②

ただし、①の電離定数\(K_1\)は\(\rm{5.0×10^{-7}\ mol/L}\)、②の電離定数\(K_2\)は\(\rm{5.0×10^{-11}\ mol/L}\)である。

 
\((1)\) \(\rm{25°C}\)の水\(\rm{1.0\ L}\)に対して、\(\rm{1.0×10^5\ Pa}\)の二酸化炭素は最大\(\rm{3.5×10^{-2}\ mol}\)溶解する。この水溶液の炭酸の電離度と、水素イオン濃度は？

\((2)\) この水溶液の炭酸イオン\(\rm{{CO_3}^{2-}}\)の濃度は？

ではここから、溶解した\(\rm{CO_2}\)の濃度を\(C\ \rm{[mol/L]}\)、第\(1\)電離の電離度を\(\alpha\)として電離定数\(K_1\)を表現していきましょう。

① 電離定数\(K_1\)を表現する

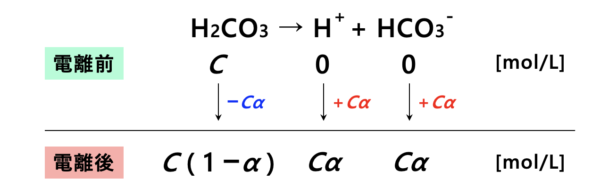
上の図から、

\(K_1 = \large \rm{\frac{[H^+][{HCO_3}^-]}{[H_2CO_3]}} \small =\) \(\large \frac{C \alpha \cdot C \alpha}{C(1 – \alpha)} \small = \large \frac{C \alpha ^2}{1 – \alpha}\)

 
② 電離定数\(\alpha \ll 1\)と近似して電離度\(\alpha\)を求める
電離度\(\alpha\)が\(\alpha \ll 1\)であるとすると、\(1 – \alpha ≒ 1\)と近似できます。

なので、
\(K_1 = C \alpha ^2\)
となり、電離度は
\(\alpha = \sqrt{\large \frac{K_1}{C}}\)
で求めることができます。

 
溶解した\(\rm{CO_2}\)の濃度は\(C=3.5×10^{-2}\ \rm{mol/L}\)なので、これを代入していきましょう。

電離度は\(\alpha = \sqrt{\large \frac{K_1}{C}} \small = \sqrt{\large \frac{5.0×10^{-7}}{3.5×10^{-2}}} \small ≒3.8×10^{-3}\)

 
③ 近似が正しかったか確認する
最後に、電離度\(\alpha \ll 1\)の近似が正しかったかを確認します。
この確認は非常に大切なので、必ずするようにしてくださいね。

 
電離度\(\alpha\)が\(0.05\)より小さいとき、近似して\(\rm{OK}\)でした。

電離度\(\alpha \leq 0.05\)というのは、水溶液中で\(5\%\)以下しか電離していないという意味です。
\(5\%\)以下、つまりほとんど電離していないので、電離度が極端に小さいと近似できるわけですね。

 
今回の場合も確認すると、電離度\(\alpha = 0.0038 \lt 0.05\)なので、この近似は\(\rm{OK}\)ですね！

 
では最後に、水素イオン濃度\(\rm{[H^+]}\)も求めておきましょう。

\(\rm{[H^+]‎ =}\)\( C \alpha =3.5 × 10^{-7} ×3.8 ×10^{-3} ≒ 1.3 × 10^{-4}\ \rm{mol/L}\)

 
答え：\(\alpha = 0.0038\)、\(\rm{[H^+]=1.3 × 10^{-4}\ mol/L}\)

この問題のポイントは以下となります。

 
それでは、\((1)\)の\(\rm{[H^+]}\)を利用して第\(2\)電離も考慮した\(\rm{[H^+]}\)を求めていきましょう。

 
第\(2\)電離で\(x\ \rm{[mol/L]}\)平衡が移動するとすると、電離平衡後は次のようになります。

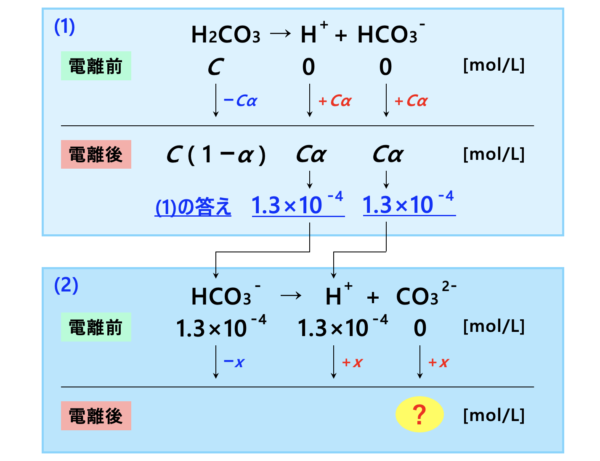
ここで、\(K_2\)は極端に小さいので、

・\(\rm{[{HCO_3}^-]=}\)\(1.3 × 10^{-4} – x≒1.3 × 10^{-4}\ \rm{mol/L}\)
・\(\rm{[H^+] ‎ =}\)\( 1.3 × 10^{-4} + x ≒ 1.3 × 10^{-4}\ \rm{mol/L} \)

として考えることができます。

 
これらを電離定数\(K_2\)の式に代入して、\(x\)を求めていきます。

\(K_2 = \large \rm{\frac{[H^+] [{CO_3}^{2-}]}{[{HCO_3}^-]}} \small =\) \(x = 5.0 ×10^{-11}\ \rm{mol/L}\)

 
よって、\(\rm{[{CO_3}^{2-}] = 5.0 ×10^{-11}\ mol/L}\)となります。

どこで近似をしてよいかをしっかりと理解してくださいね。

 
答え：\(\rm{[{CO_3}^{2-}] = 5.0 ×10^{-11}\ mol/L}\)

\((2)\) \(\rm{pH\ 1.0}\)の塩酸\(\rm{100\ mL}\)と\(\rm{pH\ 4.0}\)の塩酸\(\rm{100\ mL}\)を混合した溶液の\(\rm{pH}\)は？

まずは、それぞれの電離を考えていきます。
\(\rm{HCl}\)、\(\rm{NaOH}\)ともに電離度は\(1\)なので、次のように完全に電離します。

　　\(\rm{HCl → H^+ + Cl^-}\)

　　\(\rm{NaOH → Na^+ + OH^-}\)

 
\(\rm{H^+：0.10 × 20.0 = 2\ mmol}\)

\(\rm{OH^-：0.10 × 30.0 = 3\ mmol}\)

 
これから\(\rm{H^+}\)の\(\rm{2\ mmol}\)は\(\rm{OH^-}\)と完全に中和して、溶液中には\(\rm{OH^- = 1\ mmol}\)が残ることがわかります。
ここから、水酸化物イオン濃度\(\rm{[OH^-]}\)を求めていきます。

溶液中の\(\rm{OH^-}\)の物質量を溶液の全体量で割ると、濃度を求めることができます。

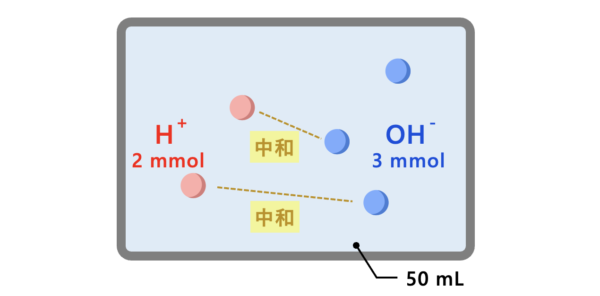
\(\rm{[OH^-] = \large \frac{1\ mmol}{50.0\ mL} \small = 2.0 × 10^{-2}\ mol/L}\)

ここから水のイオン積\(K_w ‎ = \rm{[H^+][OH^-] = 1.0×10^{-14}\ (mol/L)^2}\)を使って、\(\rm{[H^+]}\)を求めていきましょう。

\(\rm{[H^+] ‎ = }\)\(\large \frac{K_w}{\rm{[OH^-]}} \small = \large \frac{1.0×10^{-14}}{2.0 × 10^{-2}} \small = \large \frac{1}{2} \small ×10^{-12}\ \rm{mol/L}\)

 
よって、

\(\rm{pH = -log_{10} \left(\large \frac{1}{2} \small ×10^{-12} \right) = 12 + \log_{10}2 = 12.3}\)

となります。

 
答え：\(\rm{pH=12.3}\)

この問題のポイントも\((1)\)とまったく同じです。
今回は、塩基がないので、それぞれの\(\rm{H^+}\)の物質量を考えていきましょう。

 
・\(\rm{pH\ 1.0}\)の塩酸の\(\rm{H^+}\)：
\(\rm{pH\ 1.0}\)のとき、\(\rm{[H^+]‎ = 10^{-1}\ mol/L}\)なので、

\(\rm{H^+}\)：\(\rm{10^{-1} × 100 = 10\ mmol}\)

 
・\(\rm{pH\ 4.0}\)の塩酸の\(\rm{H^+}\)：
\(\rm{pH\ 4.0}\)のとき、\(\rm{[H^+]‎ = 10^{-4}\ mol/L}\)なので、

\(\rm{H^+}\)：\(\rm{10^{-4} × 100 = 10^{-2}= 0.010\ mmol}\)

 
以上から、溶液を混合すると、

\(\rm{H^+}\)の\(\rm{mol}\)：\(\rm{10 + 0.010 = 10.010\ mmol}\)

溶液の量：\(\rm{100 + 100 = 200\ mL}\)

 
よって、
\(\rm{[H^+] ‎ =  \large \frac{10.010}{200} \small = 0.0501 ≒ 0.050\ mol/L}\)

\(\rm{pH =- log_{10}0.050 = -log_{10}(2^{-1} × 10^{-1}) = 1 + log_{10}2 = 1.3}\)

 
答え：\(\rm{pH=1.3}\)