
- \(\rm{{H_2CO_3}^*}\)の考え方
- ヘンリーの法則
を特にポイントとしています.昨日の自分より少しでもレベルアップしていきましょう!
解説してほしい分野があればぜひ次の記事のコメント欄で教えてくださいね!

炭酸
炭酸は水に二酸化炭素が溶け込むことで生じます.炭酸(\(\rm{H_2CO_3}\))はテストなどで頻出ですが,問題になると難しいと感じてしまう方が多い分野でもあります.
そこで,今回は炭酸の電離平衡について解説していき,テストでもよく出る問題についてもわかりやすく解説していきます.この記事を読むことで,炭酸の電離平衡の苦手意識を払拭していきましょう!
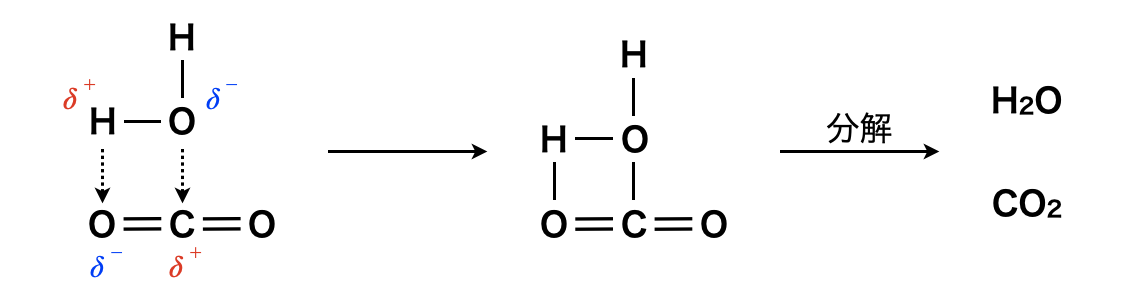
炭酸の電離を理解するためには,まず炭酸を理解する必要があります.\(\rm{CO_2}\)は無極性分子ですが,下の図のように部分的に極性をもつので,若干ですが水に溶けます.その一部が図のように反応して,炭酸\(\rm{H_2CO_3}\)を生じます.ただ,\(\rm{H_2CO_3}\)は水溶液中のみに存在する弱酸で,ある濃度以上になると,必ず\(\rm{CO_2}\)と\(\rm{H_2O}\)に分解されます.
炭酸の電離平衡
気体の二酸化炭素を水に溶かすと,二酸化炭素は水中で分子状態である\(\rm{CO_2(aq)}\)となって溶解して平衡状態となります.
\(\rm{CO_2(g)\ ⇄\ CO_2(aq)}\)
さらにこの\(\rm{CO_2(aq)}\)が水分子と反応することで,炭酸\(\rm{H_2CO_3}\)に変化して平衡状態となります.
\(\rm{CO_2(aq)\ +\ H_2O\ ⇄\ H_2CO_3}\)
この反応の平衡定数は\(\rm{K = 1.7 × 10^{-3}}\)なので,著しく左に偏っています.そのため水溶液中の二酸化炭素の大部分は\(\rm{CO_2}\)分子として存在していることがわかります.
そしてこの炭酸(\(\rm{H_2CO_3}\))から\(\rm{H^+}\)が\(2\)段階電離することで,以下のような電離平衡が生じます.
\(\rm{H_2CO_3\ ⇄\ H^+\ +\ {HCO_3}^-}\)
\(\rm{{HCO_3}^-\ ⇄\ H^+\ +\ {CO_3}^{2-}}\)
ここで厳密に考えていきましょう.
\(\rm{CO_2(aq)}\)と\(\rm{H_2CO_3}\)を識別することは困難であるため,\(\rm{CO_2(aq)}\)と\(\rm{H_2CO_3}\)をまとめて\(\rm{{H_2CO_3}^*}\)と表すことにします.ここがテストで初見であれば難しい点であるため,しっかりと理解してくださいね!すると,炭酸(\(\rm{H_2CO_3}\))の\(2\)段階電離は以下のように書き換えることができます.
\(\rm{{H_2CO_3}^*\ ⇄\ H^+\ +\ {HCO_3}^-}\)
\(\rm{{HCO_3}^-\ ⇄\ H^+\ +\ {CO_3}^{2-}}\)
ここで水溶液中の\(\rm{{H_2CO_3}^*}\)の濃度を求める方法も解説していきましょう.二酸化炭素を水に溶かすため,\(\rm{Henry}\)の法則を使うことができます.\(\rm{Henry}\)の法則については以下の記事をご覧ください.

すると,\(\rm{CO_2}\)の分圧\(p_{\rm{CO_2}}\)を用いて,以下のように表すことができます.
\({\rm{[{H_2CO_3}^*]}}\ =\ k × p_{\rm{CO_2}}\)
\(k\)は\(\rm{Henry}\)定数です.ここまで理解したところで,以下の問題を解いてみましょう!
実践力を養おう!
水に気体の二酸化炭素を溶かすと,以下のような平衡状態を形成する.
\(\rm{CO_2(g)\ ⇄\ CO_2(aq)}\) (\(1\))
\(\rm{CO_2(aq)\ +\ H_2O\ ⇄\ H_2CO_3}\) (\(2\))
そして式(\(2\))で生じた\(\rm{H_2CO_3}\)は以下のように一部が電離する.
\(\rm{H_2CO_3\ ⇄\ H^+\ +\ {HCO_3}^-}\) (\(3\))
\(\rm{{HCO_3}^-\ ⇄\ H^+\ +\ {CO_3}^{2-}}\) (\(4\))
式(\(3\)),(\(4\))の電離定数を\(K_1\),\(K_2\)とすると,それぞれ以下のように表される.
\(K_1 = \large \rm{\frac{[H^+] [{HCO_3}^-]}{[H_2CO_3]}}\),\(K_2 = \large \rm{\frac{[H^+] [{CO_3}^{2-}]}{[{HCO_3}^-]}}\)
ただし,水溶液中の\(\rm{CO_2(aq)}\)と\(\rm{H_2CO_3}\)を識別することはできないため,これらの濃度をまとめて\(\rm{[{H_2CO_3}^*]}\)と表し,式(\(3\))を以下のように書き直し,そのときの電離定数を\({K_1}^*\)とした.
\(\rm{{H_2CO_3}^*\ ⇄\ H^+\ +\ {HCO_3}^-}\) (\(3\))\(’\)
\({K_1}^* = \large \rm{\frac{[H^+] [{HCO_3}^-]}{[{H_2CO_3}^*]}}\)
今回の考慮する温度では,\({K_1}^* = 4.5 × 10^{-7}\ \rm{mol/L}\),\(K_2 = 4.7 × 10^{-11}\ \rm{mol/L}\)である.
(\(1\))式(\(2\))について溶媒である\(\rm{H_2O}\)の濃度はほぼ一定と考えることができるため,それを考慮して電離定数を\(K_0\)とするとどのように表すことができるか?
(\(2\))気体の\(\rm{CO_2}\)を\(\rm{1.0 × 10^5\ Pa}\)下で純水と接して放置すると,平衡状態になった.\(\rm{[{H_2CO_3}^*]}\),\(\rm{[H^+]}\),\(\rm{[{CO_3}^{2-}]}\)の値はいくらになるか?このとき,\(\rm{[{H_2CO_3}^*]}\)の濃度には\(\rm{Henry}\)の法則が成り立つとし,\(\rm{Henry}\)定数\(k\)は,\(k = 3.2 × 10^{-7}\ \rm{mol/(L \cdot Pa)}\)とする.
(\(3\))\(K_1\)を\(K_0\)と\({K_1}^*\)を用いて表せ.
(\(4\))(\(1\))で求めた\(K_0\)の値が\(1.8 × 10^{-3}\)であったとする.(\(2\))の条件下で考えると,\(\rm{[H_2CO_3]}\)の値はいくらになるか?
このように\(\rm{{H_2CO_3}^*}\)が問題に出てきたとしてもしっかりと対応できるようにしておきましょう!とても詳しく解説していきます.
(\(1\))
問題文にも書かれているように,\(\rm{H_2O}\)の濃度はほぼ一定なので,考慮しなくて\(\rm{OK}\)です.これは炭酸に限らずなので,しっかりと覚えておいてくださいね!
\(K_0 = \rm{\large \frac{[H_2CO_3]}{[CO_2(aq)]}}\)
(\(2\))
順に求めていきましょう.
・\(\rm{[{H_2CO_3}^*]}\)
\(\rm{[{H_2CO_3}^*]}\)については,\(\rm{CO_2}\)が\(\rm{H_2O}\)に溶けるときに,\(\rm{Henry}\)の法則を用いて濃度を考えます.
\({\rm{[{H_2CO_3}^*]}} = k × p_{\rm{CO_2}} = (3.2 × 10^{-7}) × (1.0 × 10^5) = 3.2 × 10^{-2}\ \rm{mol/L}\)
・\(\rm{[H^+]}\)
式(\(3\))\(’\)と式(\(4\))の電離定数を考えます.
\({K_1}^* = 4.5 × 10^{-7}\ \rm{mol/L}\),\(K_2 = 4.7 × 10^{-11}\ \rm{mol/L}\)より,\(K_2\)が圧倒的に小さいので式(\(4\))の電離は無視することができます.式(\(3\))\(’\)の電離だけを考えると,\(\rm{[H^+] = [{HCO_3}^-]}\)と考えることができます.
\({K_1}^* = \large \rm{\frac{[H^+] [{HCO_3}^-]}{[{H_2CO_3}^*]} \small = \large \frac{[H^+]^2}{[{H_2CO_3}^*]}}\)
この式に\(\rm{[{H_2CO_3}^*] = 3.2 × 10^{-2}\ mol/L}\)を代入すると,\(\rm{[H^+]}\)を求めることができます.
\({\rm{[H^+]}} = \sqrt{{K_1}^* × \rm{[{H_2CO_3}^*]}} = \sqrt{(4.5 × 1^{-7}) × (3.2 × 10^{-2})} = 1.2 × 10^{-4}\ \rm{mol/L}\)
・\(\rm{[{CO_3}^{2-}]}\)
今回の問題では,\(\rm{[H^+] = [{HCO_3}^-]}\)と考えることができるので,これを\(K_2\)に代入して求めていきます.
\(K_2 = \large \rm{\frac{[H^+] [{CO_3}^{2-}]}{[{HCO_3}^-]} \small = [{CO_3}^{2-}] = 4.7 × 10^{-11}\ mol/L}\)
(\(3\))
\(K_1\)を\(K_0\)と\({K_1}^*\)を用いて表します.このような式変形が苦手な方も多いですので,今回でポイントをしっかりとおさえてくださいね!
ポイント\(1:\)まず求めるものを書く
ポイント\(2:\)消去する文字を見極める
ポイント\(3:\)整理する
この順でやっていきましょう!
ポイント\(1:\)まず求めるものを書く
今回の求めるものは\(K_1\)なので,\(K_1\)の式を書きます.
\(K_1 = \large \rm{\frac{[H^+] [{HCO_3}^-]}{[H_2CO_3]}}\)
ここで,\(\rm{[{H_2CO_3}^*] = [H_2CO_3] + [CO_2(aq)]}\)を使ってさらに式変形をしていきます.
\(K_1 = \large \rm{\frac{[H^+] [{HCO_3}^-]}{[{H_2CO_3}^*]\ -\ [CO_2(aq)]}}\)
ポイント\(2:\)消去する文字を見極める
今回は\(\rm{[{H_2CO_3}^*]}\),\(\rm{[CO_2(aq)]}\)を消去します.
\({\rm{[{H_2CO_3}^*]}} = \large \frac{{\rm{[H^+] [{HCO_3}^-]}}}{{K_1}^*}\)
\({\rm{[CO_2(aq)]}} = \large \frac{1}{K_0} \small × {\rm{[H_2CO_3]}} = \large \frac{1}{K_0} \small × \large \frac{{\rm{[H^+] [{HCO_3}^-]}}}{K_1} \small = \large \frac{{\rm{[H^+] [{HCO_3}^-]}}}{K_0K_1}\)
ポイント\(3:\)整理する
消去する文字を代入していきます.
\(K_1 = \large \frac{{\rm{[H^+] [{HCO_3}^-]}}}{\frac{{\rm{[H^+] [{HCO_3}^-]}}}{{K_1}^*}\ -\ \frac{{\rm{[H^+] [{HCO_3}^-]}}}{K_0K_1}} \small = \large \frac{1}{\frac{1}{{K_1}^*}\ -\ \frac{1}{K_0K_1}}\)
\(K_1 \left( \large \frac{1}{{K_1}^*}\ \small -\ \large \frac{1}{K_0K_1} \small \right) = 1\)
\(\large \frac{K_1}{{K_1}^*}\ \small -\ \large \frac{1}{K_0} \small = 1\)
\(K_1 = {K_1}^* \left( 1 + \large \frac{1}{K_0} \right)\)
今回この式変形の問題を取り上げたのは,苦手な方が多いためです.私は基本的にこの\(3\)ステップで解いていますので,ぜひみなさんも練習問題などで力をつけてくださいね!
(\(4\))
今回は(\(2\))の条件下における\(\rm{[H_2CO_3]}\)を求めます.(\(2\))の条件下とは,\(\rm{[H^+] = [{HCO_3}^-]}\)ということです.(\(3\))から\(\rm{[H_2CO_3]}\)がわかるのは,\(K_1\)の式ですね.
\({\rm{[H_2CO_3]}} = \large \frac{{\rm{[H^+] [{HCO_3}^-]}}}{K_1} \small = {\rm{[H^+]^2}} × \large \frac{K_0}{{K_1}^*(1\ +\ K_0)}\)
ここまでで式変形は完了です.これに値を代入していきます.
\({\rm{[H_2CO_3]}} = (1.2 × 10^{-4})^2 × \large \frac{1.8\ ×\ 10^{-3}}{4.5\ ×\ 10^{-7}\ ×\ (1\ +\ 1.8 × 10^{-3})} \small = 5.7 × 10^{-7}\ \rm{mol/L}\)
この問題はかなり難易度が高く,\(\rm{{H_2CO_3}^*}\)という考え方を理解できているかどうかがカギとなります.
難関大を攻略する上では重要な知識なのでしっかりと理解できるようにしておいてくださいね!



コメント