
この分野は対策が手薄になりがちなので,
ここでしっかりと学習しておきましょう!
今回は理論についての理解を深めていきます!
今日も頑張りましょうー!
反応速度の定義
反応速度の定義についてみていきましょう!
まず,下の反応があるとします.
\(\rm{A\ +\ 2B\ →\ C\ +\ D}\)
化学反応では時間の進行とともに,反応物(反応式の左側)が減少し,生成物(反応式の右側)が増加します.
そのときの反応速度について考えていきましょう!
\(\rm{A}\)が\(\Delta t\)の間に\(\ \Delta [\rm{A}]\)だけ減少したとします.(\(\Delta\)については下に解説してあります!)
すると,\(\rm{A}\)の減少速度は下のようになります.
\(v_{\rm{A}}\ =\ \large \frac{\Delta [\rm{A}]}{\Delta t}\)
\(\ \Delta [\rm{A}]\)は\(\rm{A}\)の濃度を表しています.ここで注意するポイントは,上の式は「\(\rm{A}\)の減少速度」であるという点です.なぜかというと,\(\rm{A}\)は減少しているため\(\Delta [\rm{A}]\)はマイナスの値になります.\(\Delta t\)はプラスなので,\(v_{\rm{A}}\)はマイナスとなります.
化学の分野だけでなく物理や数学においても,この\(\Delta\)という記号を非常によく使用しますので,ここでしっかりと覚えてしまいましょう!
\(\Delta\)とは,「変化量」のことです.
変化量とは,ある物質がどれほど変化したのかということです.
計算方法は次のように考えてください.
\(\Delta A\ =\ A_{after}\ -\ A_{before}\)
このように,\(\Delta\)計算では(後)ー(前)をするということをしっかりと覚えておいてくださいね!
ここで,速度には\(2\)種類あります.
平均の反応速度と瞬間の反応速度です.
平均の反応速度
平均の反応速度は,先ほど説明したものです.
\(\bar v_{\rm{A}}\ =\ -\ \large \frac{\Delta [\rm{A}]}{\Delta t}\)
ここで,大切なのは「\(-\)」をつけることです.速度というときには基本的に「プラス」になるように考えます.
そのため,便宜的に「\(-\)」をつけて考えています.
一方で,\(\rm{C}\)の生成速度を考えてみましょう.
\(\rm{C}\)の生成速度は\(\Delta [\rm{C}]\ >\ 0\)であるので,マイナスをつける必要はありません.
そのため
\(\bar v_{\rm{C}}\ =\ \large \frac{\Delta [\rm{C}]}{\Delta t}\)
となります.
速度についてマイナスをつけるかどうかは,その時々によります.
覚えるのでなく,状況によって自分で考えられるようになることが大切です!
瞬間の反応速度
瞬間の反応速度は,下のようになります.
\(v\ =\ -\ \lim_{\Delta t \to 0} \large \frac{\Delta [\rm{A}]}{\Delta t}\ \small =\ – \large \frac{d[\rm{A}]}{dt}\)
式で考えると難しいので,グラフで平均の反応速度と瞬間の反応速度の違いを考えていきましょう!
それぞれの反応速度はグラフの傾きとなります.

平均の反応速度について,時間\(t_1,t_2\)の間での反応速度となります.
一方で瞬間の反応速度は,時刻\(t_1,t_2\)という時間によってそれぞれ反応速度が異なります.
これが上の式の微分という意味です.
反応速度と濃度の関係
以前の記事で.反応速度を変化させるには,濃度・温度・活性化エネルギーを変化させる必要があると説明しました.
【基礎から丁寧に】反応速度ってどうやって決まるの?その要因は?
今回は,その中でも最も大きなファクターである濃度について考えていきます.
以下の反応を例にして反応速度を考えていきましょう.
\(\rm{A\ +\ 2B\ →\ C\ +\ D}\)
以前も紹介しましたが,反応が生じるためには粒子同士が衝突する必要があります.
衝突は一般に濃度に比例するはずなので,\([\rm{A}]\)について比例するはずです.
同様のことは\(\rm{B}\)についてもいえるので,反応速度は\([\rm{A}][\rm{B}]\)に比例するはずです.
次に,\(\rm{A}\)と\(\rm{B}\)が衝突して,\(\rm{A_1}\)と\(\rm{C}\)が発生し,\(\rm{A_1}\)と\(\rm{B}\)が衝突して,\(\rm{C}\)と\(\rm{D}\)が発生するという反応が起こる可能性もあります.
つまり,\(\rm{A}\ 1\)個と\(\rm{B}\ 2\)個が\(\ 1\)回の反応でちょうど反応して,\(\rm{C}\)と\(\rm{D}\)が発生するという確率は非常に低いです.
この場合,\(\rm{A,A_1,…}\)などをそれぞれ区別するのではなく,\([\rm{A}]\)として表すために,下のように反応速度を表します.
\(v_{\rm{A}}\ =\ k\ [{\rm{A}}]^x\ [{\rm{B}}]^y\)
ここで,注意ポイントがあります.
これらの係数は実験を通して,経験的に決まるものです.
ですので後ほど説明しますが,実験データなどが与えられ\(x,y\)を決定していくようになります!
\(x\ =\ 1\)のとき,一次反応,\(x\ =\ 2\)のとき,二次反応といいます!
上の反応式の中の比例定数\(k\)を「反応速度定数」といいます.反応速度定数\(k\)は,温度に依存する定数となっています.
つまり温度が一定であれば,\(k\)の値は一定になるということです.
ここで,\(v_{\rm{A}}\)についてまとめてみましょう.
今まで説明したように,\(v_{\rm{A}}\)を表すためには,\(2\)通りがありました.
\(v_{\rm{A}}\ =\ k\ [{\rm{A}}]^x\ [{\rm{B}}]^y\)
\(v_{\rm{A}}\ =\ -\ \large \frac{d[{\rm{A}}]}{dt}\)
これを\(v_{\rm{A}}\)についてまとめると,以下のようになります.
\( -\ \large \frac{d[{\rm{A}}]}{dt}\ \small =\ k\ [{\rm{A}}]^x\ [{\rm{B}}]^y\)
これを微分方程式を呼びます.
ここから下は大学の範囲となるため,理解できる必要はありませんが,流れはおさえておくと他の受験生に差をつけられますよ!
簡単のために,ここでは\(x\ =\ 1,y\ =\ 0\)のときを考えてみましょう!
\(-\ \large \frac{d[{\rm{A}}]}{dt}\ \small =\ k\ [{\rm{A}}]\)
\(\large \frac{d[{\rm{A}}]}{[{\rm{A}}]}\ \small =\ -\ kdt\)
\(\large \int \frac{1}{[{\rm{A}}]}\ \small d[{\rm{A}}]\ =\ -\ \large \int kdt\)
\(\log[{\rm{A}}]\ =\ -\ kt\ + C\ \) \(C\):積分定数
\(C\)を求める必要があります.ここで考えるのが初期条件です.
初期条件:\([{\rm{A}}]\ =\ [{\rm{A}}]_0\ {\rm{at}}\ t\ =\ 0\)
この初期条件を上の式に代入します.すると,
\(C\ =\ \log[\rm{A}]_0\)
よって,
\(\log[{\rm{A}}]\ =\ -\ kt\ +\ \log[{\rm{A}}]_0\)
と求めることができます!
途中の式変換は難しいので,微分方程式の詳細は後日記事にしますね!
最後に,これを\([{\rm{A}}]\)についてグラフを考えてみましょう!
\([{\rm{A}}]\ =\ [{\rm{A}}]_0\ \times \ e^{-kt}\)
となり,グラフは下のようになります.
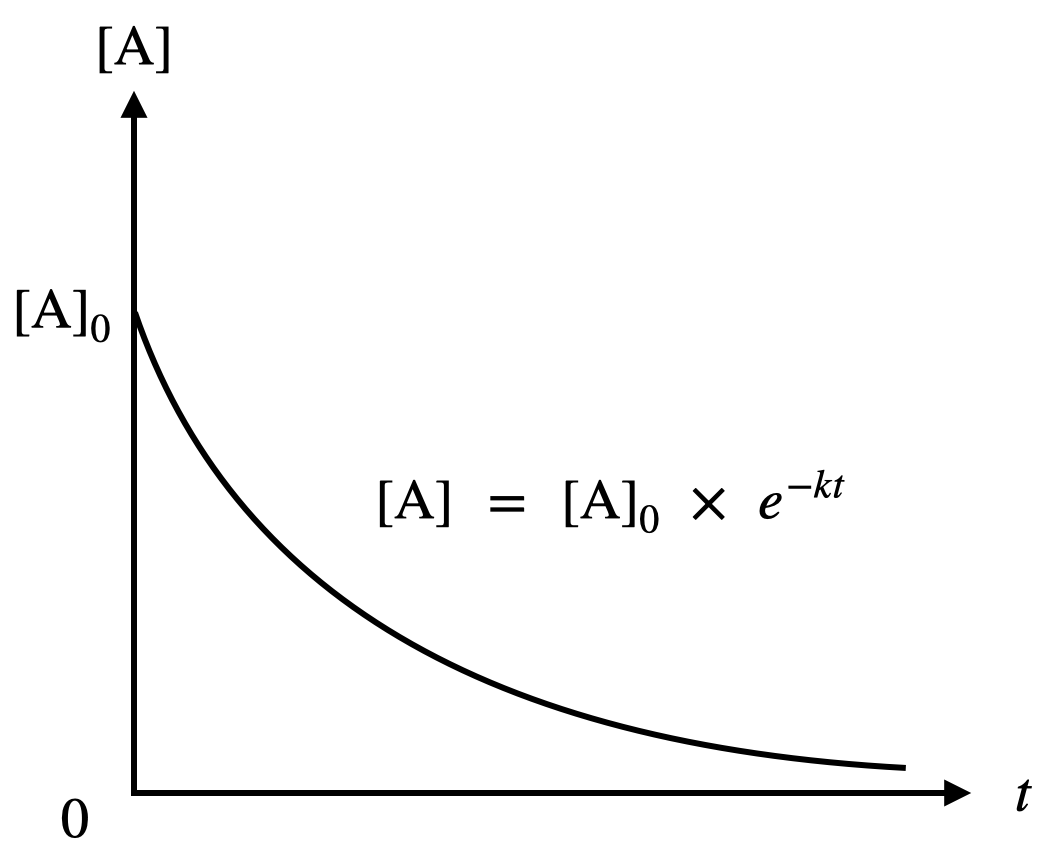
このグラフを見ると,反応の進行によって物質Aの濃度が少しずつ減少していることがわかります.
これは直感と一致していますね!



コメント