今回のメニューです。
✅シャルルの法則
✅アボガドロの法則
✅気体の状態方程式
✅気体定数\(R\)
今回の記事を読んでいただくと、気体の状態方程式について完全理解することができます。
最後まで丁寧に解説していくので、ぜひ最後までご覧ください!
また、わからないことはぜひコメント欄までお願いします。
解説してほしい分野があればぜひ次の記事のコメント欄で教えてくださいね!

私はYouTubeでも高校化学の解説をしているので、ぜひそちらもご覧ください。
はじめに
今回は気体の性質について学んでいきましょう。
気体を考えるときの重要な変数は\(3\)つあります。
それは圧力、体積、温度です。
これらの\(3\)つの値が決まることで、気体の状態が\(1\)つに決定されます。
ここで 気体の性質を考えるときに重要な要素があります。
それが「理想気体」と「実在気体」です。
実際の分子には、分子間力や分子の体積が存在しています。
しかしながら、これらの値を\(0\)として理想状態を考えるのが、理想気体になります。
今回はまず基本として理想気体について解説していきます。
実在気体についてはこちらの記事で徹底解説してますので、ぜひご覧ください!

\(P\)、\(V\)、\(T\)とは?
ある容器の中に気体の分子を入れてみましょう。
すると気体は乱雑に運動しています。
この運動の性質を表現するのが、圧力、体積、温度になります。
\(P:Pressure\)
まずは圧力についてです。
圧力は英語で\(Pressure\)なので、記号は\(P\)、単位は\(\rm{Pa}\)で表されます。
圧力とは気体分子が容器に衝突したとき、その壁が単位面積あたりに受ける力のことをいいます。
\(V:Volume\)
次は体積についてです。
体積は英語で\(Volume\)なので、記号は\(V\)、単位は\(\rm{L}\)で表されます。
気体の体積とは、気体分子自身の体積ではなく、気体分子の動ける空間の大きさをいいます。
なので、この図でいうと容器の体積がつまり\(V\)になります。
\(T:Temperature\)
最後は温度についてです。
温度は英語で\(Temperature\)なので、記号は\(T\)で表されます。
この温度\(T\)は、気体分子の熱運動の激しさを表します。
つまり気体分子のもつ平均運動エネルギー\(\large \frac{1}{2} \small mv^2\)は
式変形をすると\(\large \frac{3}{2} \small kT\)と表されるので、温度の関数であることがわかります。
ここで温度の単位に注意する必要があります。
温度の単位は\(\rm{°C}\)ではなく、\(\rm{K}\)(ケルビン)を使います。
この\(T\)\(\rm{\ [K]}\)は通常の温度\(t\)\(\rm{\ [°C]}\)に\(\rm{273°C}\)を足したものになります。
この温度\(T\)のことを絶対温度といいます。
絶対温度については、この後のシャルルの法則の部分で解説しますね!
ボイルの法則
ある気体を下のような箱の中に入れて、温度が一定の状態でピストンをゆっくりと上から押していくとします。
このときの圧力\(P\)と体積\(V\)の関係をグラフで見ていきましょう。
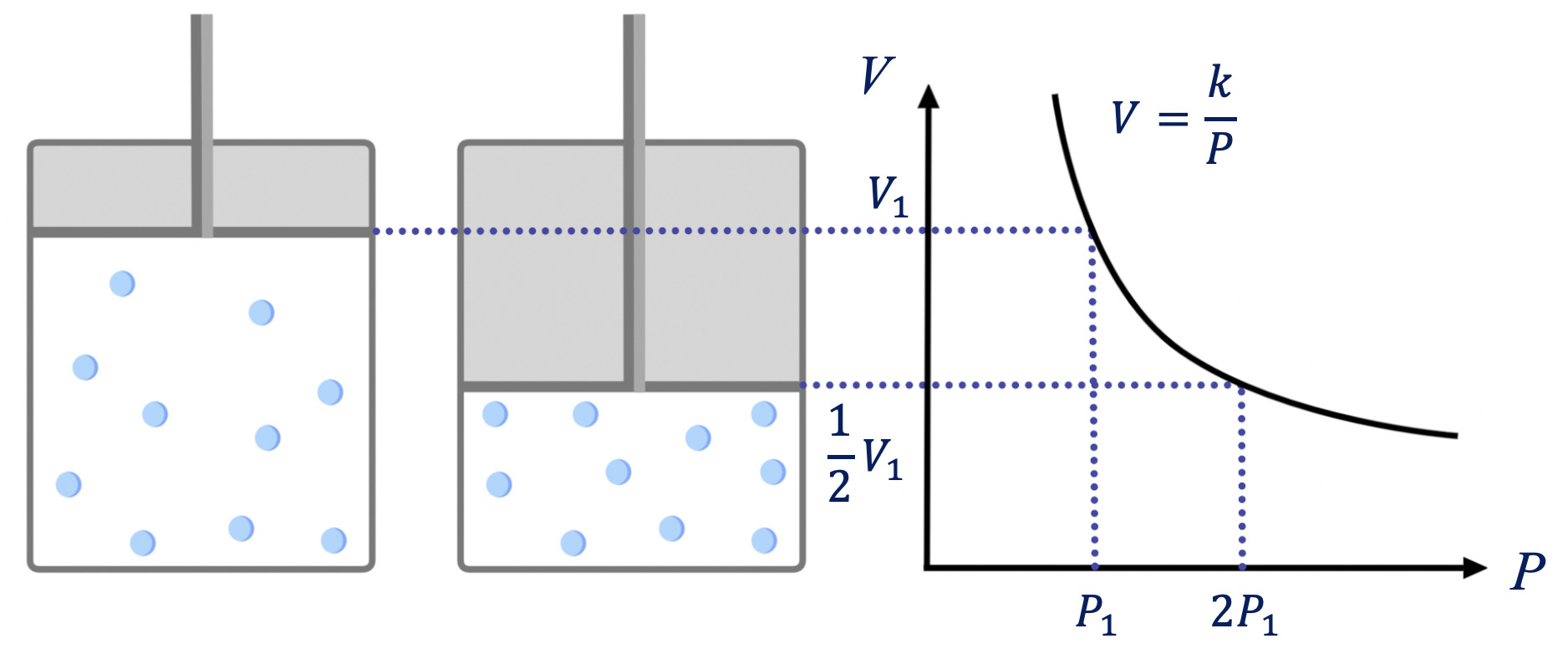
上から加える圧力をどんどん大きくしていくと、体積は小さくなっていきます。
このとき、圧力を\(2\)倍にすると気体の体積は\(\large \frac{1}{2}\)倍になります。
つまり、このグラフを見ると温度が一定であれば、
\(V = \large \frac{k}{P}\)
が成り立つので、気体の体積\(V\)は圧力\(P\)に反比例することがわかります。
これを発見した人にちなんでボイルの法則といいます。
\(V = \large \frac{k}{P}\)
シャルルの法則
先ほどのボイルの法則は、圧力\(P\)と体積\(V\)の関係でした。
次は温度\(T\)と体積\(V\)の関係を見ていきましょう。
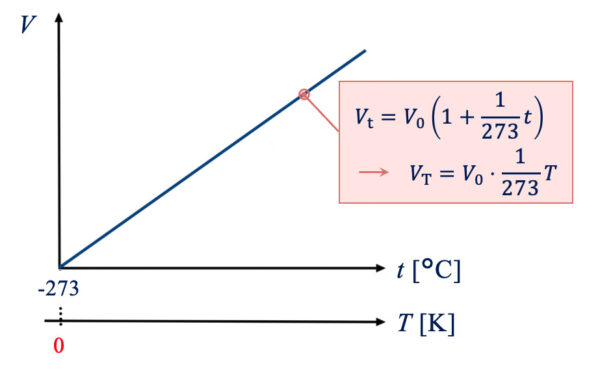
\(\rm{0°C}\)での気体の体積を\(V_\rm{0}\)、\(t\ \rm{°C}\)での気体の体積を\(V_\rm{t}\)とすると、 下のような関係があり、
どの気体でも、\(\rm{1°C}\)あたりの膨張係数がほぼ\(\large \frac{1}{273}\)であることがわかりました。
\(V_{\rm{t}} = V_{\rm{0}} \left ( \small 1 + \large \frac{1}{273} \small t \right )\)
この式を見ると、体積がマイナスになることはないので、
\(1 + \large \frac{1}{273} \small t=0\)
つまり、\(t=-273 \rm{°C}\)で\(V_{\rm{t}}=0\)になることがわかります。
この体積が\(0\)となる温度を\(0\)として絶対温度として扱うようになりました。
これを絶対温度\(\ T\ \)(大文字)と呼びます。
この絶対温度を使うと、先ほどの式は下のように書き換えられます。
\(V_{\rm{t}} = V_{\rm{0}} \left ( 1+ \large \frac{1}{273} \small t \right)\)
\(\ \ \ = V_{\rm{0}} \left ( 1 + \large \frac{1}{273} \small (T-273) \right)\)
\(\ \ \ = \large \frac{V_{\rm{0}}}{273} \small T\)
ここで\(\large \frac{V_0}{273}\)は定数なので、
\(V_{\rm{t}} = kT\)
となります。
\(V = kT\)
アボガドロの法則
次は、アボガドロの法則です。
アボガドロの法則とは、「同数の分子を含む気体は、同温・同圧下では、同じ体積である」というものです。
これも図を書いて、考えていきましょう。
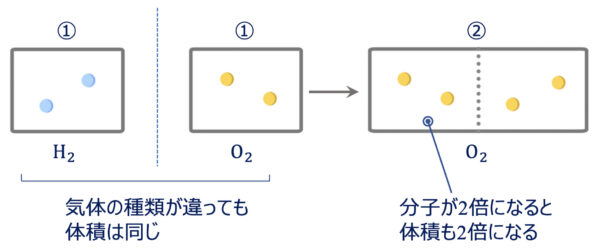
ここで、\(\rm{H_2}\)分子と\(\rm{O_2}\)分子を考えてみましょう。
\(\rm{H_2}\)、\(\rm{O_2}\) \(\rm{\ 1\ mol}\)同士とすると、アボガドロの法則から同じ体積になります。
そして、\(\rm{O_2}\)分子を\(\rm{2\ mol}\)にすると、体積は先ほどの\(2\)倍になります。
つまり、気体の体積は、容器内の物質量(モル)によって決まることがわかります。
なので、同温・同圧下では、気体の体積はその中に含まれる気体の物質量\(\rm{[mol]}\)に比例するので、
\(V=kn\)
となります。
気体の状態方程式の導出
では、今までに学んだ各法則を使って、気体の状態方程式を導いてみましょう。
ここで、状態1から状態2への変化を考えてみます。
そのために、状態1→状態3→状態4→状態2のルートで気体の状態を考えていきましょう。
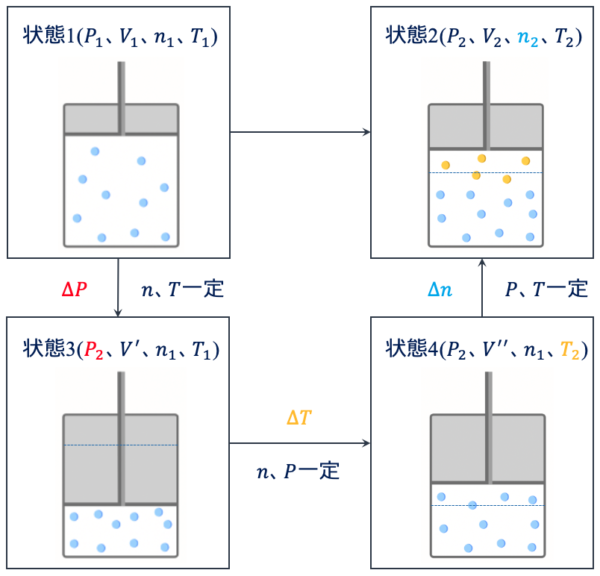
まず、状態1から状態3への変化は、\(n\)、\(T\)が一定なので、ボイルの法則が成り立ちます。
\(P_1 V_1 =P_2 V^{’} ・・・①\)
次に、状態3から状態4への変化は、\(n\)、\(P\)が一定なので、シャルルの法則が成り立ちます。
\(\large \frac{V^{’}}{T_1} \small = \large \frac{V^{’’}}{T_2} \small ・・・②\)
最後に、状態4から状態2への変化は、\(P\)、\(T\)が一定なので、アボガドロの法則が成り立ちます。
他の物質を容器内に入れたというイメージです。
\(\large \frac{V^{’’}}{n_1} \small = \large \frac{V_2}{n_2} \small ・・・③\)
この①~③式から、\(V^{’}\)、\(V^{’’}\)を消去していきます。
まず、①式から\(V^{’}\)を消去して、
\(V^{’} = \large \frac{P_1}{P_2} \small V_1\)
次に、③式から、\(V^{’’}\)を消去します。
\(V^{’’} = \large \frac{n_1}{n_2} \small V_2\)
これらの式を②式に代入していきます。
\(\large \frac{1}{T_1} \left ( \frac{P_1}{P_2} \small V_1 \right ) = \large \frac{1}{T_2} \left ( \frac{n_1}{n_2} \small V_2 \right )\)
これを式変形すると、
\(\large \frac{P_1 V_1}{n_1 T_1} \small = \large \frac{P_2 V_2}{n_2 T_2}\)
となります。
これを見ると、\(\large \frac{PV}{nT}\)は常に一定であることがわかります。
そしてこの定数を\(R\)とすると、
\(PV=nRT\)
となり、参考書でよく見る気体の状態方程式となります。
一連の式変形からわかるように、気体はどんな状態変化をさせたとしても気体の状態方程式で表すことができます。
そのため、気体の問題では、気体の状態方程式を使って、あらゆる問題を解くように練習していきましょう!
気体定数\(R\)
では、状態方程式の気体定数についてみていきましょう。
標準状態(\(\rm{0°C}\)、\(\rm{1.0×10^5\ Pa}\))での気体分子\(\rm{1\ mol}\)の体積は、気体の種類に関係なく常に\(\rm{22.4\ L}\)なので、
これらの値を気体の状態方程式に代入して気体定数\(R\)の値を求めてみましょう。
ここで、温度は絶対温度なので、\(\rm{273\ K}\)となることに注意してくださいね。
\(R = \large \frac{PV}{nT} \small = \large \frac{1.0×10^5\ \rm{Pa}\ ×\ 22.4\ \rm{L}}{1\ \rm{mol}\ ×\ 273\ \rm{K}} \small = 8.31×10^3\ \rm{Pa\ L/(mol\ K)}\)
ここで、圧力というのは、単位面積あたりに働く力なので、\(\rm{Pa = \large \frac{N}{m^2}}\)と変形できます。
そして、\(\rm{J}\)は\(\rm{N×m}\)です。
なので、これらの関係を使っていくと、気体定数の単位は、下のように変形できます。
\(\rm{\large \frac{Pa\ L}{mol\ K} \small = \large \frac{\frac{N}{m^2} m^3}{mol\ K} \small = \large \frac{J}{mol\ K}}\)
\(\rm{8.31×10^3\ J/(mol\ K)}\)は単位含めてしっかりと覚えておこう!
まとめ
では、最後に気体の状態方程式のまとめをしておきましょう。
理想気体の状態を扱うときには、常に\(PV=nRT\)が成り立ちます。
なので、この式を使って、気体の状態変化に関する問題を解いていきましょう。
そして、\(PV=nRT\)の気体定数であるRの値はテストで聞かれることもあるので、
単位も合わせて\(R=8.31×10^3\ \rm{J/(mol\ K)}\)としっかりと覚えておきましょう。
私はYouTubeでも高校化学の解説をしているので、ぜひそちらもご覧ください。



コメント