
京都大学は難しい問題が多いと言われますが,その分多くのことを学ぶことができます.
各問題で,1つでも多くの知識を習得していきましょう!
大問1の総評
初めまして,こんにちは.KUTです.
本記事では,徹底解説シリーズとして2020年京大化学の大問1について解説していきます.
また解説に加えて,それぞれの問題で覚えておいてほしいポイントについて詳しく説明していきます.
京大の化学は難しいという印象が強い方が多いと思いますが,京大化学には難しい問題と標準問題の2つがあります.ここで,受験生が対策すべきことが2つあります.
1つ目は,標準問題を最後まで解き切る力を身につけることです.これにより,まずは平均点を取ることを目指します.
2つ目は,難しい問題と標準問題を見分けられる目を養うことです.試験本番は時間制限内に自分の解ける問題を解き切る必要があります.そのため,難しい問題は解かずに,標準問題をしっかりと選択していきながら,最後まで解いていくことが必要になります.
この記事では,問題を選択していく目を養うために,どのようにして判断していくのかということも自分なりに説明していきます.
京都大学の化学は基本的に穴埋め問題が中心です.この穴埋め問題をクリアできるかどうかが鍵となります.穴埋め問題ということは,前後の文章により誘導があるということです.この誘導を味方にできるかが重要になります.
2020年大問1については,
(a):電離平衡・溶解度積
この問題は標準的なので,しっかりと理解してほしい問題です.
(b):結晶構造
結晶構造として,閃亜鉛鉱型構造・ウルツ鉱型構造を考える問題でした.この問題は普段はあまり学習したことがないため,難しい問題でした.
それでは,2020年京大化学の大問1の解説に進んでいきましょう!
大問1(a)解説
本問題は,\(2\)段階電離を考慮するとともに,溶解度積を考える問題です.
まず\(2\)段階電離の問題では,それぞれの平衡反応を比較することが重要になります.
今回の問題について考えていきましょう!
\(\rm{H_2S\ ⇄\ H^+\ +\ HS^-}\) \(\ K_{\rm{a1}}\ =\ 1.0\ ×\ 10^{-7}\ \rm{mol/L}\)
\(\rm{HS^-\ ⇄\ H^+\ +\ S^{2-}}\) \(K_{\rm{a2}}\ =\ 1.0\ ×\ 10^{-14}\ \rm{mol/L}\)
\(K_{\rm{a1}},K_{\rm{a2}}\)を比較すると,
\(\large \frac{K_{\rm{a1}}}{K_{\rm{a2}}} \small = \large \frac{1.0\ ×\ 10^{-7}}{1.0\ ×\ 10^{-14}}\ \small =\ 1.0 × 10^7\)
これは\(K_{\rm{a1}}\)の方が\(K_{\rm{a2}}\)より\(10^7\)倍大きい,つまり第\(1\)電離の方が第\(2\)電離よりも\(10^7\)倍起きやすいという意味です.そのため,第\(2\)電離について無視することができます.
第\(2\)電離の反応はほとんど起こらず,\(\rm{HS^-}\)由来の\(\rm{H^+}\)はほとんど生成されないということです.
問題文にも以下のような記述があります.
これは今説明したような内容を意味しています.
過去問を解く解くときには,このように問題を解くだけでなく,その周辺の知識も増やしていきましょう!
それでは,これらを踏まえた上で問題を解いていきましょう!
ア
先ほどの説明したように,第\(1\)電離についてのみ考えればよいです.
平衡が\(x\ \rm{mol/L}\)移動するとすると,下のようになります.

それぞれの平衡後の濃度を電離定数の式に代入することで,\(x\)を求めることができます.
\(K_{\rm{a}} = \large \frac{x\ ×\ x}{0.1\ -\ x} \small = 1.0 × 10^{-7}\)
一般的にこの分母:\(0.1\ -\ x\)については近似して\(0.1\)とすることができます.ここの考え方については下のポイントにまとめています.
\(x = \sqrt{1.0 × 10^{-7} × 0.1} = 1.0 × 10^{-4}\ \rm{mol/L}\)
よって,
\(\rm{pH} =\ – \log{[H^+]} =\ – \log{(1.0 × 10^{-4})} = 4\)
となります.
みなさん,ほとんどの場合近似して計算していると思います.
しかしながら近似計算を行うためには,当然近似できる条件があります.それが,
全体:\(\rm{[H^+] = 100 : 5}\)以下
というものです.
これは溶液全体に対して\(\rm{[H^+]}\)(今回の問題では\(x\ \rm{mol/L}\))がどれだけ存在しているか,ということであり,\(5 \%\)以下であれば\(\rm{OK}\)ということです.
これを今回の問題について考えてみましょう.
溶液全体は\(0.1\ \rm{mol/L}\)であるため,
全体:\(\rm{[H^+] = 0.1 : 1.0 × 10^{-4} = 100 : 0.1}\)
となります.そのため今回は近似計算を行うことができます.
毎回,この確認を行うだけで平衡問題を根本からしっかりと理解することができますよ!
また,\(\rm{pH}\)についても一応確認しておきましょう.
\(\rm{pH}\)を求める式は下のようになります.これは必ず覚えてくださいね!
\(\rm{pH} =\ – \log{[H^+]}\)
これについて式変形をすると,\(\rm{[H^+] = 10\ -\ pH}\)となります.\(\rm{pH}\)が\(1\)大きくなると,\(\rm{[H^+]}\)は\(\large \frac{1}{10}\)倍となり,\(2\)大きくなると,\(\rm{[H^+]}\)は\(\large \frac{1}{100}\)倍となります.そのため\(\log\)を使って表しています.
イ
次に,\(\rm{[S^{2-}]}\)について求めていきましょう.
ここでも重要なポイントがあります.
\(2\)段階電離の問題ではそれぞれの電離定数である\(K_{\rm{a1}},K_{\rm{a2}}\)の積をとり,\(\rm{[HS^-]}\)を消去していきます.
\(K_{\rm{a1}} \cdot K_{\rm{a2}} \rm{= \large \frac{[H^+][HS^-]}{[H_2S]} \small × \large \frac{[H^+][S^{2-}]}{[HS^-]} \small = \large \frac{[H^+]^2[S^{2-}]}{[H_2S]} \small = 1.0 × 10^{-21}\ (mol/L)^2}\)
この式に\(\rm{[H_2S]}\)と\(\rm{[H^+]}\)のデータを代入すると,\(\rm{[S^{2-}]}\)を求めることができます.
これは\(2\)段階電離の問題の常套手段なのでしっかりと覚えておきましょう!
今回の問題では,常に硫化水素の濃度は\(1.0 × 10^{-1}\ \rm{mol/L}\)であるとしているので,
\(\large \frac{(1.0 × 10^{-1})^2\ ×\ \rm{[S^{2-}]}}{1.0 × 10^{-1}} \small = 1.0 × 10^{-21}\)
\(\rm{[S^{2-}]\ =\ 1.0 × 10^{-14}\ mol/L}\)
ウ
次は溶解度積の問題です.
溶解度積については下のようなグラフを書いて考えることで簡単に解くことができます.
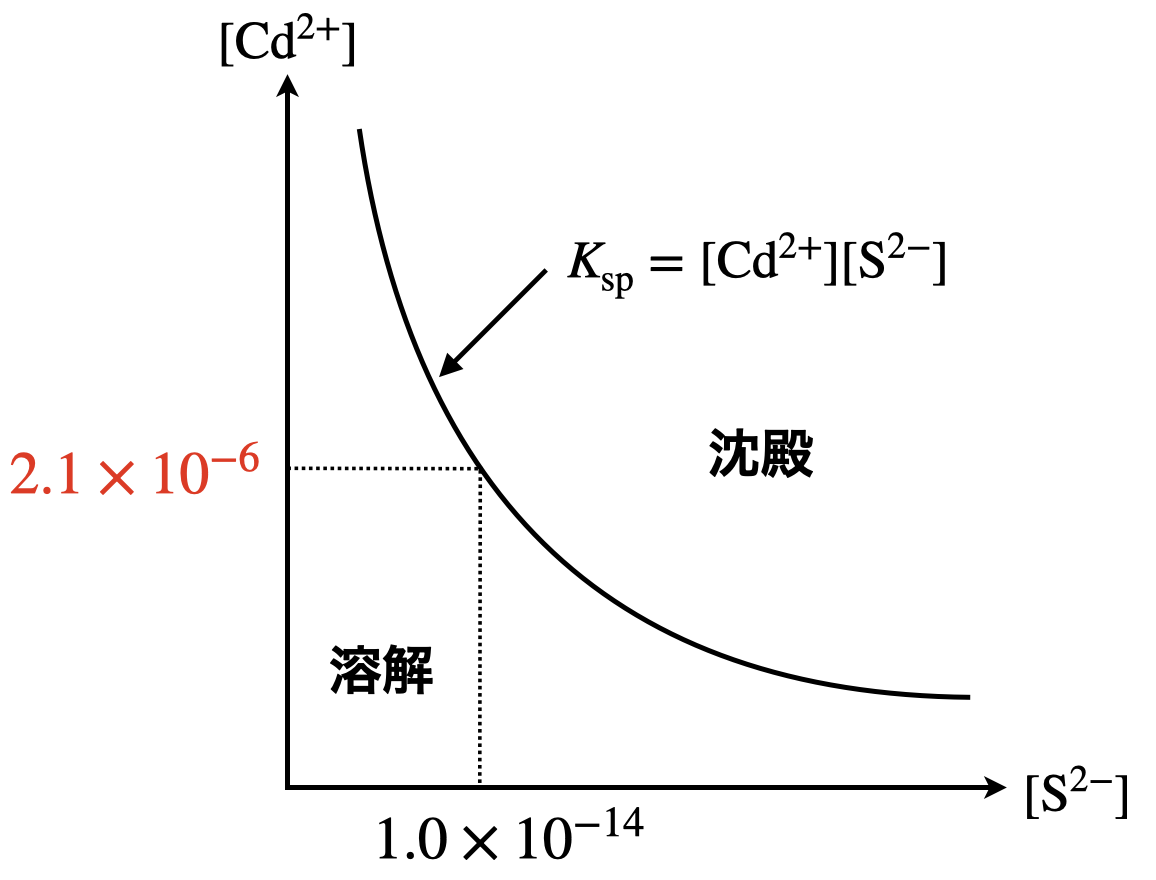
この図より,硫化カドミウムが沈殿し始めるのは
\(\rm{[Cd^{2+}]\ =\ \large \frac{2.1 × 10^{-20}}{1.0 × 10^{-14}} \small = 2.1 × 10^{-6}\ mol/L}\)
となります.
溶解度積を考えるときは,先ほども説明したように,グラフを書いて考えるようにしましょう.今回の問題で考えると,溶解度積は次のような式で表されます.
\(K_{\rm{sp}}\ =\ \rm{[Cd^{2+}][S^{2-}]\ =\ 2.1 × 10^{-20}\ (mol/L)^2}\)
この式をグラフとして考えてみましょう.縦軸を\(\rm{[Cd^{2+}]}\)(陽イオン),横軸を\(\rm{[S^{2-}]}\)(陰イオン)とすると反比例のグラフとなります.
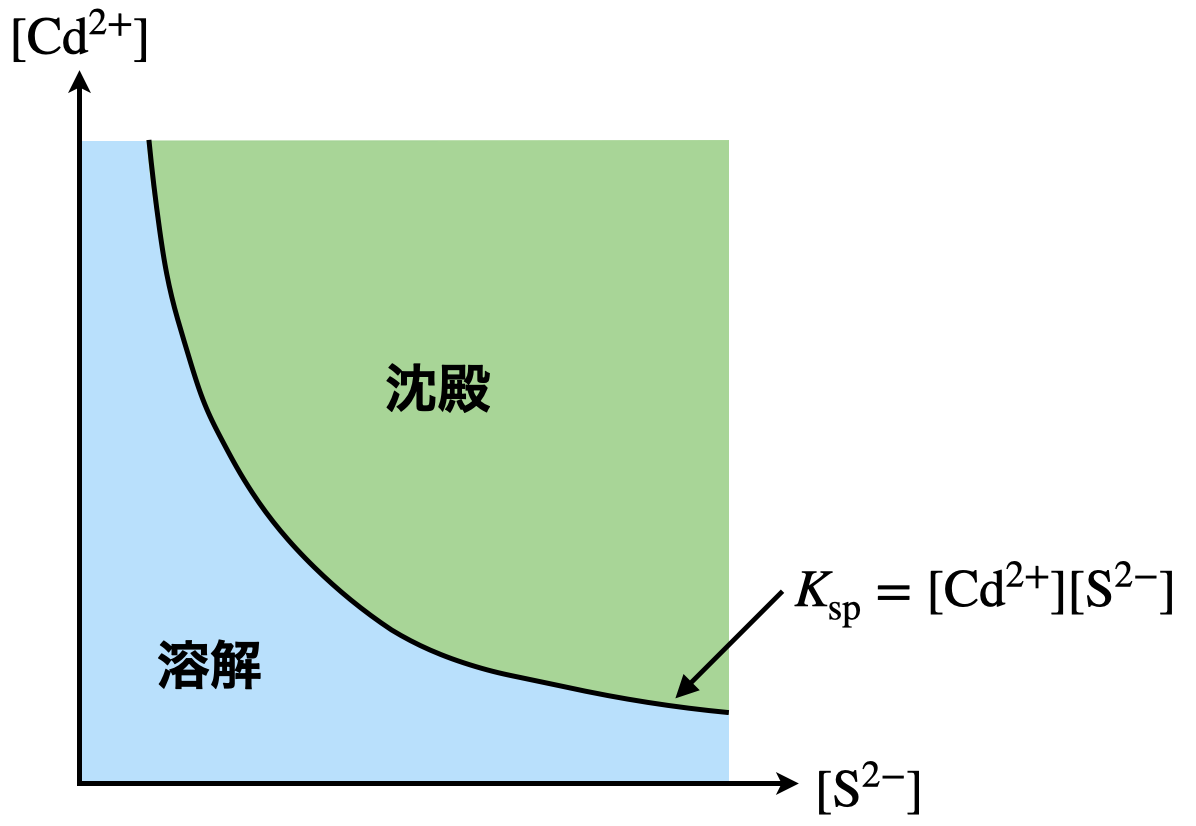
エ,オ
次は,\(\rm{pH\ =\ 7}\)の溶液について先ほどと同じように考えていきましょう.
水素イオン濃度\(\rm{[H^+]\ =\ 1.0 × 10^{-7}\ mol/L}\)であるため,
\(K_{\rm{a1}} \cdot K_{\rm{a2}} \rm{= \large \frac{[H^+]^2[S^{2-}]}{[H_2S]} \small = 1.0 × 10^{-21}\ (mol/L)^2}\)
を用いて\(\rm{[S^{2-}]}\)を求めましょう.
\(\large \frac{(1.0\ ×\ 10^{-7})^2\ ×\ \rm{[S^{2-}]}}{1.0\ ×\ 10^{-1}}\ \small =\ 1.0\ ×\ 10^{-21}\)
\(\rm{[S^{2-}]\ =\ 1.0 × 10^{-8}\ mol/L}\)
次に,オについては\(\rm{pH\ =\ 7}\)のときの溶解度積を求めます.
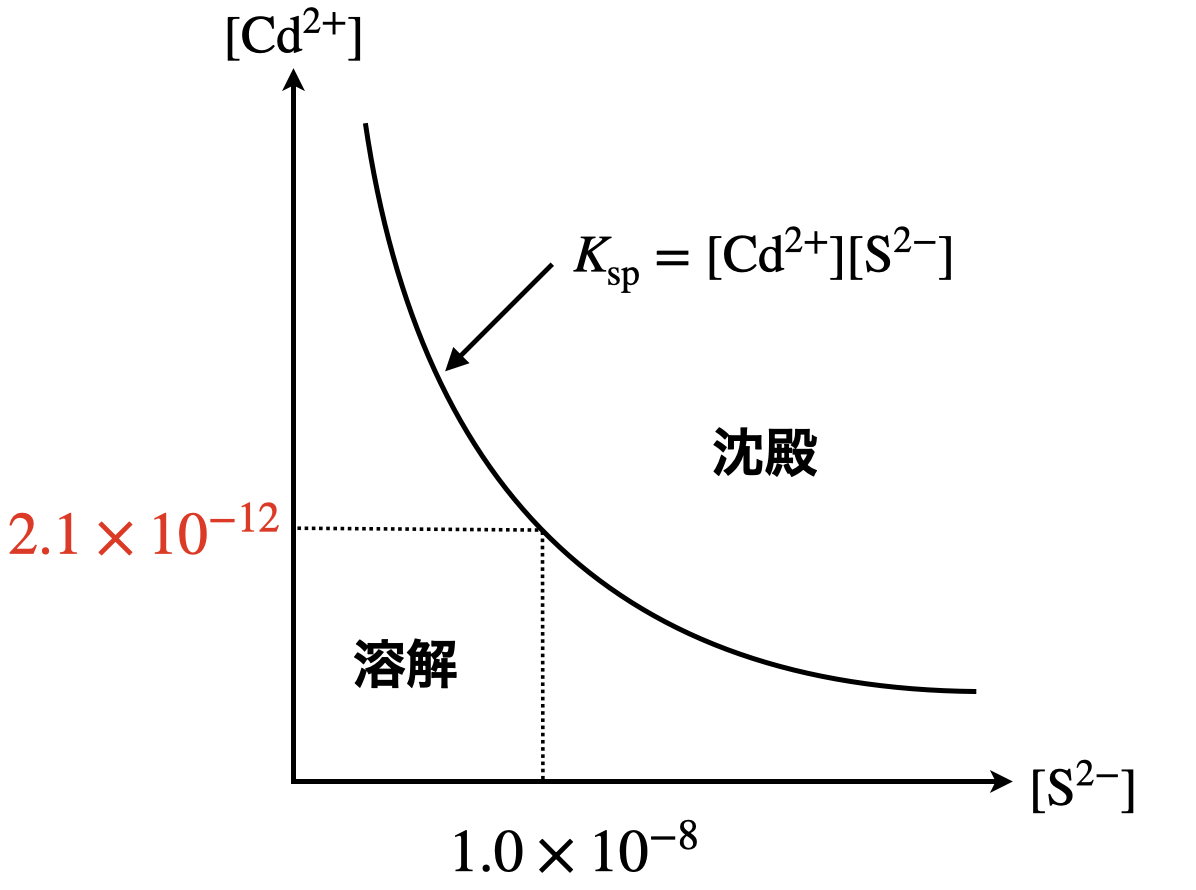
\(\rm{[Cd^{2+}]\ =\ \large \frac{2.1 × 10^{-20}}{1.0 × 10^{-8}} \small = 2.1 × 10^{-12}\ mol/L}\)
カ,キ,ク,ケ
カ〜ケについては単純に式変形をして,それぞれの四角に当てはまる数値を求めていきます.
今回考えている溶液が\(\rm{pH}\ =\ 14\)なので,水のイオン積を用いると,\(\rm{[OH]\ =\ 1.0\ mol/L}\)(すなわち\(\rm{pOH\ =\ 0}\))となります.
\(\rm{[[Cd(OH)]^+]}\ =\ K_{\rm{b1}} \rm{[Cd^{2+}][OH^{-}] = 1.4 × 10^4\ ×\ 1.0\ ×\ [Cd^{2+}]\ =\ 1.4 × 10^4 [Cd^{2+}]}\)
\(\rm{[Cd(OH)_2]}\ =\ K_{\rm{b2}} \rm{[[Cd(OH)]^+][OH^-] = 1.7 × 10^4\ ×\ 1.4 × 10^4\ [Cd^{2+}] × 1.0\ =\ 2.4 × 10^8 [Cd^{2+}]}\)
\(\rm{[[Cd(OH)_3]^-]}\ =\ K_{\rm{b3}} \rm{[Cd(OH)_2][OH^-] = 1.0 × 2.38 × 10^8 [Cd^{2+}] × 1.0 = 2.4 × 10^8 [Cd^{2+}]}\)
\(\rm{[[Cd(OH)_4]^{2-}]}\ =\ K_{\rm{b4}} \rm{[[Cd(OH)_3]^-][OH^-] = 1.0 × 2.38 × 10^8 [Cd^{2+}] × 1.0 = 2.4 × 10^8 [Cd^{2+}]}\)
水のイオン積については知っている方がほとんどでしょうが,ここで復習しておきましょう.
水のイオン積とは,水の電離平衡について考えています.
\(\rm{H_2O\ ⇄\ H^+\ +\ OH^-}\)
\(K\ =\ \large \rm{\frac{[H^+][OH^-]}{[H_2O]}}\)
水の電離度はかなり小さいので,水のモル濃度である\(\rm{[H_2O]}\)はほぼ一定であると考えることができます.そのため両辺に\(\rm{[H_2O]}\)をかけると下のようになります.
\(K_{\rm{w}}\ =\ K \rm{[H_2O] = [H^+][OH^-]}\)
この新たな定数\(K_{\rm{w}}\)を水のイオン積と読んでいます.
ここで水のイオン積と言われると,
\(K_{\rm{w}}\ =\ \rm{[H^+][OH^-] = 1.0 × 10^{-14}\ (mol/L)^2}\)
と覚えている方が多いと思いますが,これは\(25^\circ \rm{C}\)での値となります.温度が高くなると水のイオン積が少しずつ大きくなるということを覚えておいてください!
この理由について簡単に触れておきましょう.
水の反応については下のような吸熱反応となります.
\(\rm{H_2O\ =\ H^+\ +\ OH^-\ -\ 56.5\ kJ}\)
そのため,高温になるほどルシャトリエの原理により右(吸熱方向)へ平衡が移動するため,水の電離が起こりやすくなります.そのため,\(K_{\rm{w}}\)の値が大きくなります.
しかしながら,普通の問題では\(K_{\rm{w}}\ =\ 1.0 × 10^{-14}\ \rm{(mol/L)^2}\)として問題ありません.
今回の問題では,\(25^\circ \rm{C}\)と問題の初めの方に明記されていますね.
コ
水溶液中のカドミウム濃度について考えていきましょう.
水溶液中に含まれる全ての\(\rm{Cd}\)は,\(\rm{Cd^{2+},[Cd(OH)]^+,Cd(OH)_2,[Cd(OH)_3]^-,[Cd(OH)_4]^{2-}}\)のいずれかの形に変化して存在しています.そのため,以下の物質量保存則が成り立ちます.
\(\rm{[Cd]_{total} = [Cd^{2+}] + [[Cd(OH)]^+] + [Cd(OH)_2] + [[Cd(OH)_3]^-] + [[Cd(OH)_4]^{2-}]}\)
保存則とは,反応や変化の前後で総量が変化しないという法則です.化学に出てくる保存則には物質量保存則と電気量保存則があります.今回は物質量保存則について説明します.例として,\(\rm{AH}\)(例えば,\(\rm{CH_3COOH}\))の電離について考えてみましょう.\(\rm{AH}\)は以下のように電離し,平衡状態になります.
\(\rm{AH\ ⇄\ A^-\ +\ H^+}\)
この場合,電離前に\(\rm{AH}\)が\(5\ \rm{mol}\)あり,\(2\ \rm{mol}\)分電離したとすると,以下のような図に表すことができます.この中の\(\rm{AH\ 3\ mol}\)については,電離していないということです.
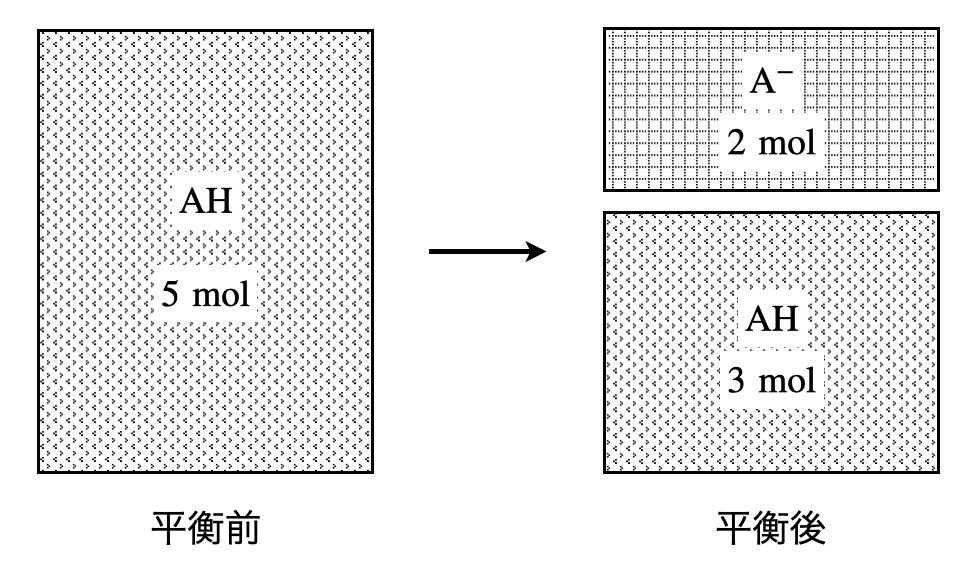
ここで,物質量保存則について考えてみましょう.
水溶液中に含まれる全ての\(\rm{A}\)は,\(\rm{AH,A^-}\)のいずれかの形に変化して存在しています.そのため,
\(\rm{[A]_{total}\ =\ [AH]\ +\ [A^-]}\)
と表すことができます.
化学についてもわかりにくい部分は簡単な例を考えて理解していきましょう!
あとは上の式に先程のカ〜ケで求めた式を代入していきましょう!
\(\rm{[Cd]_{total} =\ [Cd^{2+}] + 1.4 × 10^4 [Cd^{2+}] + 2.38 × 10^8 [Cd^{2+}] + 2.38 × 10^8 [Cd^{2+}] + 2.38 × 10^8 [Cd^{2+}]}\)
\(=7.1 × 10^8 \rm{[Cd^{2+}]}\)
サ
\(\rm{pH}\ =\ 14\)の溶液について考えていきます.
問題文より硫化水素濃度\(\rm{[H_2S]}\)は無視できるという記述から,第\(2\)電離のみ考えればよいことがわかります.
\(K_{\rm{a2}}\ =\ \rm{\large \frac{[H^+][S^{2-}]}{[HS^-]}\ \small =\ 1.0\ ×\ 10^{-14}\ mol/L}\)
このとき\(\rm{pH}\ =\ 14\),つまり\(\rm{[H^+]\ =\ 1.0 × 10^{-14}\ mol/L}\).これを代入すると,\(\rm{[HS^-]\ =\ [S^{2-}]}\)であることがわかります.
次に,\(\rm{S}\)の物質量保存則について考えてみましょう.
水溶液中に含まれる全ての\(\rm{S}\)は,\(\rm{H_2S,HS^-,S^{2-}}\)のいずれかの形に変化して存在しています.そのため以下の式が成り立ちます.
\(\rm{[S]_{total}\ =\ [H_2S] + [HS^-] + [S^{2-}]}\)
今回は\(\rm{[H_2S] ≒ 0}\)と近似できるので,
\(\rm{[S]_{total}\ =\ [HS^-] + [S^{2-}]\ = 1.0 × 10^{-1}}\)
\(\rm{[S^{2-}]\ =\ [HS^-]\ =\ 5.0 × 10^{-2}\ mol/L}\)
シ,ス
まず,\(\rm{pH}\ =\ 14\)のときの溶解度積を求めます.
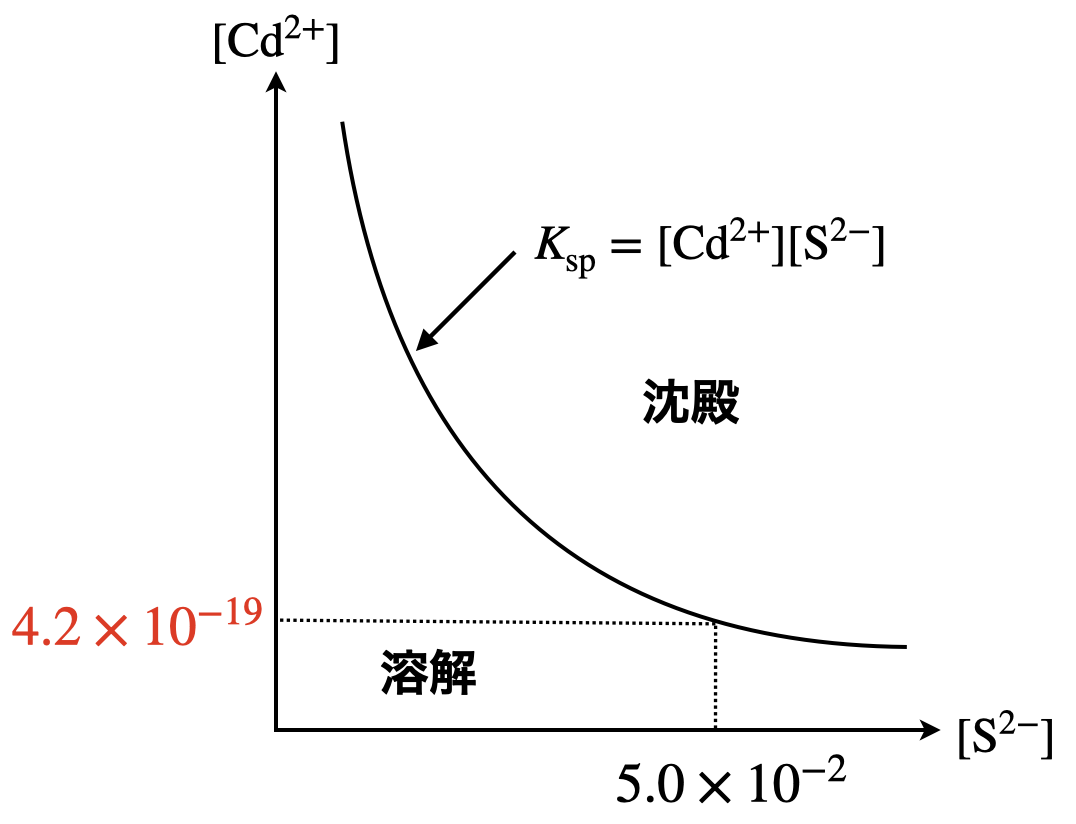
これより,
\(\rm{[Cd^{2+}]\ =\ \large \frac{2.1 × 10^{-20}}{5.0 × 10^{-2}} \small = 4.2 × 10^{-19}\ mol/L}\)
となります.
\(\rm{[Cd]_{total}\ = 7.14 × 10^8\ [Cd^{2+}] = 7.14 × 10^8 × 4.2 × 10^{-19} = 3.0 × 10^{-10}\ mol/L}\)
この結果より,\(\rm{pH}\)を高くすると,溶液中に溶解する\(\rm{Cd^{2+}}\)の濃度は小さくなることがわかります.
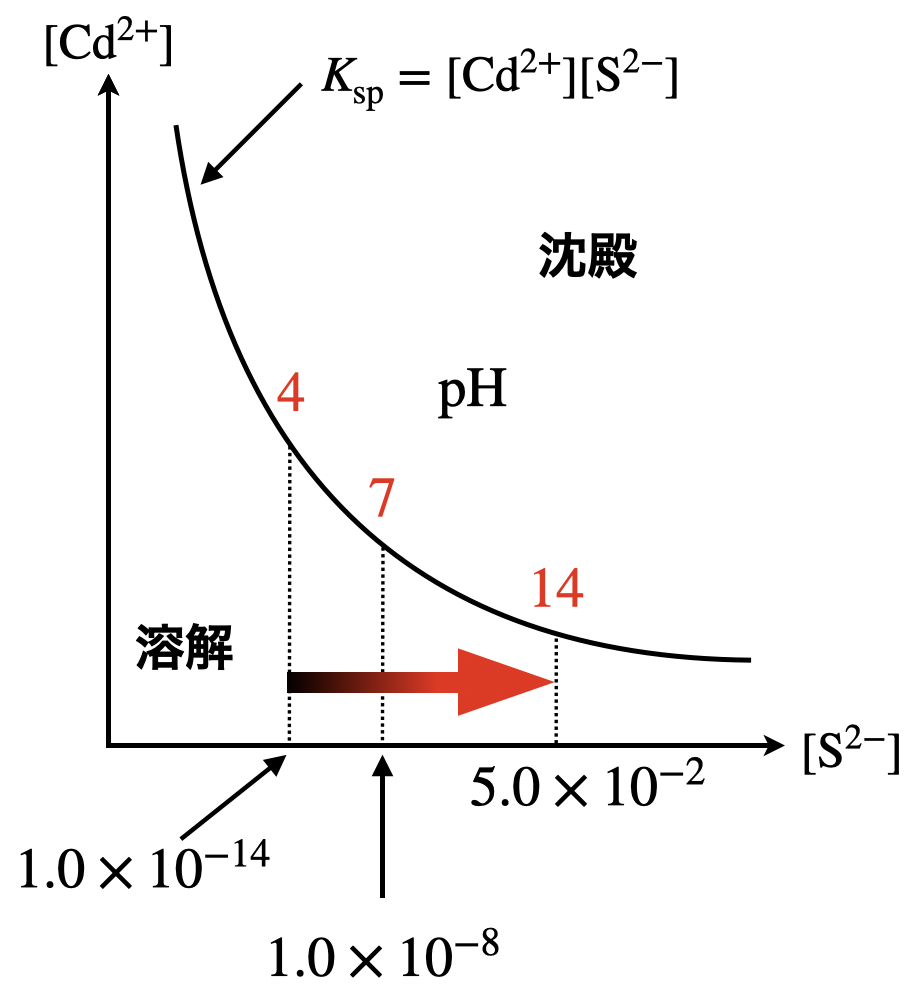
過去問を解いて,このような気づきにまで考えられるようになると問題を俯瞰的に見る力が養えますよ!

大問\(1(\rm{a})\)のみでこんなに長くなってしまいました…笑
この勢いのまま,大問\(1(\rm{b})\)に進んでいきますよ!
大問1(b)解説
次に,大問\(1(\rm{b})\)を解説していきましょう.
本問題は結晶構造に関する問題です.全体的に難易度が高い問題となっており,解けなくても問題はありません.解説を読んでいきながら,少しずつ自分ものにしていってくださいね!
それでは問題文を読んでいきましょう!
問2
あ
問題を読んだだけでは,八面体間隙・四面体間隙についてのイメージがつきにくいと思いますので,ここで説明しておきましょう.
最密構造の\(1\)つである面心立方格子の球と球の間には\(2\)種類の隙間があります.\(4\)個の球に囲まれた隙間を四面体間隙,\(8\)個の球に囲まれた隙間を八面体間隙といいます.
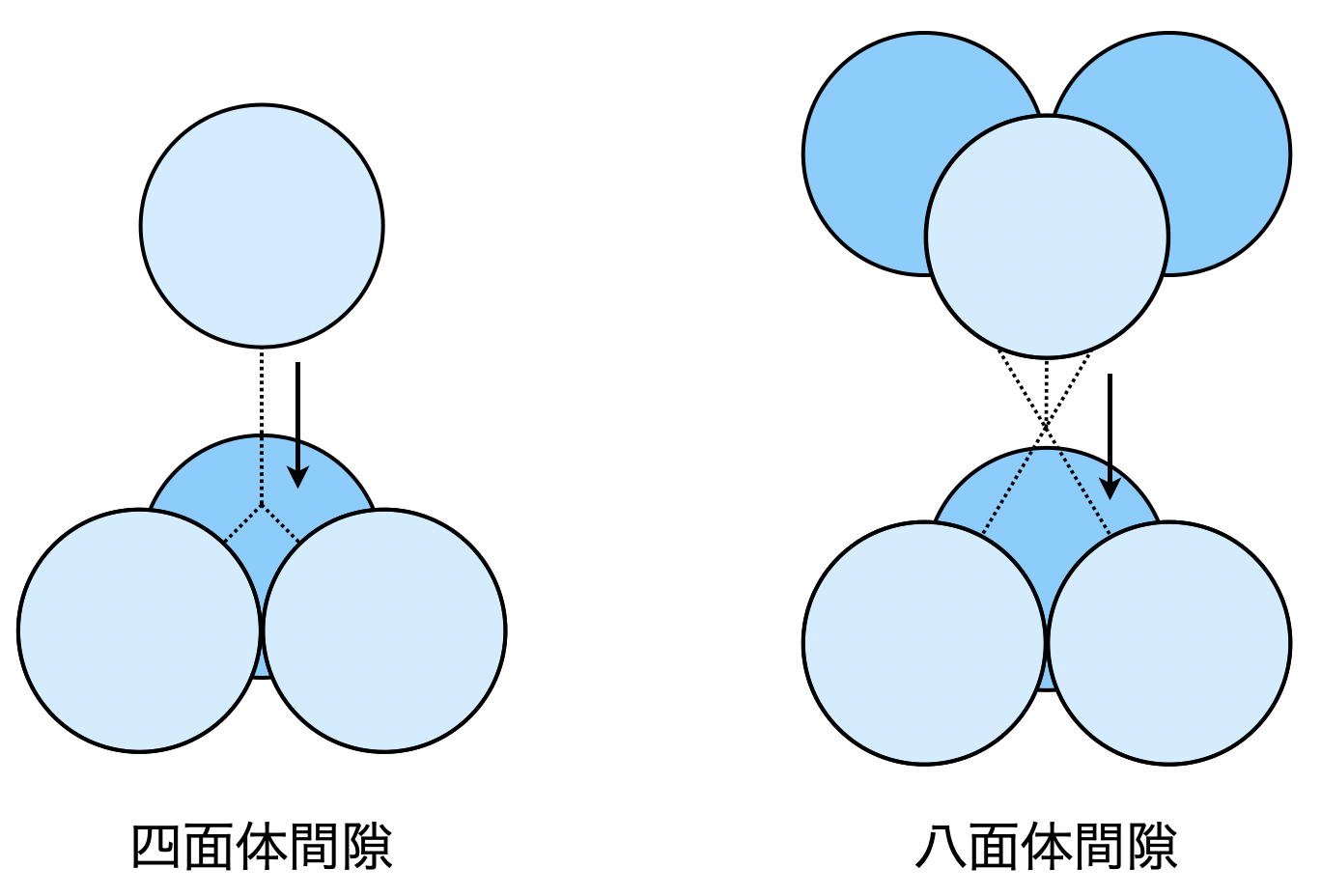
これを踏まえた上で,まず八面体間隙について考えていきます.八面体間隙は面心立方格子の各辺上に存在することがわかります.
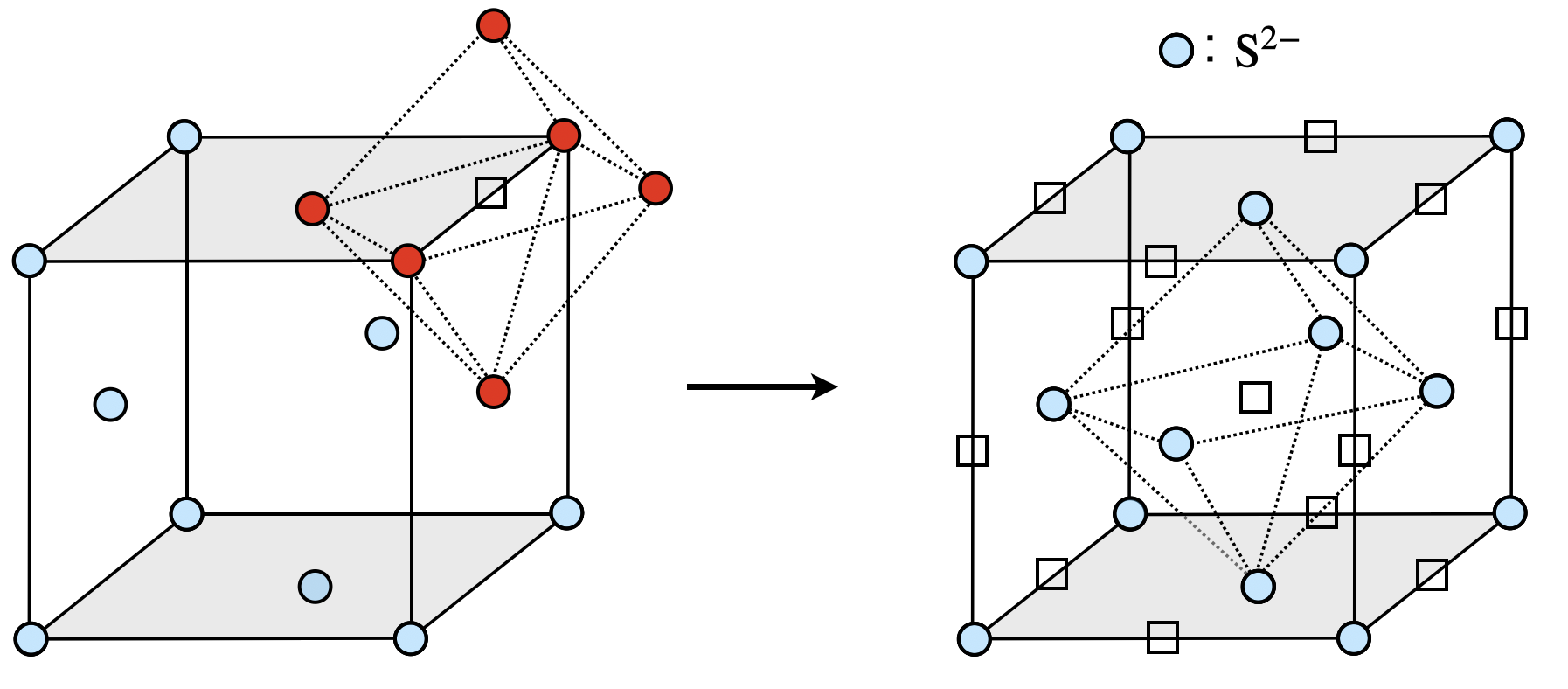
八面体間隙が単位格子中に含まれる個数は,
\(\large \frac{1}{4} \small × 4 × 3 + 1\ =\ 4個\)
次に,単位格子中に含まれ\(\rm{S^{2-}}\)の個数を調べてみましょう.
\(\large \frac{1}{2} \small × \large \frac{90^\circ}{360^\circ} \small × 8 + \large \frac{1}{2} \small × 6 = 4個\)
よって,\(1\)倍となります.
ここで,最密構造という言葉が出てきたので,結晶格子についても復習しておきましょう.
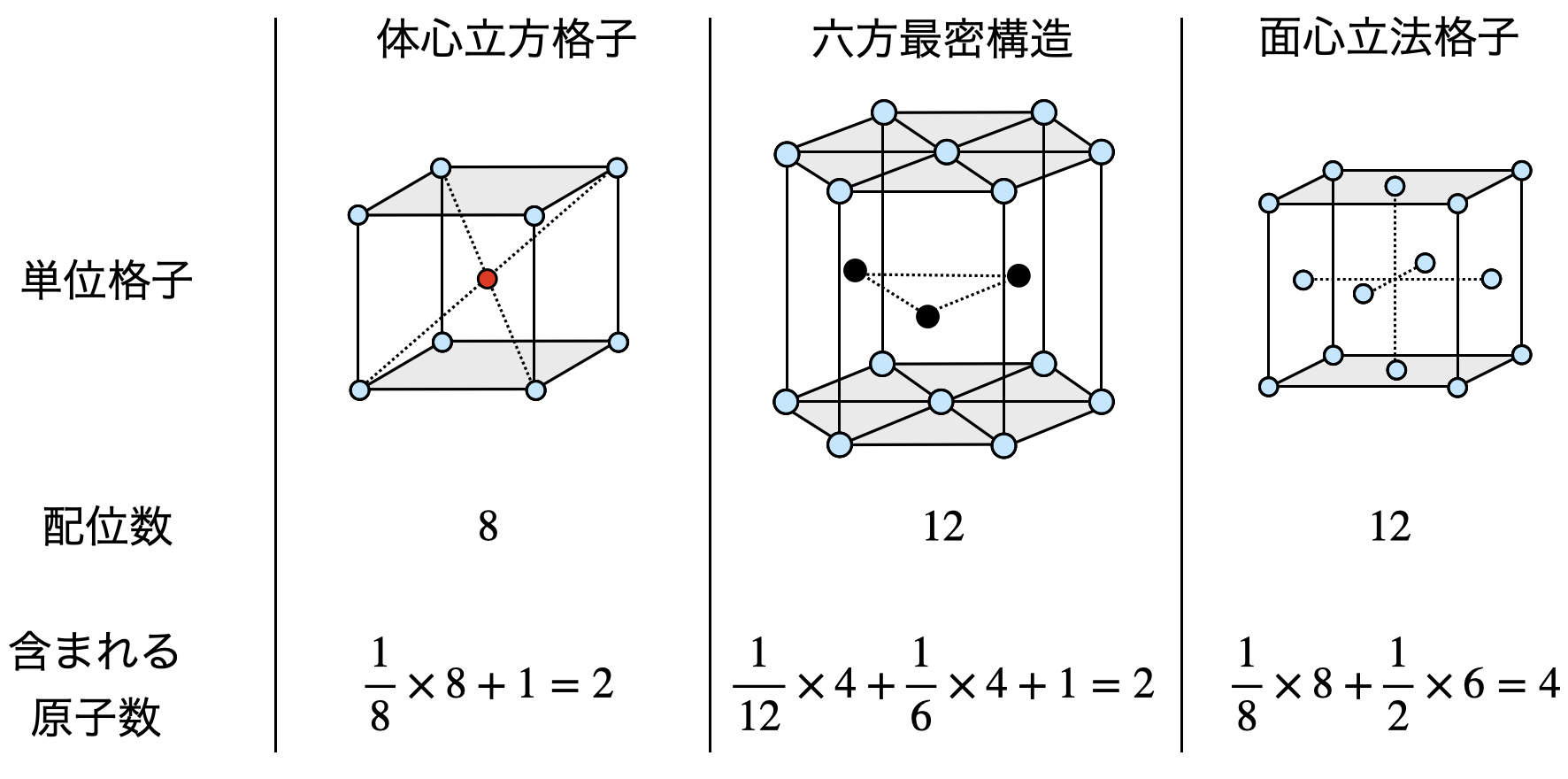
代表的な結晶格子には,体心立方格子,面心立方格子,六方最密構造があります.
この中で最密構造とは,同じ大きさの球を空間に最も密に積み重ねた構造のことをいいます.
ここで最密構造となる球の重ね方には,六方最密構造と立方最密構造(面心立方格子)があります.
①体心立方格子
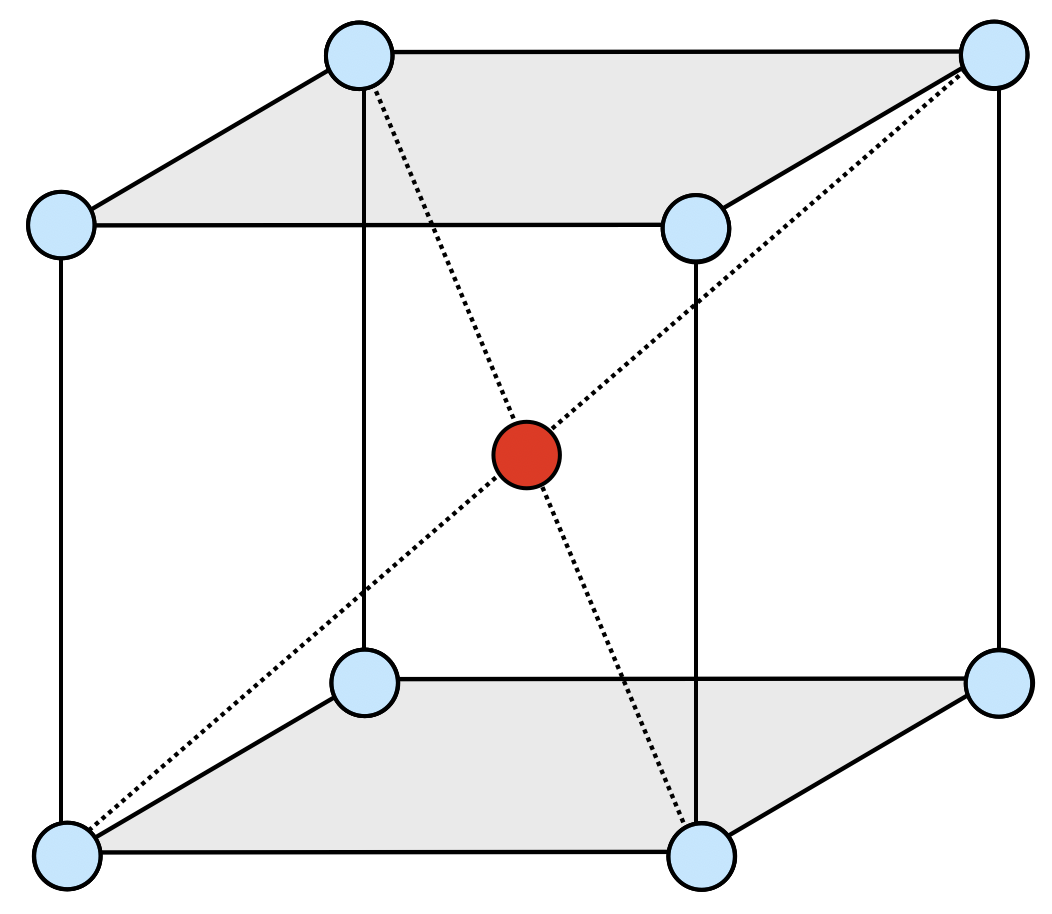
体心立方格子は,立方体の各頂点と立方体の中心に同種の粒子が配列された結晶格子です.
立方「体」の中「心」に原子があると考えると,覚えやすいと思います.立方体の中にある原子に着目すると,原子の配位数は\(8\)となります.
②六方最密構造
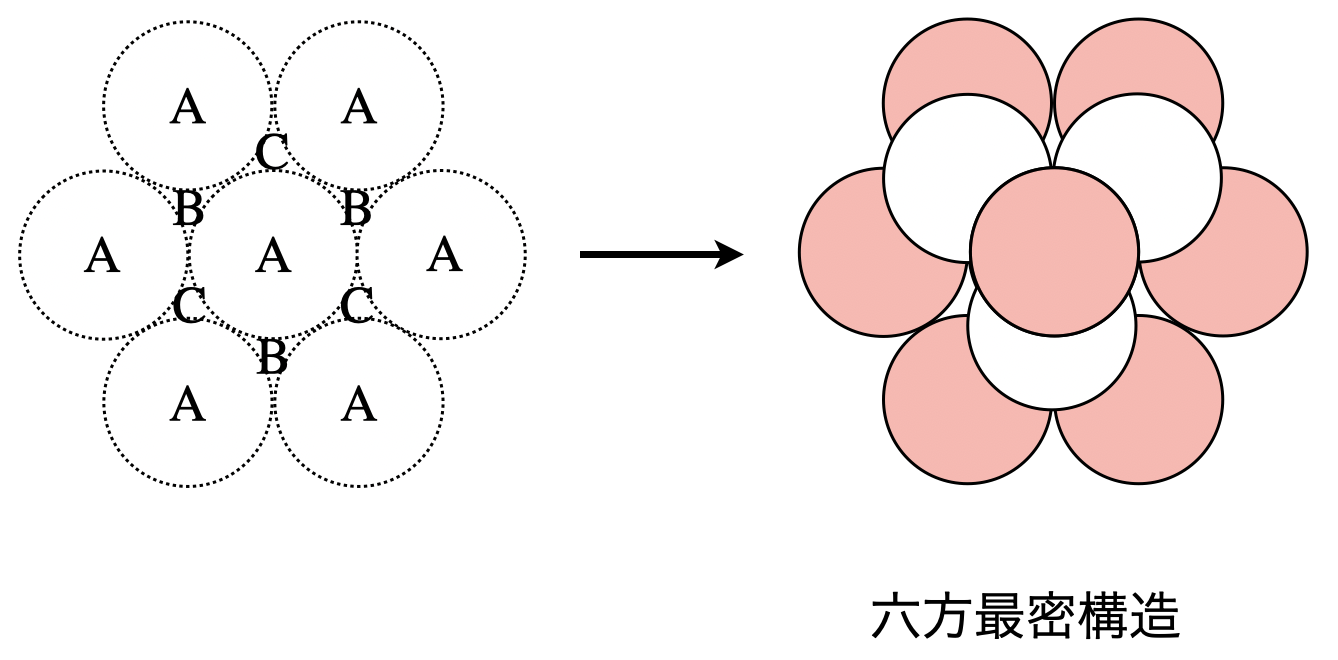
六方最密構造は,同じ大きさの球を最も密に積み重ねることで形成されます.
\(1\)層目は,下の図のようにそれぞれの球が\(6\)個の隣り合う球と接します.\(2\)層目は,\(1\)層目の\(3\)つの球のすき間にできる凹み\(\rm{B}\)の上に球を積み上げることで形成され,\(3\)層目として\(\rm{A}\)の真上に積み上げます.
そのため配列としては\(\rm{ABAB…}\)と\(2\)層周期となります.
ちなみに配位数が\(12\)であることも覚えておいてくださいね!
③面心立方格子
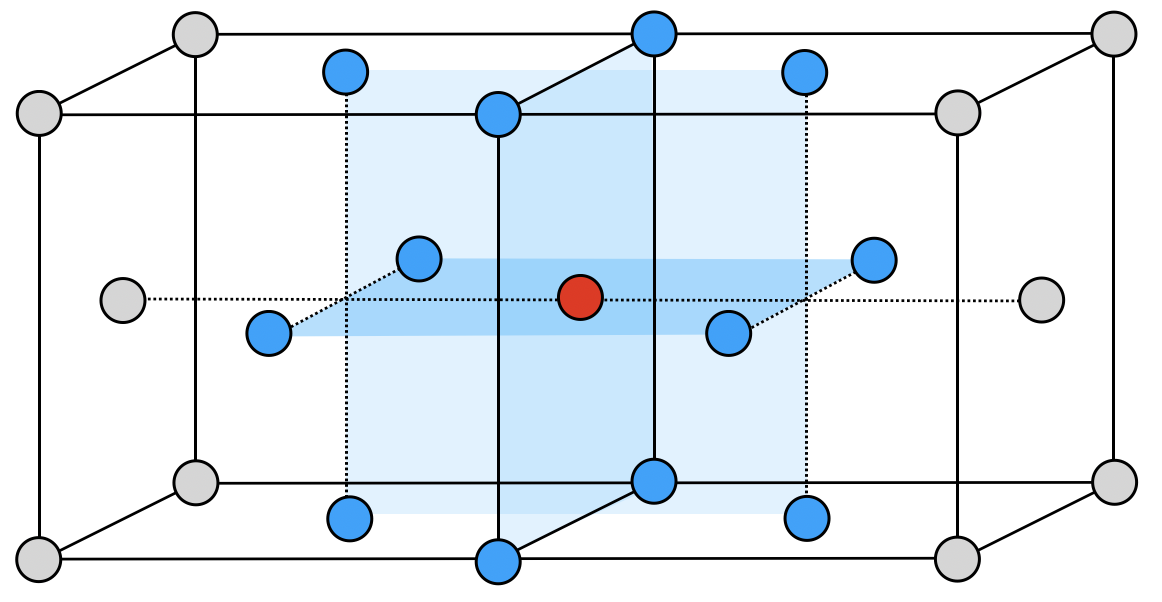
面心立方格子は,立方体の各頂点と各面の中心に同種の粒子が配列された結晶格子です.
各「面」の中「心」に原子があると考えると,これも覚えやすいです.
単位格子を横に\(2\)つ並べて赤丸の原子に着目すると,原子の配位数は\(12\)となります.
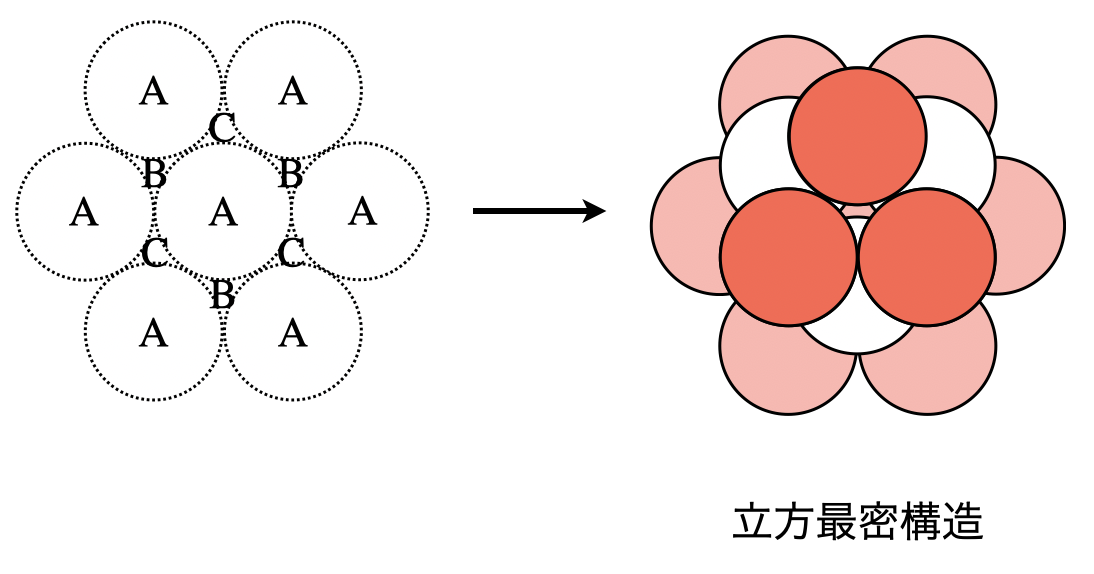
面心立方格子も最も密に積み重ねることで,形成されます.
\(1\)層目,\(2\)層目については六方最密構造と同じですが,\(3\)層目が違います.面心立方格子は\(3\)層目として\(1\)層目とは別の凹みである\(\rm{C}\)の上に球を積み上げます.これにより\(\rm{ABCABC…}\)と\(3\)層周期となります.
最後に,これらの単位格子の性質について簡単に表にまとめておきましょう.
い
次に,四面体間隙について考えていきましょう.
これについても面心立方格子で考えていきましょう.
四面体間隙は面心立方格子を\(8\)等分した小さい立方体の中心にあるので,単位格子中には\(8\)個含まれます.
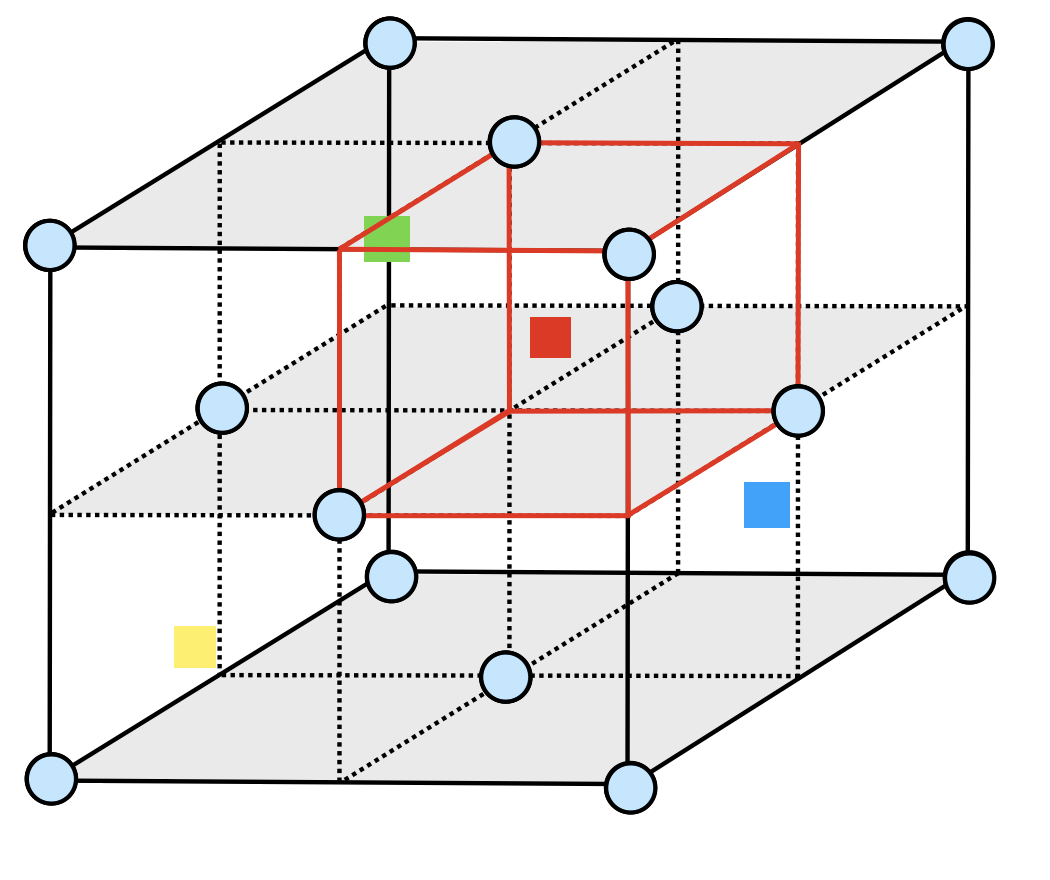
よって\(2\)倍であることがわかります.
う
この問題はウルツ鉱型構造についての知識がなくても,問題文の図\(3\)を見るだけで解答することができます.
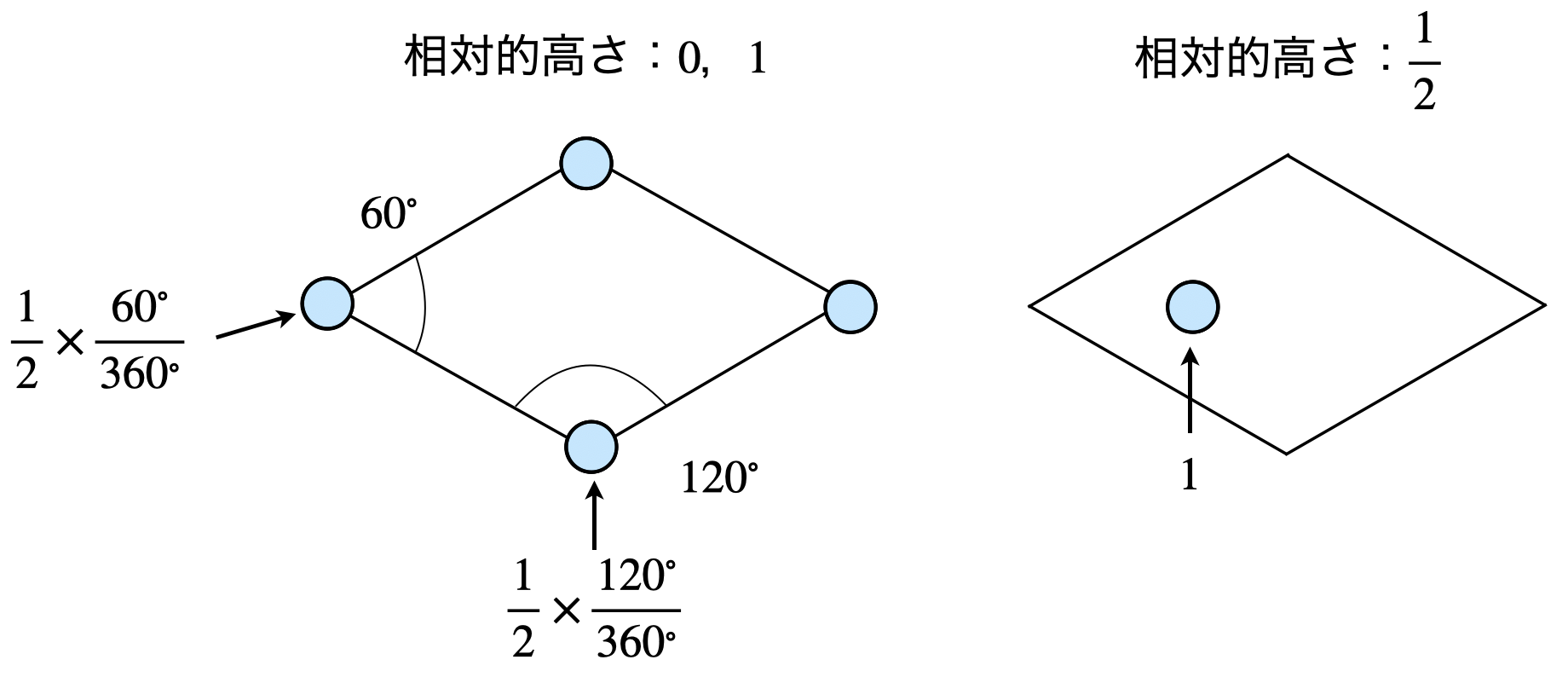
相対的高さ\(0,1\)のとき,
\(60^\circ\):まず上半分を除き\(\left( \large \frac{1}{2} \right) \),下半分について\(60^\circ\)分だけを考慮します.
\(120^\circ\):上半分を除き\(\left( \large \frac{1}{2} \right) \),下半分について\(120^\circ\)分だけを考慮します.
よって,
\(\large \frac{1}{12} \small × 2 + \large \frac{1}{6} \small × 2 = \large \frac{1}{2} \small 個\)
相対的高さ\(\large \frac{1}{2}\)のとき,
\(1\)個
よって,
\(\large \frac{1}{2} \small + 1 + \large \frac{1}{2} \small = 2個\)
問3
まず授業などではウルツ鉱型構造というのは学んでいないと思いますので,そこから解説していきましょう.
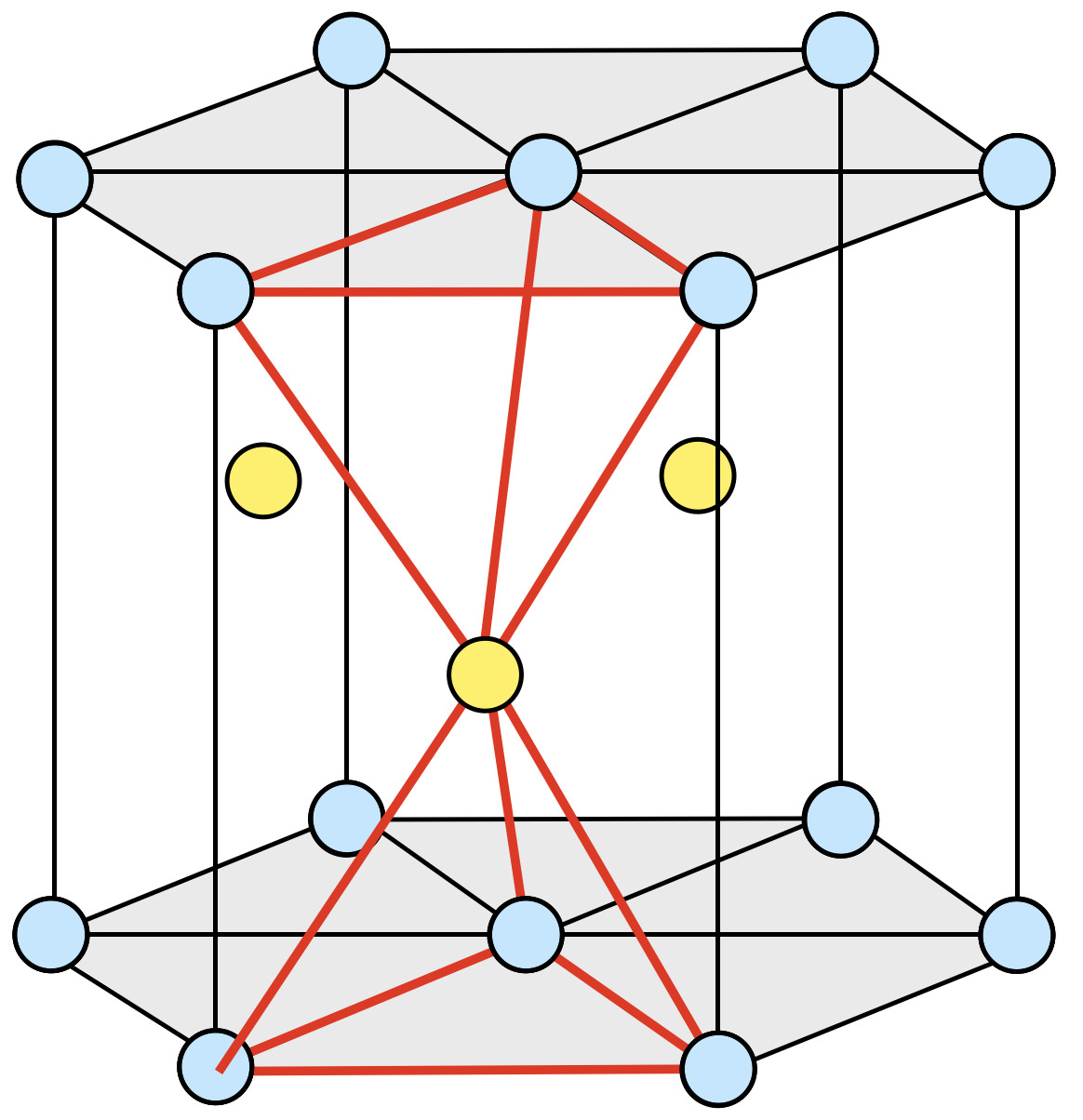
ウルツ鉱型構造は下のようになっています.
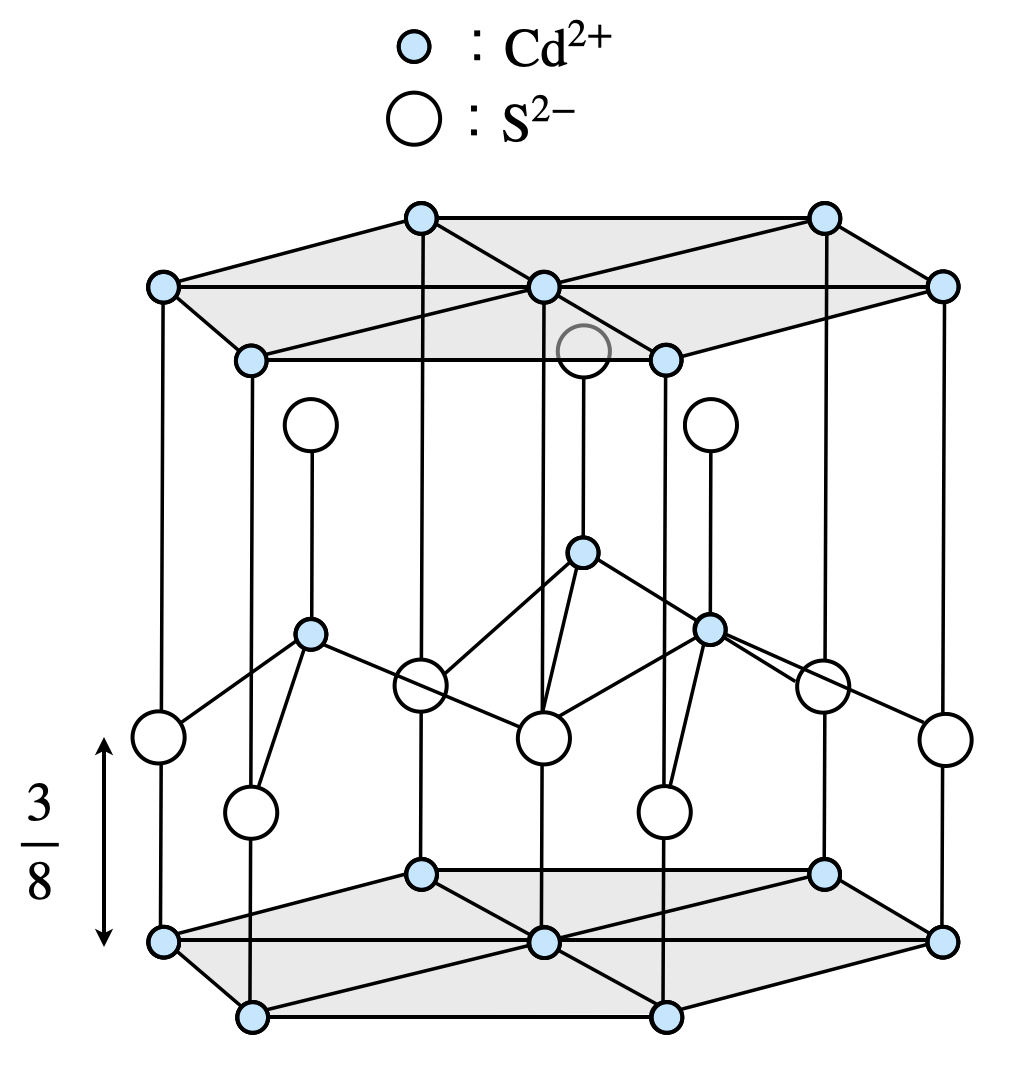
\(\rm{Cd}\)と\(\rm{S}\)がそれぞれ六方最密構造をとっていて,\(\rm{Cd}\)が作る六方最密構造の\(z\)方向に\(\large \frac{3}{8}\)ずれた位置に\(\rm{S}\)の六方最密構造が入っているという状態です.
このウルツ鉱型構造には正四面体が\(2\)個隠れています.そのため,正四面体の高さを\(2\)倍したものが\(h\)となります.
ここで,一辺を\(a\)とすると,正四面体の高さは\(\large \frac{\sqrt{6}}{3} \small a\)となります.(※下のポイントで解説しています.)そのため,
\(h = 2 × \large \frac{\sqrt{6}}{3} \small × 0.41 = 0.66 = 6.6 × 10^{-1}\ \rm{nm}\)
受験化学には,正四面体の高さが必要になるときがあります.
そのため正四面体の高さ = \(\large \frac{\sqrt{6}}{3} \small a\)となることは覚えておきましょう!ここで,その求め方を解説していきます.
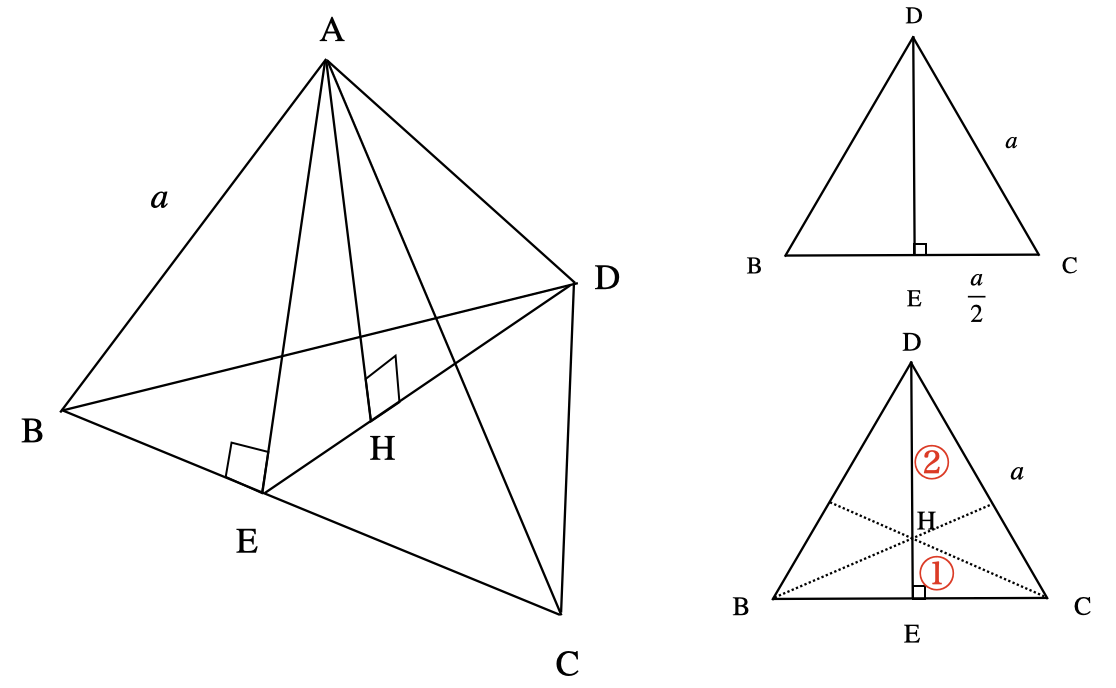
まず△\(\rm{DBC}\)について\(\rm{DE}\)を求めましょう.
このように立体の図形について考えるときは,平面図形に落とし込んで考えることが重要になります.
△\(\rm{DEC}\)について三平方の定理を用いると以下のようになります.
\(\rm{DE} = \)\(\sqrt{a^2 – \left(\large \frac{a}{2} \right)^2} \small = \large \frac{\sqrt{3}}{2} \small a\)
次に,△\(\rm{DBC}\)から\(\rm{EH}\)を求めます.ここで点\(\rm{H}\)は△\(\rm{DBC}\)の重心となっています.そのため\(\rm{DH:HE\ =\ 2:1}\)となります.
\(\rm{EH = \large \frac{1}{3} \small DE}\)\( = \large \frac{\sqrt{3}}{6} \small a\)
最後に△\(\rm{AEH}\)について三平方の定理を使用し,\(\rm{AH}\)を求めましょう.
\(\rm{AH = \sqrt{AE^2\ -\ EH^2} = \sqrt{DE^2\ -\ EH^2} = }\)\(\sqrt{\left( \large \frac{\sqrt{3}}{2} \small a \right)^2\ -\ \left( \large \frac{\sqrt{3}}{6} \small a \right)^2} = \large \frac{\sqrt{6}}{3} \small a\)
このような計算を入試中に行うのは大変なため,覚えて使いこなせるようにしましょう!
問4
この問題は非常に難易度が高く,制限時間内で完答するのは難しい問題です.そのため試験時には難問であると見抜き,飛ばしてもらってかまいません.むしろこの問題を飛ばし,他の問題に時間をかける方が合格するのに近道です.
一方で,このような難問の解き方を学ぶことで,今までに見たことないような問題にも対応できる力が身につきます.わかりやすく解説しますので,最後までついてきてください!
まず問題文の図\(4\)の閃亜鉛鉱型構造から考えていきましょう.
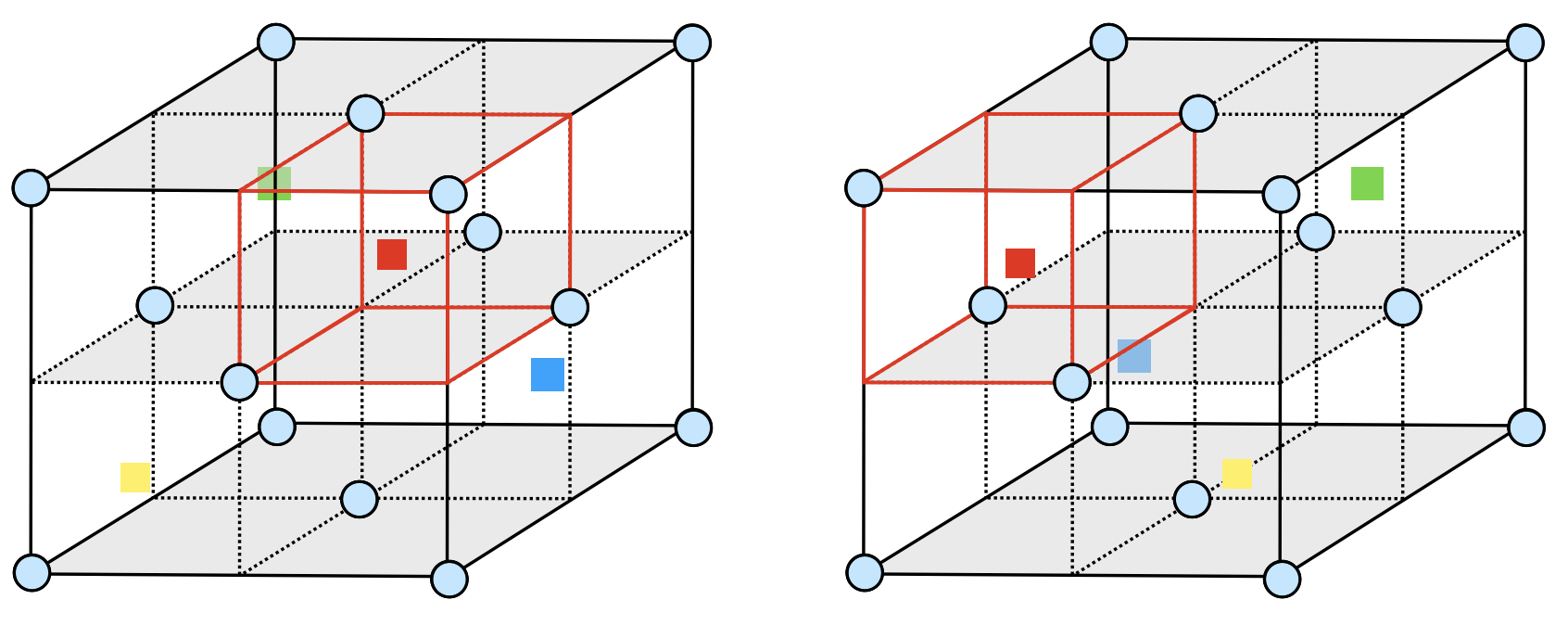
閃亜鉛鉱型構造とは下の図ような形をしており,立方体の\(\large \frac{1}{8}\)に正四面体が作られます.これが図に示すように,上段に\(2\)個,下段に\(2\)個配置されています.この配置方法が\(2\)通りあるという意味で,問題には\(2\)通りがあるという例が示されています.
次に,本問題で求められているウルツ鉱型構造について考えていきましょう.
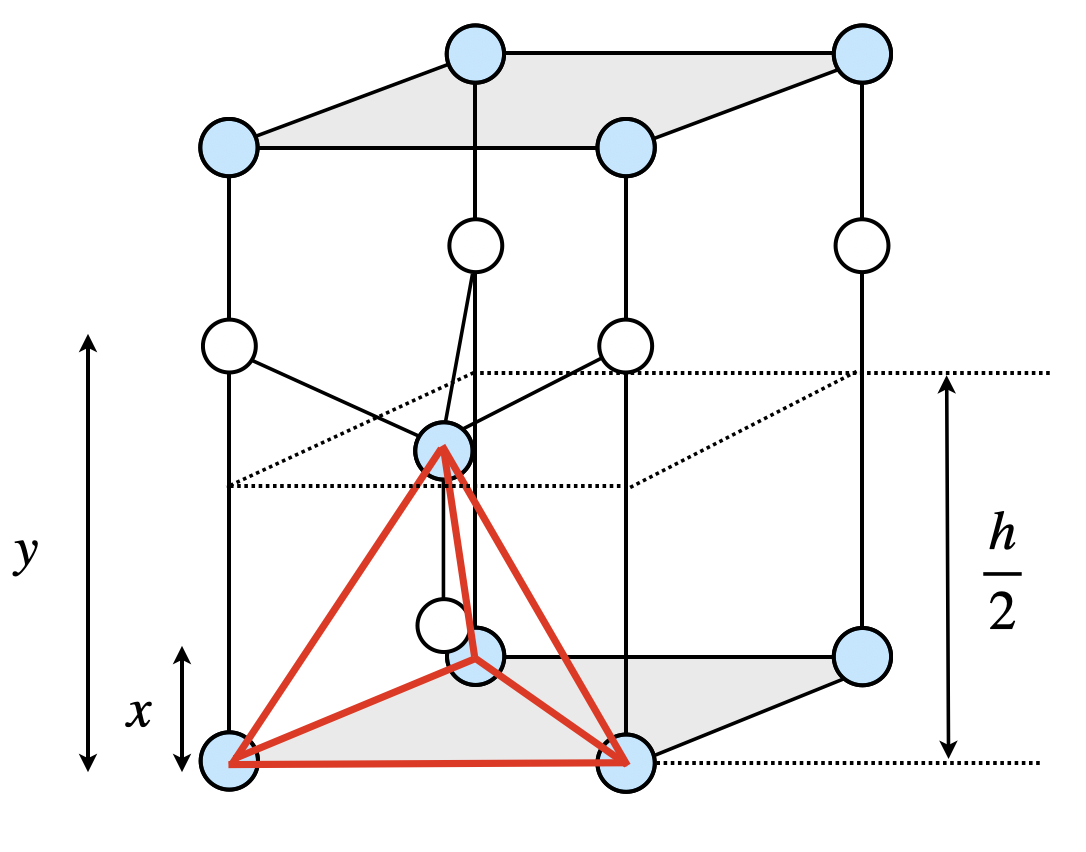
まず\(x\)を求めていきます.
赤線で囲まれた正四面体の重心に\(\rm{Cd^{2+}}\)は存在します.そのため\(\rm{Cd^{2+}}\)は正四面体の高さを\(3:1\)に内分する点となります.
\(\large \frac{h}{2} \small:x = 4:1\)
\(x = \large \frac{h}{8}\)
次に,\(y\)を求めていきます.
\(y\)を求めるときには,\(\rm{Cd^{2+}}\)を頂点とする正四面体を考えます.この正四面体も先ほどと同じように高さは\(\large \frac{h}{2}\)となるので,下面から考えると,
\(y = x + \large \frac{h}{2} \small = \large \frac{5}{8} \small h\)
となります.
よって,お,きの断面図は以下のようになります.
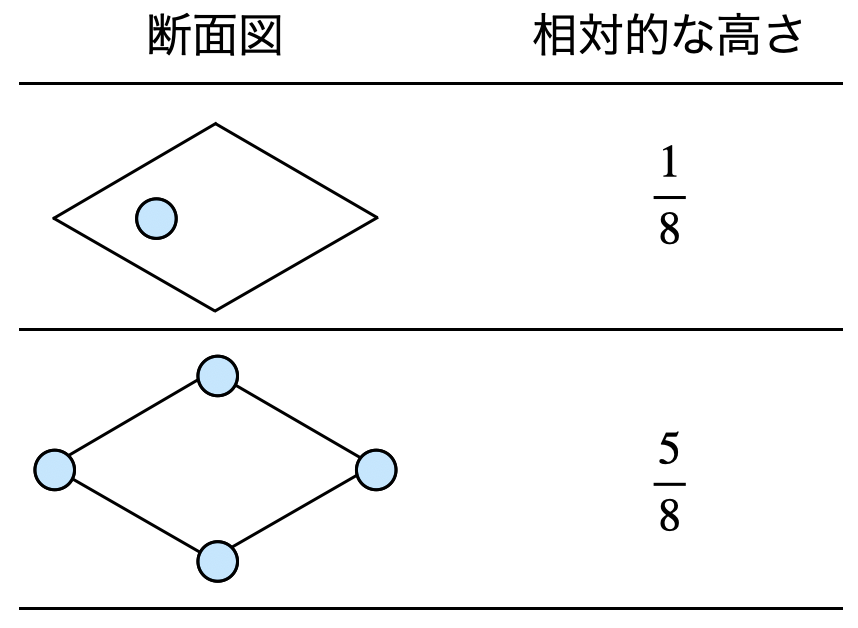
け,さについてはお,きで考えたものを上下逆にしたものと考えることができます.そのため,以下のような解答になります.
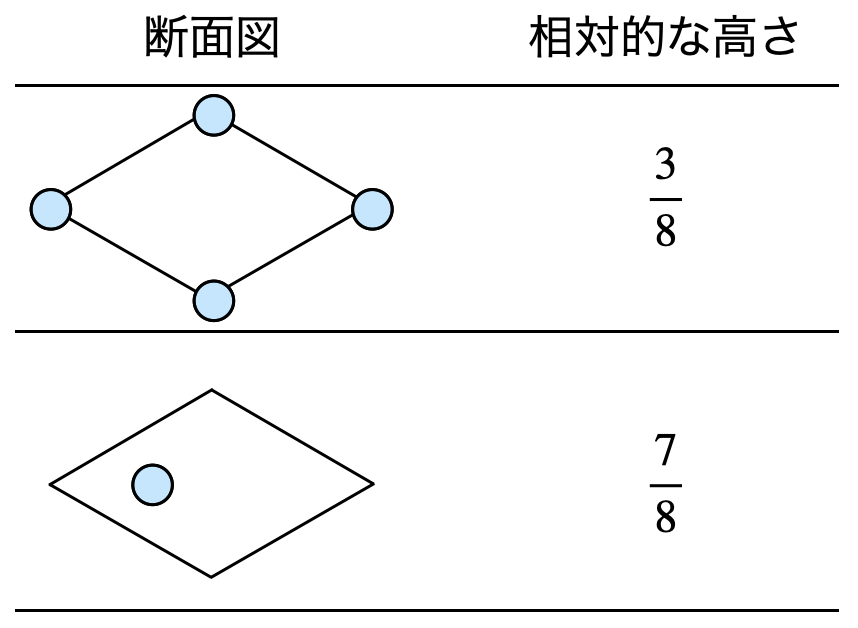
最後に
大問\(1\)の解説だけで非常に長くなってしまいました.最後まで閲覧していただきありがとうございました.
本記事の内容についてわからない点があれば,遠慮なく質問していただければと思います.
(Twitter:chem_story1)
京都大学の化学は難問が多いと言われますが,その分多くのことを学ぶことができます.
京都大学志望でない方でも本記事を読んでいただいて,皆さんの学習の一助になれば幸いです.
大問2についてはこちらの記事をご覧ください!




コメント