
大問2の総評
初めまして,こんにちは.KUTです.
本記事では,徹底解説シリーズとして2020年京大化学の大問2について解説していきます.また解説に加えて,それぞれの問題で覚えておいてほしいポイントについて詳しく説明していきます.
京大の化学は難しいという印象が強い方が多いと思いますが,京大化学には難しい問題と標準問題の2つがあります.ここで,受験生が対策すべきことが2つあります.
1つ目は,標準問題を最後まで解き切る力を身につけることです.これにより,まずは平均点を取ることを目指します.
2つ目は,難しい問題と標準問題を見分けられる目を養うことです.試験本番は時間制限内に自分の解ける問題を解き切る必要があります.そのため,難しい問題は解かずに,標準問題をしっかりと選択していきながら,最後まで解いていくことが必要になります.
この記事では,問題を選択していく目を養うために,どのようにして判断していくのかということも自分なりに説明していきます.
京都大学の化学は基本的に穴埋め問題が中心です.この穴埋め問題をクリアできるかどうかが鍵となります.穴埋め問題ということは,前後の文章により誘導があるということです.この誘導を味方にできるかが重要になります.
2020年大問2については,
(a):沸点上昇・蒸気圧降下・電気分解
蒸気圧や電気分解などが絡む問題で少し難しいです.
基礎をしっかりと理解して使いこなせるようにしておく必要があります.
(b):気相平衡
不均一系の気相平衡についての問題でした.
それでは,2020年京大化学の大問2の解説に進んでいきましょう!
大問2(a)
大問\(2(\rm{a})\)は蒸気圧降下や電気分解に関する問題です.
それぞれの問題を解いていきながら,押さえてほしいポイントを徹底的に解説していきます.
問1
容器内の水に\(\rm{NaCl}\)や\(\rm{CaCl_2}\)が溶解することで,沸点上昇が生じています.
ここで沸点上昇について復習しておきましょう!
溶液では溶媒粒子と溶質粒子が均一に混じり合って自由に位置を変えています.この点では,溶液として特別な性質があるわけではありません.
性質が現れるのは,溶媒粒子と溶質粒子が別々の行動を行うときです.このとき,蒸気圧降下,沸点上昇,凝固点降下,浸透圧という\(4\)つの性質が現れます.この中で今回は蒸気圧降下と沸点上昇について説明していきます.
①蒸気圧降下
一般として,溶媒である水分子(\(\rm{H_2O}\))と溶質\(\rm{B}\)を考えてみましょう.
ここで溶媒である\(\rm{H_2O}\)は蒸発するとし,溶質\(\rm{B}\)は液の表面から蒸発しないとします.(蒸発しないという性質のことを不揮発性といいます!)すると,溶媒粒子と溶質粒子は別々の行動を取ることになりますね.その結果溶液全体で見ると,液の表面から溶媒である\(\rm{H_2O}\)が蒸発しようとすると,溶質\(\rm{B}\)が邪魔をするため,溶質\(\rm{B}\)を加えた分だけ蒸気圧が下がることになるのです.このような蒸気圧が下がる現象を蒸気圧降下といいます.

②沸点上昇
先程の容器を加熱し,温度を上げることを考えます.温度を上昇させると,液面のすぐ近くの蒸気の圧力は,その温度で決まる飽和蒸気圧まで増加しており,やがて大気圧と等しくなります.その後,沸騰が起こります.
ここで,沸騰を理解するにも注意が必要です.沸騰とは,「液体の表面だけでなく,液体内部からも蒸気(気泡)が発生する」現象のことをいいます.
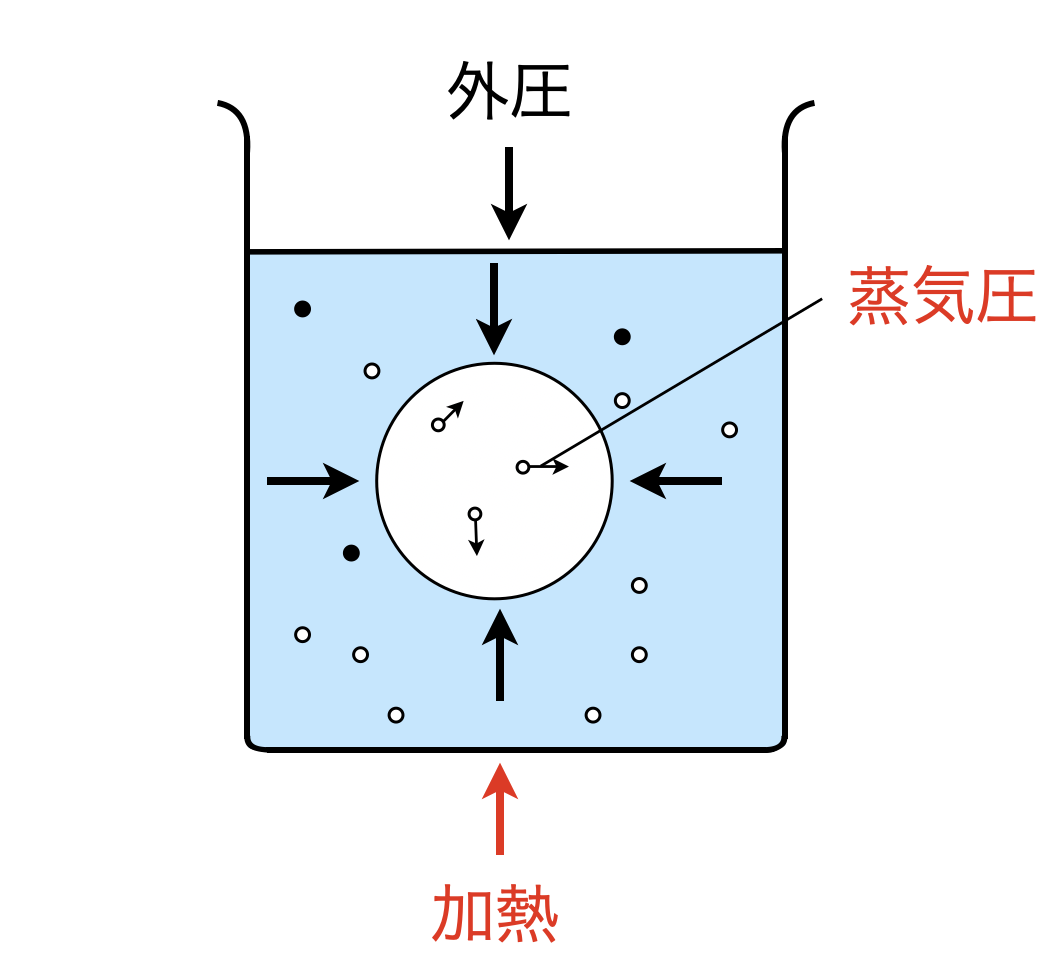
この沸騰時の気泡は水分子のみでできていて,そこにでは溶質\(\rm{B}\)は存在しません.すなわち,沸騰という現象時にも溶媒分子と溶質分子は別々に行動します.
先程の\(①\)から純溶媒と比較して溶液では蒸気圧が減少しています.そのためより温度を上げないと蒸気圧を大気圧と等しくすることはできないため,沸点が上昇します.この現象を沸点上昇といいます.沸点上昇\(\Delta T_{\rm{b}}\)(\(\rm{b:boiling\ point}\))を求めるためには,以下の式を用います.
\(\Delta T_{\rm{b}}\ =\ K_{\rm{b}}\ m\)

ここで,\(K_{\rm{b}}\)はモル沸点上昇と呼ばれる比例定数です.\(m\)は質量モル濃度で,単位に注意が必要です.単位は\(\rm{mol/kg}\)(溶媒)です.なぜこの式を用いるのかは大学の熱力学を勉強する必要があるため,今回は覚えてください!もしリクエストが多ければ,記事にしますね!
それでは次に,これらの事象を状態図で理解していきましょう.
問題を解くためには,原理を理解することも大切ですが,状態図などの図解ですぐに知識を呼び戻せることが非常に大切です.
蒸気圧降下は気液平衡時の圧力,沸点上昇は気液平衡時の温度についてです.では溶質を加えると蒸気圧曲線はどのようになるのでしょうか?
液相から気相へ出ていく溶媒分子が減少しますが,気相から液相へ戻ってくる溶媒分子は変化しません.そのため気液平衡が成り立っていないことになります.この気液平衡を成立させるために,気相から液相へ入る溶媒分子が多くなり,最終的には気相が消えてしまいます.この現象を状態図で考えると,液相の領域が広がり,純溶媒の気液境界線が溶液中の溶媒の液相領域に含まれることとなります.
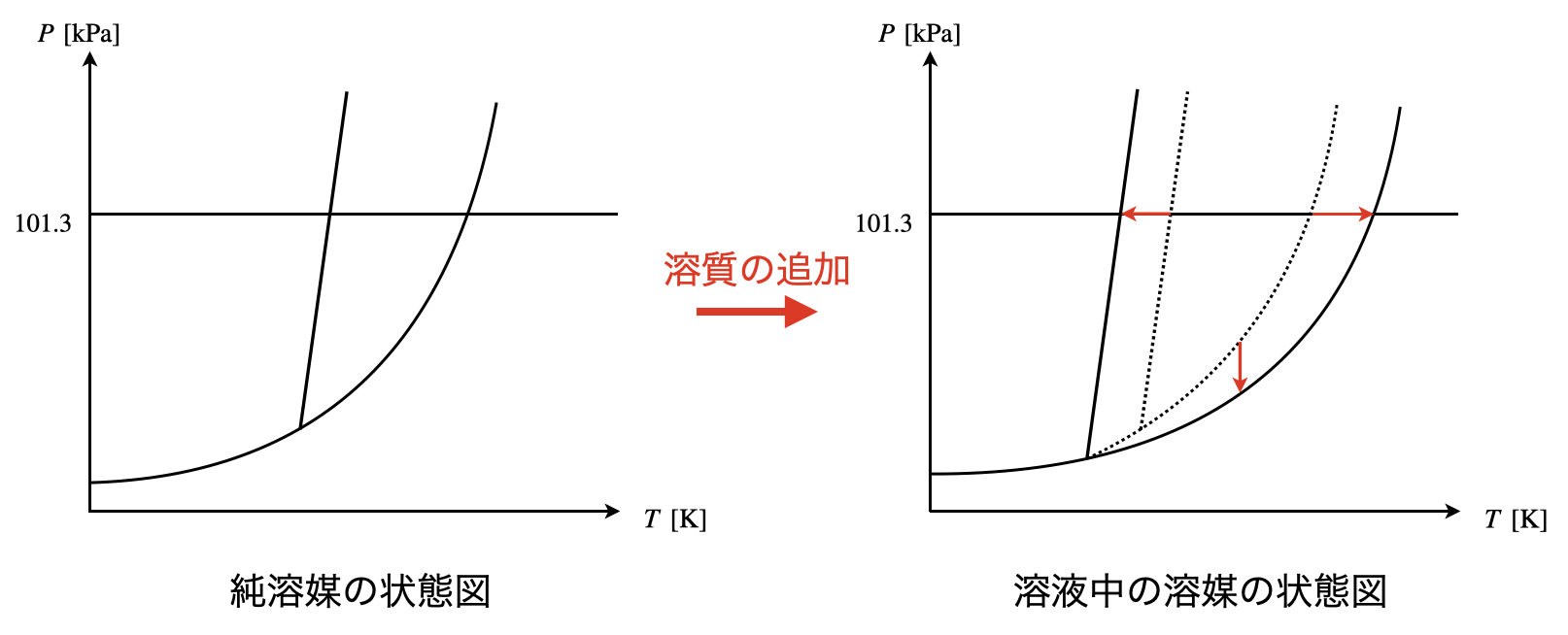
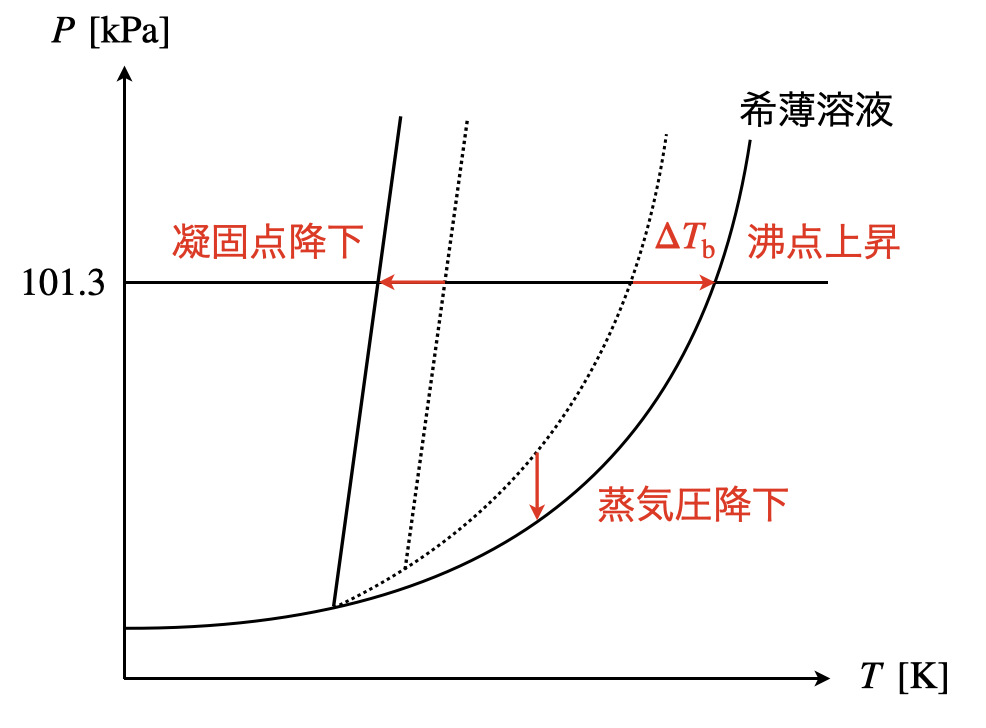
この図を見ると,沸点上昇や蒸気圧降下だけでなく,凝固点降下についても覚えやすくなります.
ぜひ,この機会に覚えてくださいね!
前置きがだいぶ長くなってしまいましたが,それでは問題を解いていきましょう!
問題に与えられた図より,沸点上昇\(\Delta T_{\rm{b}}=2^\circ \rm{C}\)であることがわかります.
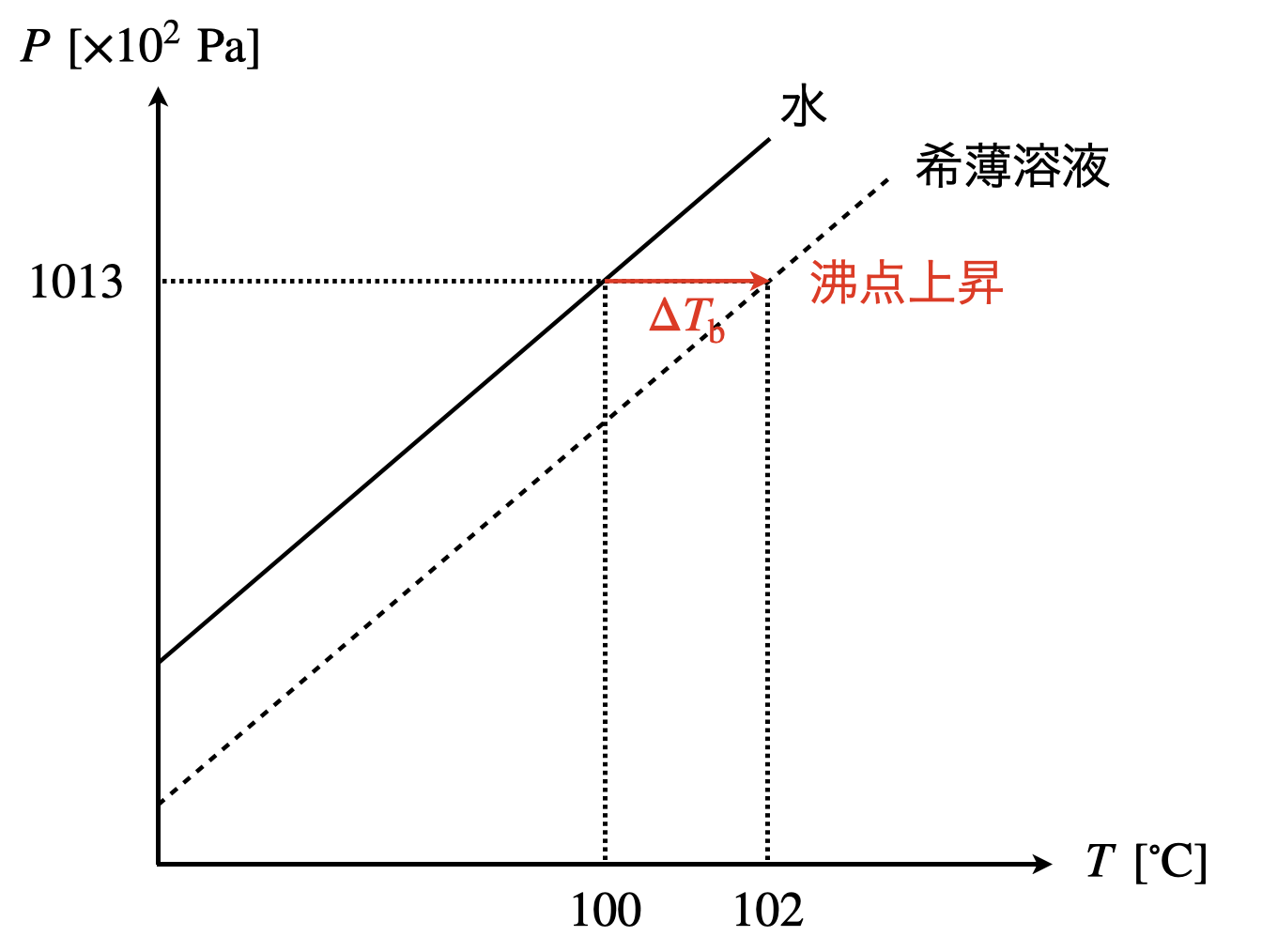
また溶液に加えた\(\rm{CaCl_2}\)を\(x\ \rm{mol}\)とすると,\(\rm{NaCl}\)と\(\rm{CaCl_2}\)は物質量比が\(1:1\)であるため,\(\rm{NaCl}\)も\(x\ \rm{mol}\)となります.それぞれは以下のように電離します.

すると溶液全体では,総イオンの物質量は\(5x\ \rm{mol}\)となります.以上より,質量モル濃度\(m\)は以下のようになります.
\(m = \large \frac{5x}{(1.3\ ×\ 10^2 )\ ×\ 10^{-3}}\ \small \rm{mol/kg}\)
これを沸点上昇の式:\(\Delta T_{\rm{b}}\ =\ K_{\rm{b}}\ m\)に代入すると,\(x\)を求めることができます.
\(2 = \large \frac{5.2\ ×\ 10^{-1}\ ×\ 5x}{(1.3\ ×\ 10^2)\ ×\ 10^{-3}}\)
\(x = 0.1\ \rm{mol}\)
問2
操作\(\rm{\,I\,}\)では装置内の圧力を大気圧にした後,バルブを閉じているため,操作\(\rm{\,I\,}\)終了時には気相には「空気」と「水蒸気」が存在します.それぞれの圧力について考える必要があるので注意していきましょう!
操作\(\rm{\,I\,}\)での空気の分圧を\(p_{\rm{Air, \,I\,}}\),水蒸気の分圧を\(p_{\rm{H_2O, \,I\,}}\),操作\(\rm{I\hspace{-.01em}I}\)での空気の分圧を\(p_{\rm{Air, I\hspace{-.01em}I}}\),水蒸気の分圧を\(p_{\rm{H_2O,I\hspace{-.01em}I}}\)として,それぞれを求めていきましょう!
まずは操作\(\rm{\,I\,}\)です.操作\(\rm{\,I\,}\)でガラス容器を割る前は,溶液は水のみであるため,\(T=87^\circ \rm{C}\)で,\(p_{\rm{H_2O, \,I\,}} = 624\ ×\ 10^2\ \rm{Pa}\)であることがわかります.そのため,
\(p_{\rm{Air, \,I\,}} = (1013\ -\ 624)\ ×\ 10^2 = 389\ ×\ 10^2\ \rm{Pa}\)
となります.
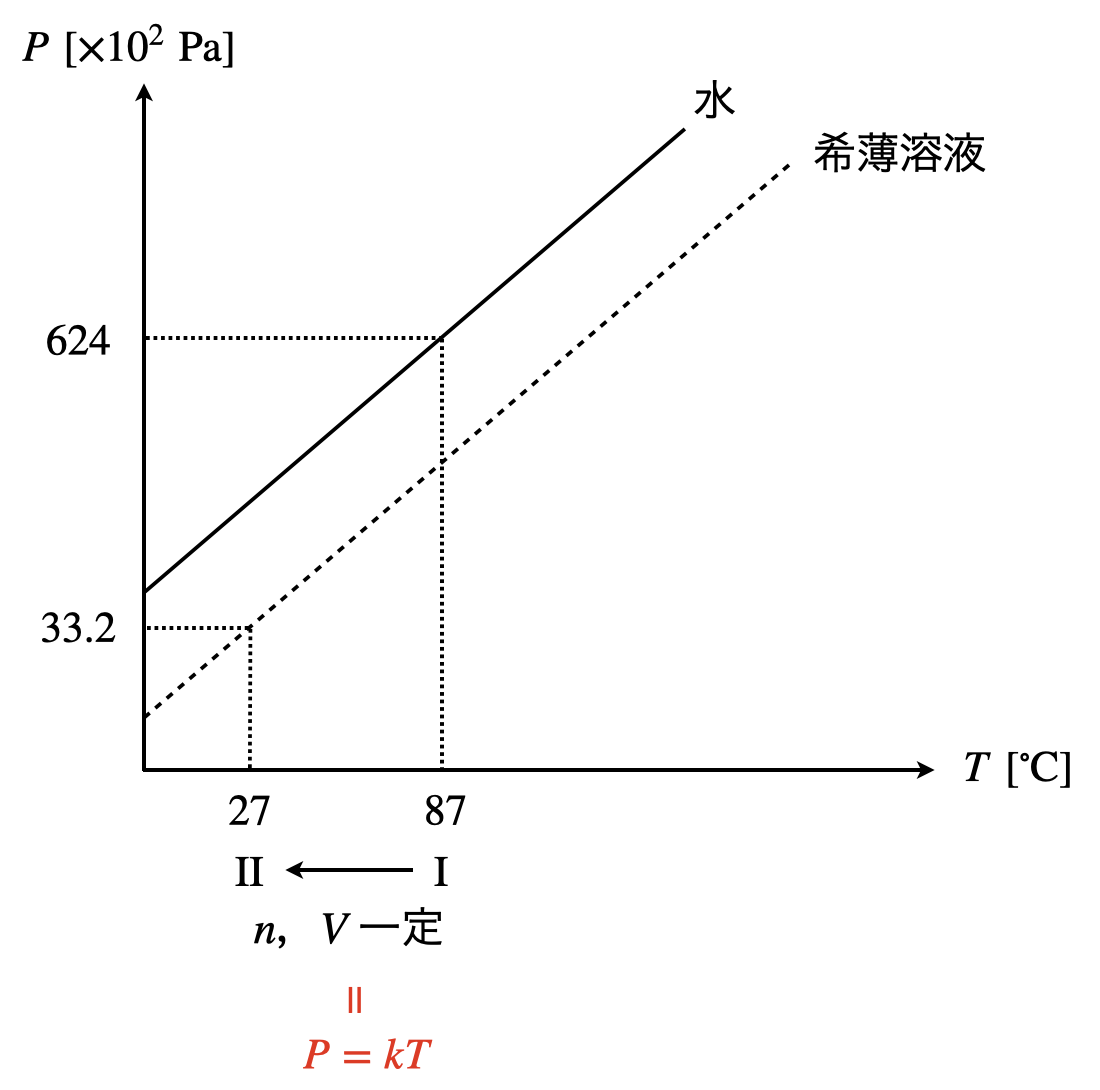
次に,操作\(\rm{I\hspace{-.01em}I}\)として温度を下げ,\(T=27^\circ \rm{C}\)とすると,グラフより希薄溶液の蒸気圧は\(p_{\rm{H_2O,I\hspace{-.01em}I}} = 33.2\ ×\ 10^2\ \rm{Pa}\)となります.\(p_{\rm{Air, I\hspace{-.01em}I}}\)は,\(pV=nRT\)より\(V,n\)を一定とすると,\(p=kT\)となります.よって,
\(\large \frac{p_{\rm{Air, I\hspace{-.01em}I}}}{T_{\rm{I\hspace{-.01em}I}}} \small = \large \frac{p_{\rm{Air, \,I\,}}}{T_{\rm{\,I\,}}}\)
\(p_{\rm{Air, I\hspace{-.01em}I}} = \large \frac{T_{\rm{I\hspace{-.01em}I}}}{T_{\rm{\,I\,}}} \small p_{\rm{Air, \,I\,}} = \large \frac{273\ +\ 27}{273\ +\ 87}\ \small ×\ 389\ ×\ 10^2 = 324\ ×\ 10^2\ \rm{Pa}\)
したがって,
\(全圧 = p_{\rm{H_2O,I\hspace{-.01em}I}} + p_{\rm{Air, I\hspace{-.01em}I}} = (33.2\ +\ 324)\ ×\ 10^2\ \rm{Pa} = 357\ ×\ 10^2\ \rm{Pa} = 3.57\ ×\ 10^4\ \rm{Pa}\)
この問題では,操作\(\rm{\,I\,}\)の最初では\(\rm{Cl^-}\)が含まれていないので,水の蒸気圧曲線を読み取る必要がありますが,ガラス容器を割った後は\(\rm{Cl^-}\)が含まれるので,希薄溶液の蒸気圧曲線を読み取る必要があります.
この点に注意して演習していってください!!
問3
操作\(\rm{I\hspace{-.15em}I\hspace{-.15em}I}\)において,電流を流したときの各白金電極の反応を考えていきましょう!
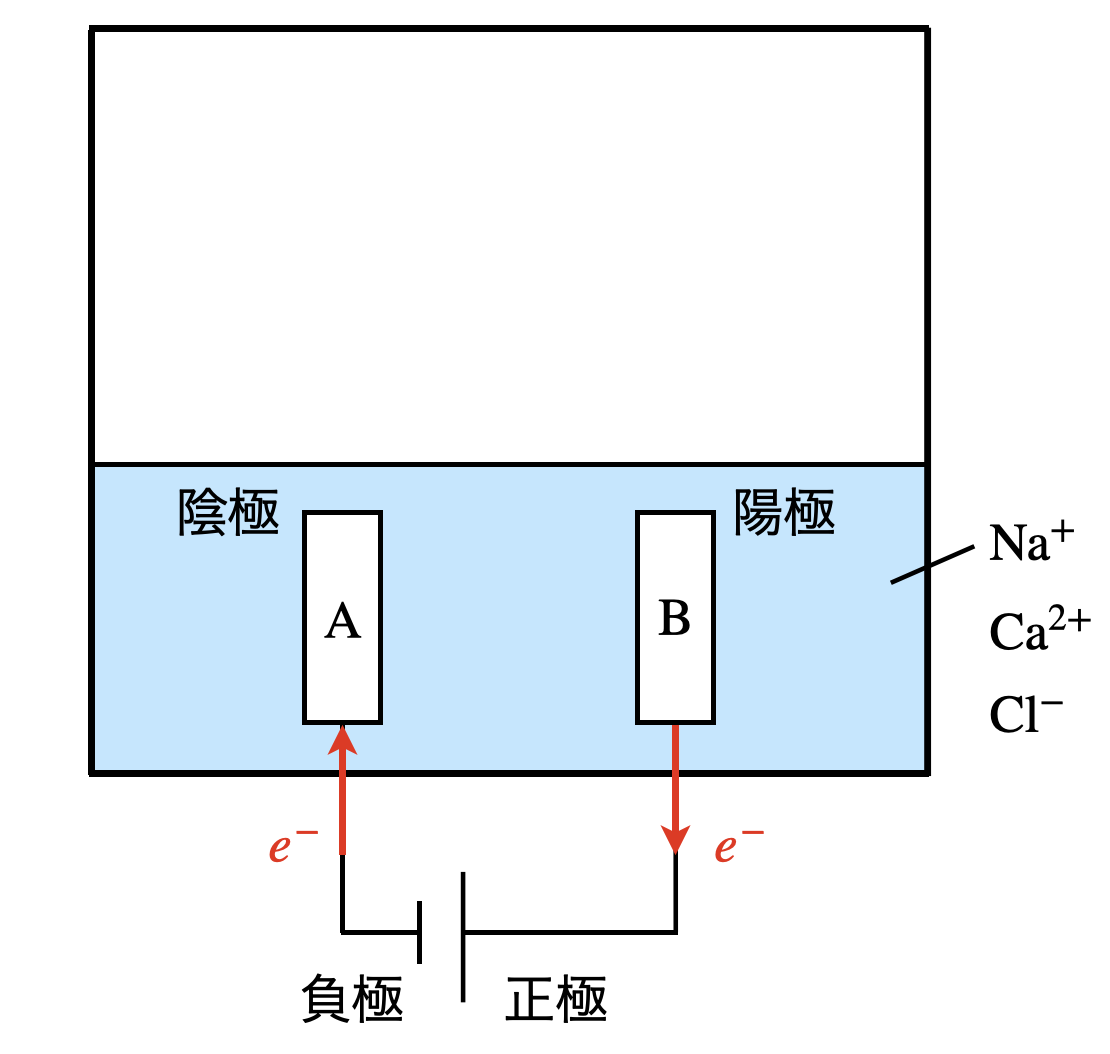
\(\rm{NaCl,CaCl_2}\)はそれぞれ完全に電離するため,溶液中には\(\rm{Na^+,Ca^{2+},Cl^-}\)が存在します.このような電気分解の問題では,\(e^-\)の流れを図に描き込むことが大切です!必ず書いてくださいね!!
電極\(\rm{A}\)は陰極となり,\(e^-\)を得ます.溶液中に溶けているイオンを物質を見ると,\(\rm{Na^+,Ca^{2+},H_2O}\)が存在します.その中で,\(\rm{Na^+,Ca^{2+}}\)はイオン化傾向が高いため,反応しません.そのため,\(\rm{H_2O}\)が以下のように\(e^-\)を得て,反応します.
\(\rm{A:H_2O\ +\ }\)\(2e^-\ →\ \rm{H_2\ +\ 2OH^-}\)
電極\(\rm{B}\)は陽極となり,\(e^-\)を放出します.溶液中に溶けているイオンを物質を見ると,\(\rm{Cl^-}\)が存在します.
\(\rm{B:2Cl^-\ →\ Cl_2\ +\ }\)\(2e^-\)
最後に,電気分解の復習をしておきましょう!
電気分解の問題を解く上で重要なことが\(3\)点あります!
①陰極・陽極の決定
②電解槽の回路図を描き,電子の流れを書く
③陰極・陽極における反応の序列,反応式を覚える
この\(3\)点に注意すれば,必ず解くことができます!
①陰極・陽極の決定
電源の\(+\)極が正極となり,そこにつながる電極が陽極となります.つまり,電源の\(+\)極につながっているところはすべて\(+\)になります.
電源の\(-\)極が負極となり,そこにつながる電極が陰極となります.つまり,電源の\(-\)極につながっているところはすべて\(-\)になります.
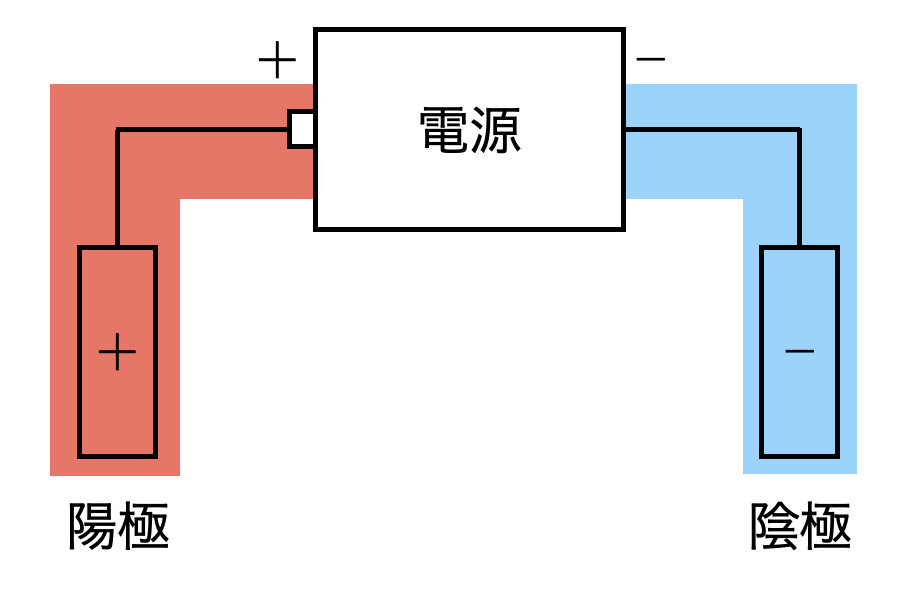
②電解槽の回路図を描き,電子の流れを書く
下の図のように必ず,電子の流れを書くようにしてください!\(e-\)は陽極から出て,陰極に入ると覚えてください!
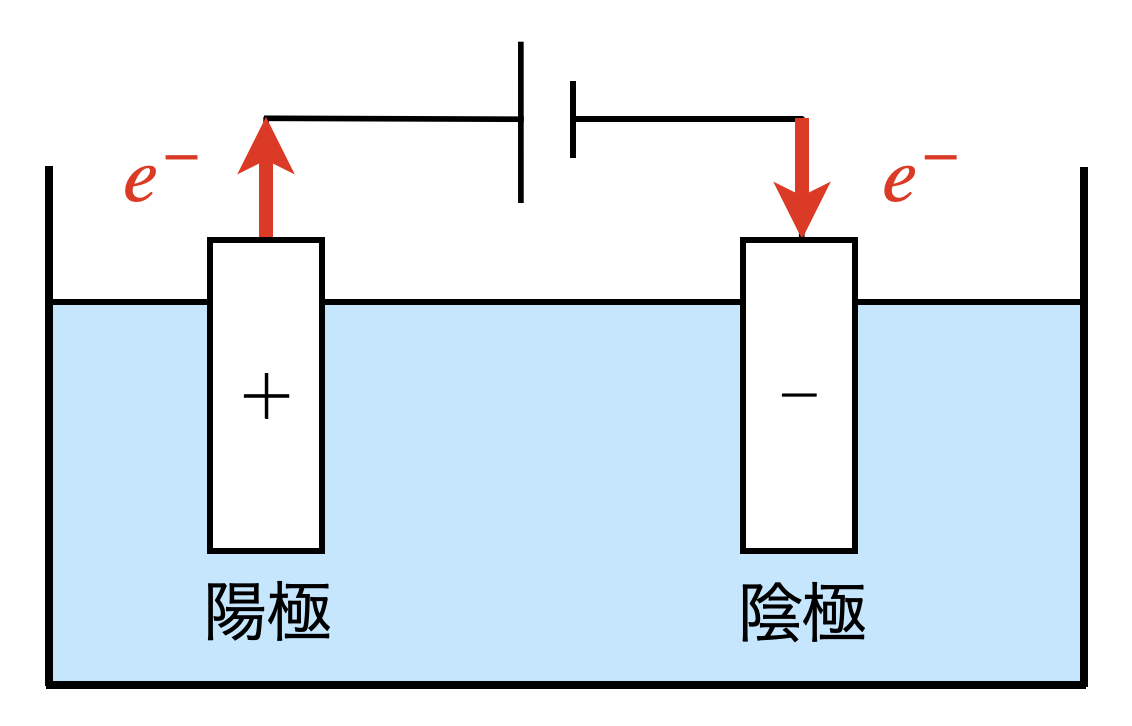
③反応の序列を覚える
反応の序列を覚えるために,まずイオン化傾向を覚えてましょう!
イオン化傾向とは,金属が水または水溶液中で電子を放出し,陽イオンになろうとする性質のことです.簡単にいうと,陽イオンのなりやすさです.イオン化傾向が高い金属は,陽イオンになりやすい,つまり単体よりも陽イオンでいたいということです.そのためこの問題では,\(\rm{Na^+,Ca^{2+}}\)はイオン化傾向が高い,つまり単体よりも陽イオンでいたいため,反応しないということです.

これをまず覚えてくださいね!
その中で,陰極での反応をコンパクトにまとめると,\(\rm{Ag^+ > Cu^{2+} > H^+}\)の順に反応し,\(\rm{Li}\)〜\(\rm{Al}\)まではイオンとして残ります!
陽極での反応についても簡単に説明しておくと,電極が\(\rm{Pt,Au}\),黒鉛以外の場合はその電極が反応し,それ以外であれば,溶液中に存在するハロゲンイオンが反応します.
この範囲については,またまとめますね!
このように周辺知識もしっかりと覚えるようにしましょう!時間をかけて復習するというのはこういうことです!
問4
まず電気分解で流れた電子e^-の物質量を求めていきましょう!
\(e^- = \large \frac{1.00\ ×\ 10^2\ ×\ 10^{-3}\ ×\ (32\ ×\ 60\ +\ 10)}{9.65\ ×\ 10^4} \small = 2\ \rm{mmol}\)
電気分解の分野では,電気量から分解される物質の物質量を求めるという計算方法があります.みなさんが覚えているのは,次の公式だと思います.
\(e^- = \large \frac{I\ ×\ t}{F}\)
\(I\):電流 \(\rm{[A]}\),\(t\):時間 \(\rm{[s]}\),\(F\):ファラデー定数
では,なぜこのような公式になるのでしょうか?
まず物理学より,電気量はクーロン(単位:\(\rm{C}\))という単位が用いられます.ここで,\(1\)クーロンとは,\(1\ \rm{A}\)の電流が\(1\ \rm{s}\)間に流れたときに運ばれる電気量のことです.つまり,
\(Q\ \rm{[C]} = \)\(I\ \rm{[A]}\ ×\ \)\(t\ \rm{[s]}\)
物理学ではクーロンという単位を用いていますが,化学の分野では一般的に物質量\(\rm{mol}\)を使用します.そのためクーロンから\(\rm{mol}\)へと変換する定数が必要となります.これがファラデー定数\(F\)です.ファラデー定数は\(F=9.65\ ×\ 10^4\ \rm{C/mol}\)となっていて,\(\rm{C}\)から\(\rm{mol}\)へ変換できることがわかると思います!
そのため,公式は次のようになるのです!.
\(e^- = \large \frac{Q}{F} \small = \large \frac{I\ ×\ t}{F}\)
また先程の計算結果で,「\(\rm{mmol}\)」という単位を使っています.これは「\(\rm{mg}\)」や「\(\rm{mL}\)」と同じような感覚で使っています.計算途中では,\(×\ 10^{-3}\)といちいち書いていては時間がかかって計算間違いも頻発してしまうため,「\(\rm{mmol}\)」を使っています!みなさんも使いこなせるようになってくださいね!
次に,問\(3\)の解答で求めたイオン反応式から\(\rm{H_2,Cl_2}\)がそれぞれ\(2\ \rm{mmol}\ ×\ \large \frac{1}{2} \small = 1\ \rm{mmol}\)発生していることがわかります.そのため\(\rm{H_2,Cl_2}\)の混合分圧である\(p_{\rm{H_2+Cl_2}}\)は,
\(p_{\rm{H_2+Cl_2}} = \large \frac{2\ ×\ 8.31\ ×\ 10^3\ ×\ (273\ +\ 27)}{3.00\ ×\ 10^{-2}} \small = 166 × 10^2\ \rm{Pa}\)
ここでも「\(\rm{mmol}\)」を使った小さなポイントが隠れています!
体積\(V\)の単位も「\(\rm{mL}\)」であるため,分母分子でそれぞれの「\(\rm{m}\)」を約分することができます.\(\rm{\large \frac{mmol}{mL} \small = \large \frac{mol}{L}}\)となり,\(10^{-3}\)を意味する「\(\rm{m}\)」が約分されています.このように計算が簡略化できるため,「\(\rm{mmol}\)」を使うメリットがあります.
最後に全圧として,空気の分圧\(p_{\rm{Air}}\)と\(p_{\rm{H_2+Cl_2}}\)を考えましょう.
\(全圧 = p_{\rm{Air}}\ +\ p_{\rm{H_2+Cl_2}} = (1013\ +\ 166)\ ×\ 10^2\ \rm{Pa} = 1179\ ×\ 10^2 \rm{Pa} = 1.2\ ×\ 10^4 \rm{Pa}\)
大問2(b)
大問\(2(\rm{b})\)は気相平衡に関する問題です.
今回もそれぞれの問題を解いていきながら,重要ポイントを徹底的に解説していきます.
問5
まずは図\(3\)の見方から解説していきましょう!
操作\(1\)で書かれているように,\(\rm{CO_2}\)と過剰の\(\rm{C}\)を反応器内に加えると,容器に入れた直後は,\(\rm{CO_2}\)のみとなります.そして自然と反応が右に進んでいき,\(\rm{CO}\)が少しずつ発生していきます.ある程度進んだところで平衡となり,その点が\(\rm{B}\)となります.さらに操作\(3\)で容器内の気体に圧力を加えていくと,矢印\(②\)の方向に平衡を保ったまま移動していきます.

このことから\(p_{\rm{CO_2}} = p_{\rm{CO}} = 1.0\ ×\ 10^5\ \rm{Pa}\)の点が平衡にのっていることがわかります.この曲線上の点は\(K_{\rm{p}} = \large \frac{(p_{\rm{CO}})^2}{p_{\rm{CO_2}}}\)の曲線上の点となります.これらの値を代入すると,
\(K_{\rm{p}} = \large \frac{100^2}{100} \small = 100\ \rm{kPa} = 1.0\ ×\ 10^5\ \rm{Pa}\)
となります.
\(K_{\rm{p}} = \large \frac{(p_{\rm{CO}})^2}{p_{\rm{CO_2}}}\)
この式を\(p_{\rm{CO}} = y,p_{\rm{CO_2}} = x\)とおいて考えてみましょう.すると,
\(K_{\rm{p}} = \large \frac{y^2}{x}\)
\(x = \large \frac{1}{K_{\rm{p}}}\ \small y^2\)
これをグラフにすると下のようになります.
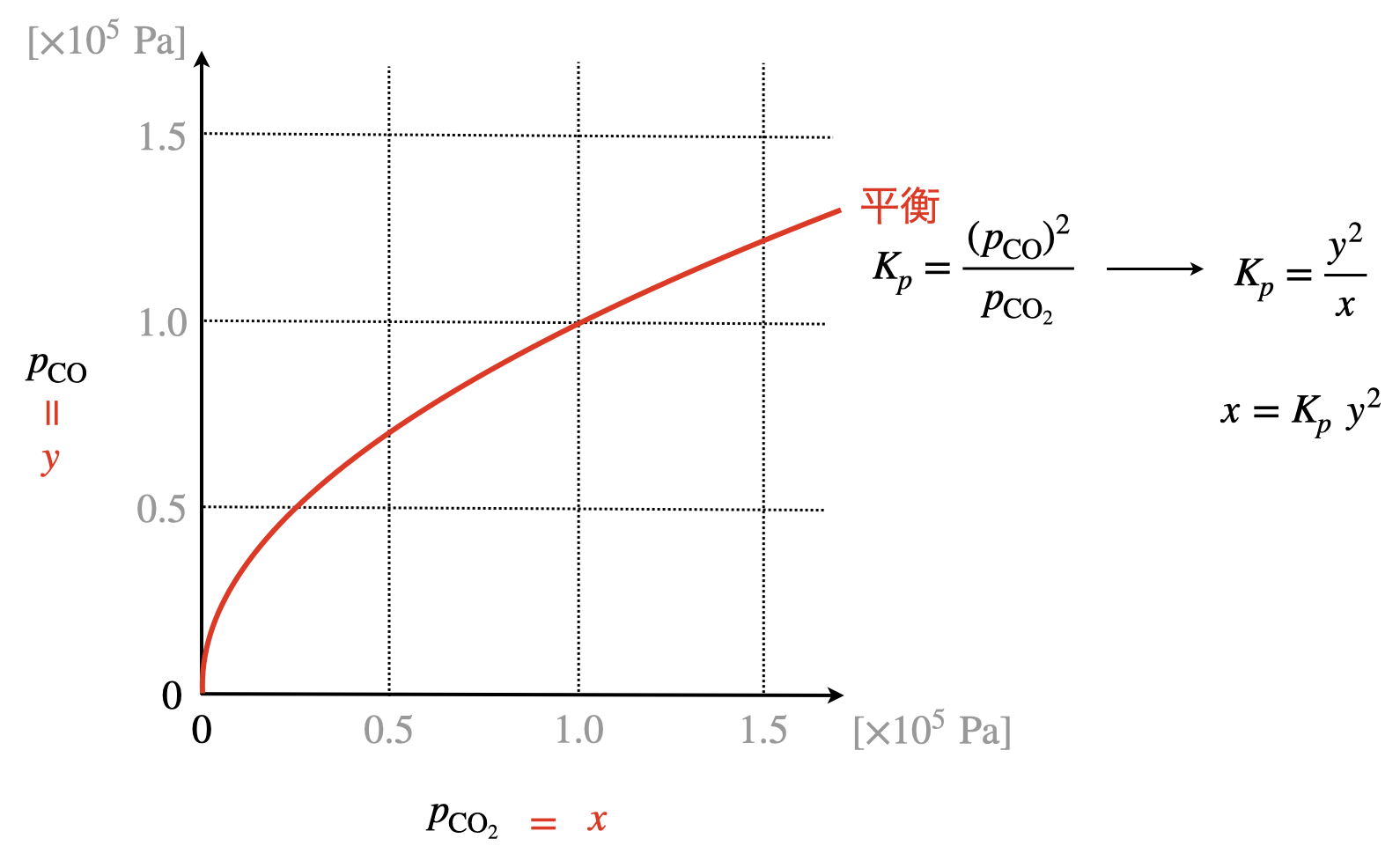
これは数学\(3\)で習う\(2\)次曲線ですね!このように数学の知識も使うとより理解が進むことがあります.随時紹介していきますね!
数式を扱うときに指数が出てくると,とても計算が面倒になる場合があります.そこで圧力の計算で有効になるのが,「\(\rm{kPa}\)」という単位です.ここで,「\(k\)」とは「\(×\ 10^3\)」という意味です.そのため,自分で「\(\rm{kPa}\)」という単位を使って解いて,最後に「\(\rm{Pa}\)」単位に直すというのでも全然OKです!どんどん使いこなしていきましょう!
以下の問題でも「\(\rm{kPa}\)」を使って計算すると計算間違いも少なくなり,スムーズに計算することができます!
問6
点\(\rm{A}\)から点\(\rm{B}\)へ移動する間,全圧は\(P_1\)で常に一定となっています.そして容器内には\(\rm{CO}\)と\(\rm{CO_2}\)しか含まれていないため,その和は常に\(P_1\)となります.
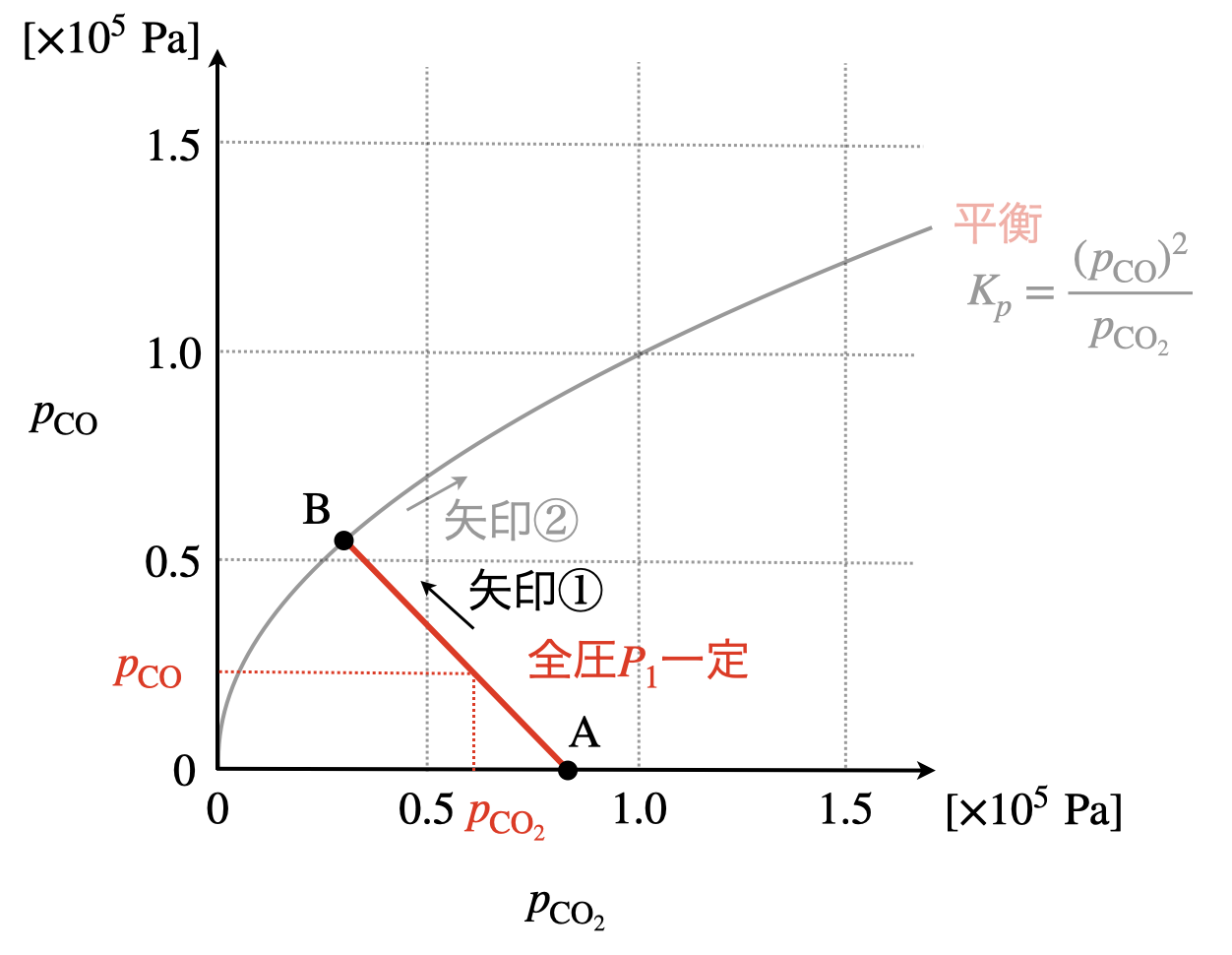
よって,
\(P_1 = p_{\rm{CO}} + p_{\rm{CO_2}}\)
問7
(ⅰ)
\((\rm{\hspace{.18em}i\hspace{.18em}})\)については,問\(5\)と問\(6\)の式を連立することで解くことができます.それではやっていきましょう!
\(K_{\rm{p}} = \large \frac{(p_{\rm{CO}})^2}{p_{\rm{CO_2}}} \small = 100\ \rm{kPa}\)
\(P_1 = p_{\rm{CO}} + p_{\rm{CO_2}} = 75\ \rm{kPa}\)
この問題では\(p_{\rm{CO}}\)を求める必要があるため,\(p_{\rm{CO_2}}\)を消去して解いていきましょう!
\(p_{\rm{CO_2}} = 75\ -\ p_{\rm{CO}}\)
これを第\(1\)式に代入します.
\(\large \frac{(p_{\rm{CO}})^2}{(75\ -\ p_{\rm{CO}})} \small = 100\)
こうすると,
\((p_{\rm{CO}})^2 + 100\ p_{\rm{CO}}\ -\ 7500 = 0\)
\((p_{\rm{CO}}\ -\ 50)(p_{\rm{CO}} + 150) = 0\)
\(p_{\rm{CO}} > 0\)なので,
\(p_{\rm{CO}} = 50\ \rm{kPa} = 5.0\ ×\ 10^4\ \rm{Pa}\)
となります.
(ⅱ)
問題文に「\(\rm{CO}\)の分圧と\(\rm{CO_2}\)の分圧が等しくなった」とあります.この点を\(\rm{C}\)とすると,図のようになります.

この図より,\(p_{\rm{CO}} = p_{\rm{CO_2}} = 100\ \rm{kPa}\)であることがわかります.よって,
\(P_2 = p_{\rm{CO}} + p_{\rm{CO_2}} = 100 + 100 = 200\ \rm{kPa}\)
\(\large \frac{P_2}{P_1} \small = \large \frac{200}{75} \small = \large \frac{8}{3}\)
(ⅲ)
まず,\(V_1\)から求めていきましょう!
最初に,容器内に加えた\(\rm{CO_2}\)の物質量を\(n\ \rm{mol}\)とします.すると,平衡移動し点\(\rm{B}\)に移動します.今までは圧力で考えていましたが,これを物質量で考えてみましょう.
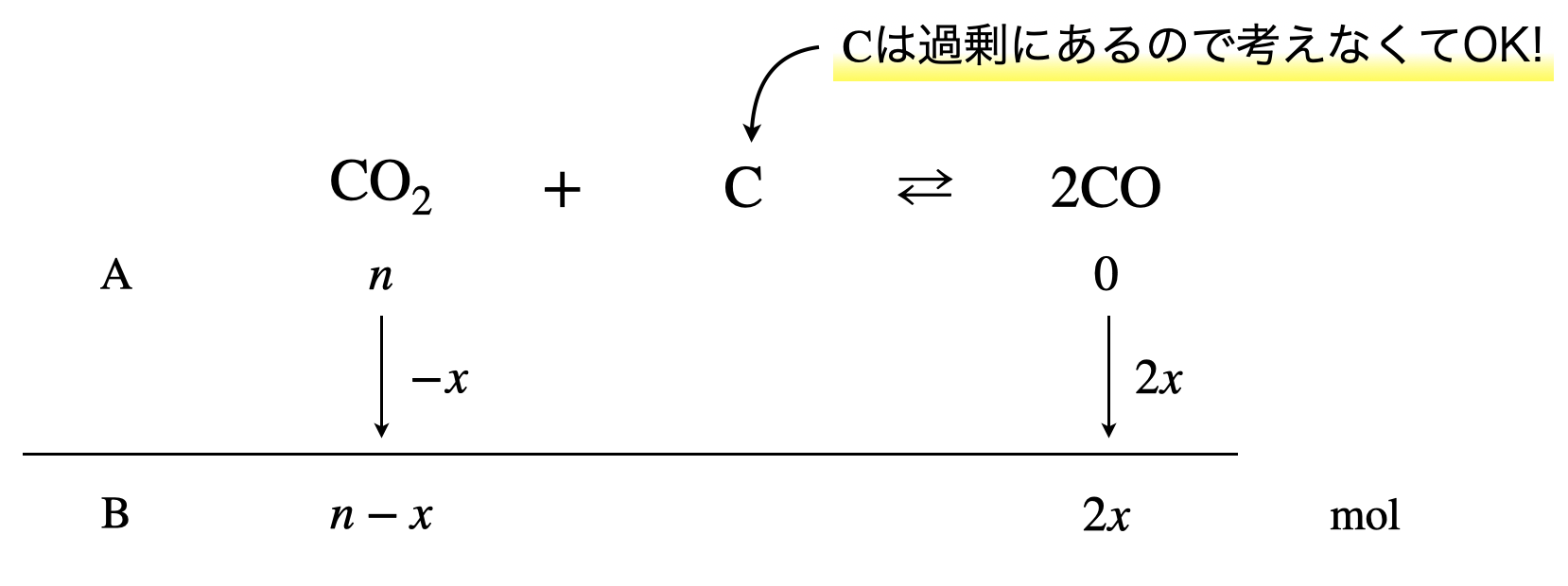
そしてこの容器内の物質に関して考えると,\(V,T\)が一定なので,\(p=kn\)となります.\((\rm{\hspace{.18em}i\hspace{.18em}})\)より,\(p_{\rm{CO_2}} = 25\ \rm{kPa},\)\(p_{\rm{CO}} = 50\ \rm{kPa}\)となるので,物質量もこの比になります.
\((n\ -\ x) : 2x = 1 : 2\)
\(x = \large \frac{1}{2}\ \small n\)
よって,点\(\rm{B}\)の全物質量は \((n – x) + 2x = n + x = \large \frac{3}{2}\ \small n \)となります.
次に,操作\(3\)後の平衡を図の\(\rm{C}\)の状態とします.この\(\rm{C}\)の状態について考えていきましょう.この場合,\(\rm{B\ →\ C}\)と考えてもよいですが,これだと少し複雑になってしまいます.単純に考えると,\(\rm{A}\)(\(\rm{CO_2}\)を\(n\ \rm{mol}\)加えた)\(→\ \rm{C}\)に到達したと考えることもできます.そして平衡移動し,全体として\(y\ \rm{mol}\)移動したとすると,先程の\(x\)が\(y\)に変化しただけということになります.
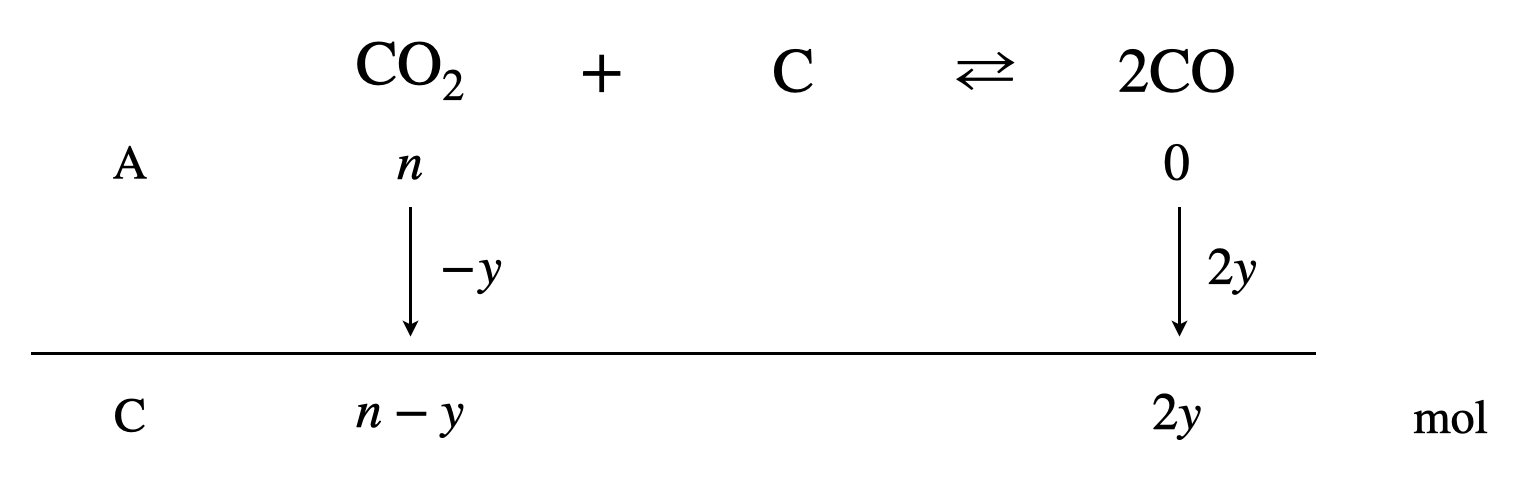
そして操作\(3\)に関しても\(V,T\)が一定なので,\(p=kn\)となります.
\(p_{\rm{CO_2}} = p_{\rm{CO}} = 100\ \rm{kPa}\)
なので,
\((n – y) : y = 1 : 1\)
\(y = \large \frac{1}{3}\ \small n\)
よって,点\(\rm{C}\)の全物質量は \((n – y) + 2y = n + y = \large \frac{4}{3}\ \small n \)となります.
最後に\(T\)一定なの,\(pV = kn\)となります.つまり,\(V = \large \frac{kn}{p}\)となります.
\(\large \frac{V_2}{V_1} \small = \large \frac{\left( \frac{n_2}{p_2} \right)}{\left( \frac{n_1}{p_1} \right)} \small = \large \frac{n_2}{n_1}\ \frac{p_1}{p_2} \small = \large \frac{\left( \frac{4}{3} n \right)}{\left( \frac{3}{2} n \right)}\ \frac{75}{200} \small = \large \frac{1}{3}\)
最後に
最後まで閲覧していただきありがとうございました.
今回の問題では,単位の取り扱いについても解説しました.「\(\rm{mmol}\)」や「\(\rm{kPa}\)」を使いこなせるようになることで,計算が圧倒的に早くなります.このブログでは積極的にこのような単位を使っているので,このブログを参考にぜひ使いこなせるようにしてくださいね!
本記事の内容についてわからない点があれば,遠慮なく質問していただければと思います.
(Twitter:chem_story1)
京都大学の化学は難問が多いと言われますが,その分多くのことを学ぶことができます.
皆さんの学習の一助になれば幸いです.
大問\(3\)についてはこちらをご覧ください!




コメント