
大問\(2\)の総評
こんにちは,\(\rm{KUT}\)です.
本記事では,\(2019\)年京大化学の大問\(2\)について解説していきます.
また解説に加えて,それぞれの問題で覚えておいてほしいポイントについて詳しく説明していきます.
京大の化学は難しいという印象が強い方が多いと思いますが,京大化学には難しい問題と標準問題の\(2\)つがあります.ここで,受験生が対策すべきことが\(2\)つあります.
\(1\)つ目は,標準問題を最後まで解き切る力を身につけることです.これにより,まずは平均点を取ることを目指します.
\(2\)つ目は,難しい問題と標準問題を見分けられる目を養うことです.試験本番は時間制限内に自分の解ける問題を解き切る必要があります.そのため,難しい問題は解かずに,標準問題をしっかりと選択していきながら,最後まで解いていくことが必要になります.
この記事では,問題を選択していく目を養うために,どのようにして判断していくのかということも自分なりに説明していきます.
それでは,\(2019\)年京大化学の大問\(2\)の解説に進んでいきましょう!
\(\rm{(a)}\)は,電子式や形の推定に関する問題です.自分のルーティーンで解けるかが「カギ」となります.
\(\rm{(b)}\)は,気体に関する平衡問題です.それぞれの考え方などを基礎からしっかりと解説していきます!
それでは今日も頑張っていきましょう!
大問\(2\)
(\(\rm{a}\))
\(\rm{(a)}\)は,分子に関する電子式や形の推定に関する問題でした.問\(1\)は身近な物質についてでしたが,問\(2\)は初見の物質だったと思います.初めてみる物質の形を推定する方法を丁寧に解説していきます.
問\(1\)
ア・イ
ここは今までの学習の復習ですね.電子対には\(2\)通りがあります.それは「分子間で電子対を共有しているかどうか」です.
- 共有しているもの→共有結合
- 共有していないもの→非共有結合
ここからが問\(1\)の本番となります.
ウ・エ
まずは,問\(1\)の条件を整理しましょう.
- 分子式:\(\rm{EZ_2\ or\ EZ_3}\)
- \(\rm{E \cdot Z}\)原子:\(\rm{C}\),\(\rm{H}\),\(\rm{O}\),\(\rm{N}\)のいずれか
上の条件かつ直線形の分子は,二酸化炭素(\(\rm{CO_2}\))です.
今回の問題に出てくる物質の電子式の書き方については,以下の記事ですべて解説しています.「秘伝の\(5\)ステップ」も紹介していますので,そちらをご覧ください!

\(\rm{CO_2}\)の電子式は次のようになります.
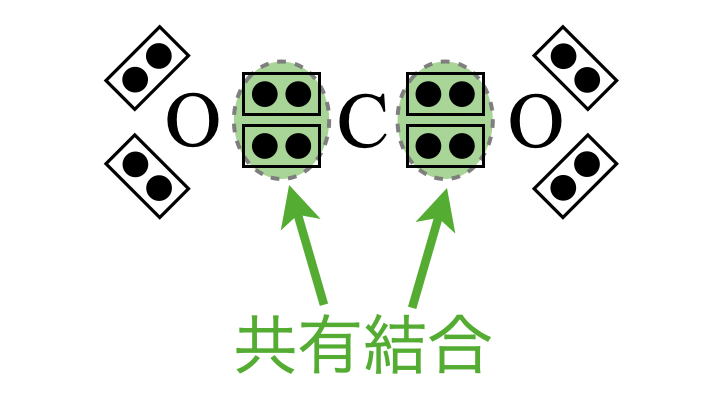
これから中心原子(\(\rm{C}\)原子)の周りの非共有電子対は\(0\)であることがわかります.
オ・カ
上の条件かつ折れ線形の分子は,水(\(\rm{H_2O}\))です.\(\rm{H_2O}\)の電子式は次のようになります.
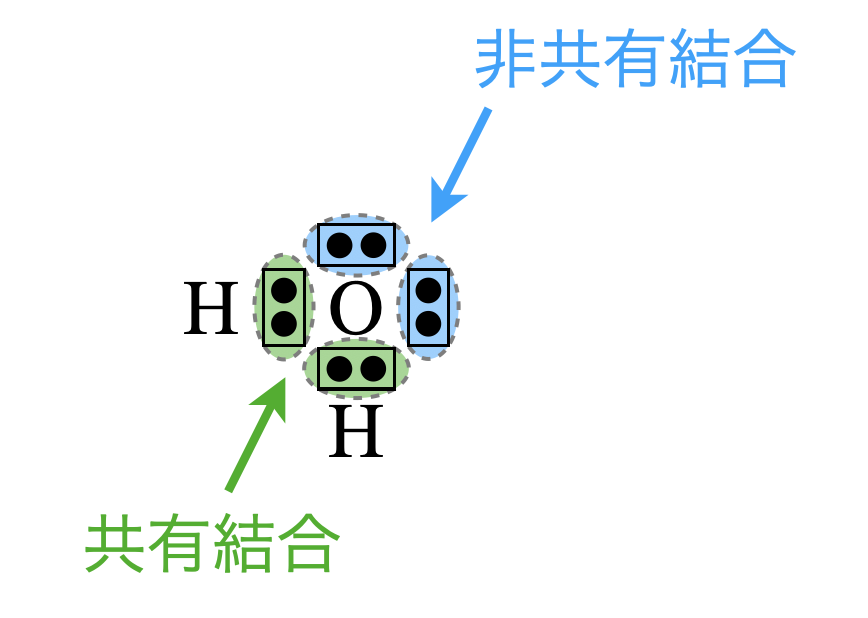
これから中心原子(\(\rm{O}\)原子)の周りの共有電子対は\(2\)であることがわかります.
キ・ク
物質についてはすでに問題で与えられています.メタン(\(\rm{CH_4}\))の電子式を示すと,次のようになります.
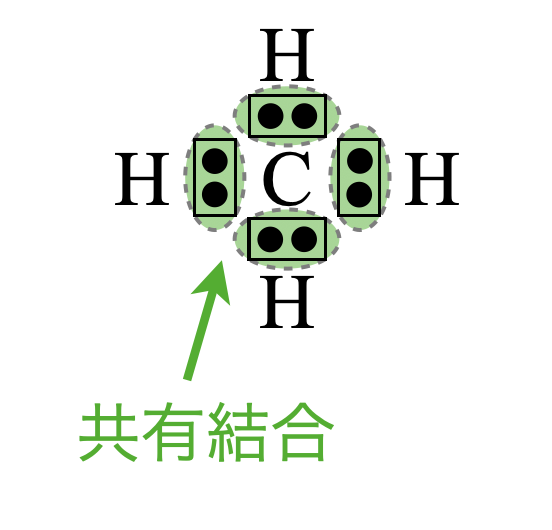
これから中心原子(\(\rm{C}\)原子)の周りの共有電子対は\(4\),共有電子対は\(0\)であることがわかります.
ケ・コ
上の条件かつ三角錐形の分子は,アンモニア(\(\rm{NH_3}\))です.アンモニア(\(\rm{NH_3}\))の電子式を示すと,次のようになります.
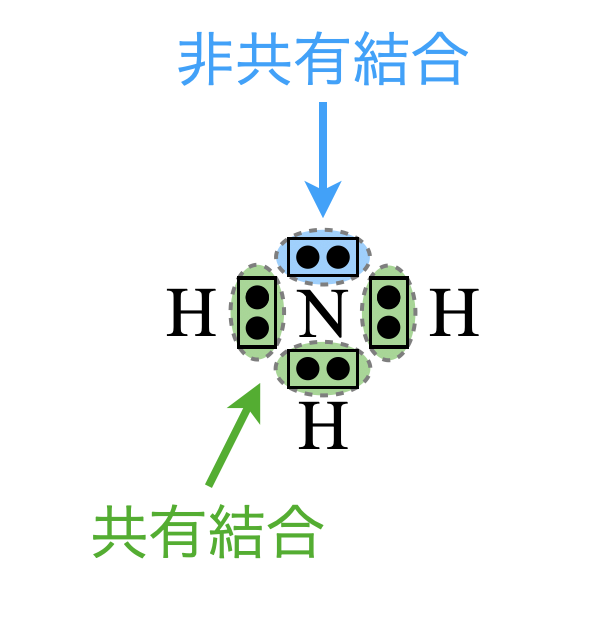
これから中心原子(\(\rm{N}\)原子)の周りの共有電子対は\(1\)であることがわかります.
問\(2\)
ニトロニウムイオン\(\rm{NO_2^+}\)の電子式を導くと同時に,形の推定をする問題です.
(\(1\))
まずは,ニトロニウムイオン\(\rm{NO_2^+}\)の電子式を導いていきます.
下のステップの順に解説していきます.
\(\rm{Step2:}\)周りの電子に\(8\)個電子を置き,その合計(\(y\))を求める
\(\rm{Step3:}\)足りない電子数(\(x\ – y\))を中心に配置する
\(\rm{Step4:}\)電子の調整をする
まず,それぞれ\(x\)と\(y\)を求めていきましょう.
\(\rm{NO_2^+}\)の場合は,\(x = 5 + 6 × 2\ – 1 = 16\)コ,\(y = 8 × 2 = 16\)コ
\(x\)をカウントするときには,陽イオンであるため,「\(\rm{-1}\)」を忘れないでくださいね!
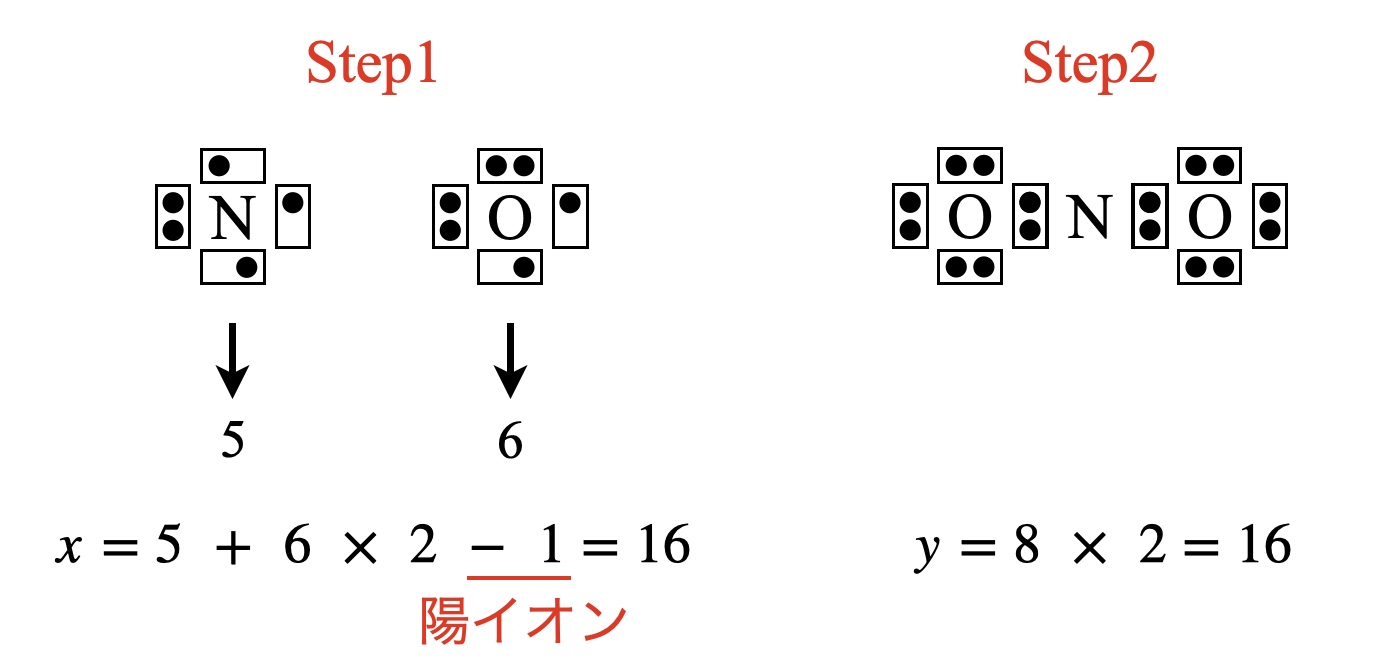
\(x\ – y = 16\ – 16 = 0\)なので,電子を追加する必要はありません.
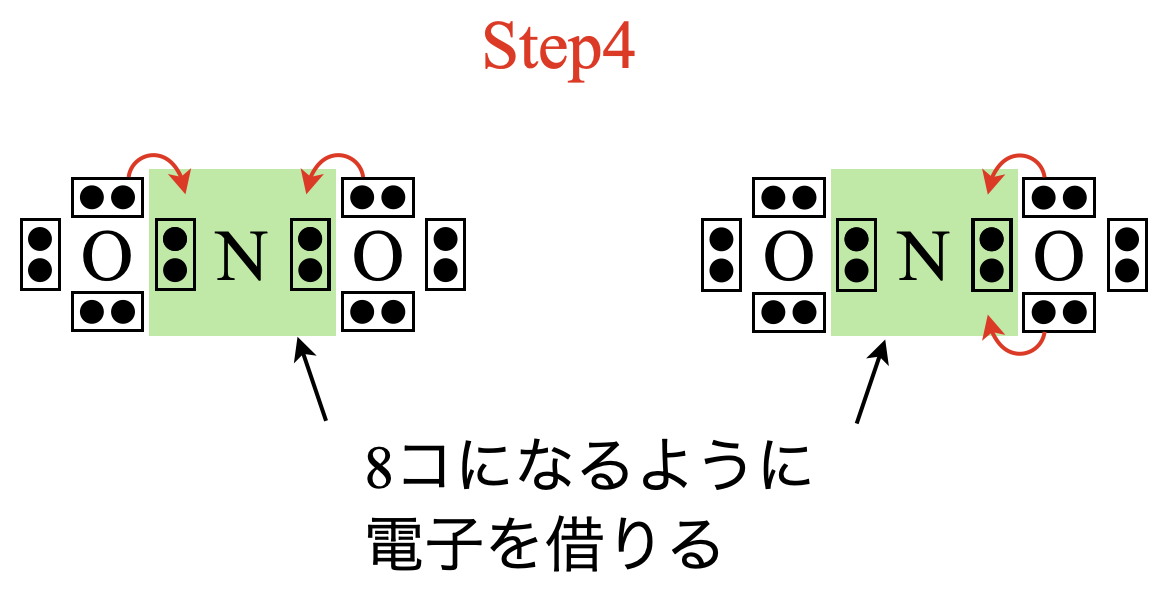
次のステップとして,\(\rm{N}\)原子の周りの電子数が\(8\)コとなるように\(\rm{O}\)原子から電子を\(4\)コ借りてくる必要があります.このとき左右の\(\rm{O}\)原子からそれぞれ\(2\)コずつ借りてくるパターンと,どちらかの\(\rm{O}\)原子から\(4\)コ借りてくるパターンの\(2\)つが考えられます.そのため今回は,いずれかを答えれば\(\rm{OK}\)です.
(\(2\))
次に,先ほどのニトロニウムイオン\(\rm{NO_2^+}\)の電子式をもとに形を推定していきましょう.
形の推定は以下の\(3\)ステップで行います.
\(\rm{Step2:}\)電子対が何カ所あるのか確認する
\(\rm{Step3:}\)電子対の配置を確認する
\(\rm{Step1}\)については,(\(1\))ですでに完了しています.
\(\rm{Step2 \cdot 3}\)
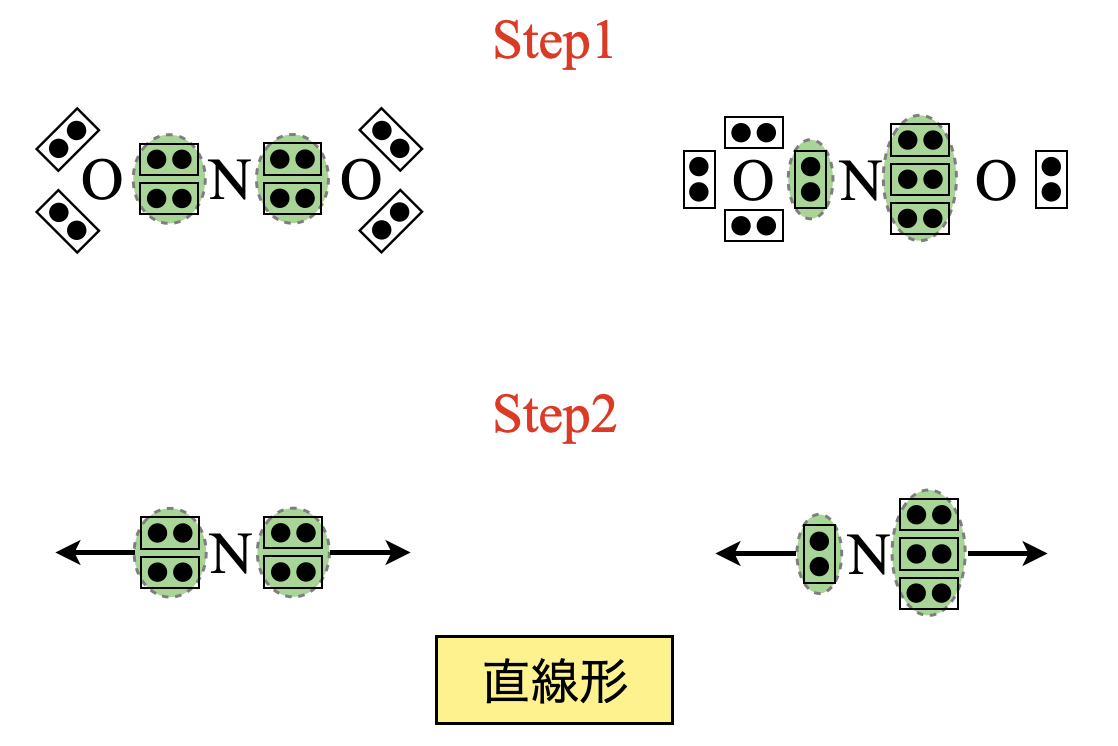
電子対のカ所を数えていきます.\(\rm{NO_2^+}\)は,いずれの電子式でも\(2\)カ所あることがわかります.そのため電子が反発しあって,直線形になります.
今回の問題は,電子式の導き方や形の推定がテーマでした.問\(1\)については暗記で対応できるかもしれませんが,問\(2\)のような初見の問題にも対応できるようにしっかりと解説した方法を自分のものにしておきましょう!
(\(\rm{b}\))
\(\rm{(b)}\)は気体平衡に関する問題です.問\(5\)に関しては少し複雑ですが,一緒に頑張っていきましょう!
問\(3\)
平衡定数に関する問題です.この式変形は参考書などに書かれていますが,まったく覚える必要はありません.覚えずに一瞬で導く方法をしっかりと解説していきます.
あ:濃度平衡定数\(K_{\rm{c}}\)
平衡定数の中で,濃度\(\rm{[X]}\)を使って表すものを濃度平衡定数といいます.
\(K_{\rm{c}} = \large \frac{\rm{[B]^2}}{\rm{[A]}}\)
と表せます.
い:圧平衡定数\(K_{\rm{p}}\)
まずは圧平衡定数\(K_{\rm{p}}\)を分圧\(p_{\rm{A}}\),\(p_{\rm{B}}\)で表します.
\(K_{\rm{p}} = \large \frac{p_{\rm{B}}^2}{p_{\rm{A}}}\)
ここで覚えておいてほしい式があります.それが\(p = CRT\)です.
この式は状態方程式:\(pV = nRT\)の両辺を\(V\)でわると,以下のように導けます.
\(p = \large \frac{n}{V} \small RT = CRT\)
たしかに\(\large \frac{n}{V}\)の単位が\(\rm{mol/L}\)になっていますね.
この式を使うと,すぐに式変形できます.
\(K_{\rm{p}} = \large \frac{p_{\rm{B}}^2}{p_{\rm{A}}} \small = \large \frac{(\rm{[B]} \it{RT})^2}{\rm{[A]} \it{RT}} \small = \large \frac{\rm{[B]}^2}{\rm{[A]}} \small RT = K_{\rm{c}}RT\)
う:モル分率平衡定数\(K_{\rm{x}}\)
モル分率については初めて見た方もいるかもしれませんので,ここで覚えてしまいましょう!
モル分率に関する定数で,以下の式になります.
\(K_{\rm{x}} = \large \frac{x_{\rm{B}}^2}{x_{\rm{A}}}\)
ここで,全圧を\(p\)とすると,それぞれの分圧は,\(p_{\rm{A}} = x_{\rm{A}} p\),\(p_{\rm{B}} = x_{\rm{B}} p\)となります.これを\(K_{\rm{x}}\)に代入しましょう.
\(K_{\rm{x}} = \large \frac{\left( \frac{p_{\rm{B}}}{p} \right)^2}{\frac{p_{\rm{A}}}{p}} \small = \large \frac{p_{\rm{B}}^2}{p_{\rm{A}}} \small \cdot \large \frac{1}{p} \small = \large \frac{K_{\rm{p}}}{p}\)
問\(4\)
え
容器内には\(\rm{A}\)と\(\rm{B}\)しか存在しません.そのため,\(x_{\rm{A}} + x_{\rm{B}} = 1\)となります.
その上で,本問にはさらに条件:\(x_{\rm{A}} = x_{\rm{B}}\)があります.
この\(2\)式を連立することで\(x_{\rm{A}}\),\(x_{\rm{B}}\)を求めることができます.
\(x_{\rm{A}} = x_{\rm{B}} = \large \frac{1}{2}\)
これをうに代入することで,答えを求めることができます.
\(K_{\rm{x}} = \large \frac{\left( \frac{1}{2} \right)^2}{\frac{1}{2}} \small = \large \frac{1}{2}\)
ただ,様々な状況の問題に対応するためには,感覚で解くのではなく,しっかりと理論を自分に染み込ませ,地に足をつきながら問題演習を行うことが非常に大切です.
答えがあってたからそのやり方はどうでもいいや,ではなくしっかりと理論を定着しながら演習を進めてくださいね!そのような受験生を心から応援していますよ!
お
かで求めた値をうに代入することで,簡単に求まります.
\(\large \frac{K_{\rm{p}}}{p} \small = \large \frac{1}{2}\)
\(p = 2 K_{\rm{p}}\)
問\(5\)
複雑な問題については,状況を整理してから解き進めましょう!
今回はモル分率が等しいという条件がありますが,モル分率では扱いづらいので,
モル分率が等しい→モルが等しい
と読みかえて解いていきましょう!
そのときの\(\rm{A}\)と\(\rm{B}\)の物質量を\(n\ \rm{[mol]}\)とします.すると,以下のように状況を整理することができます.

この問題を解き進めるにあたり,以下の\(3\)ステップで解説していきます!
\(\rm{Step2:}\)どの平衡定数を使うかを決める
\(\rm{Step3:}\)代入して計算する
\(\rm{Step1}\)
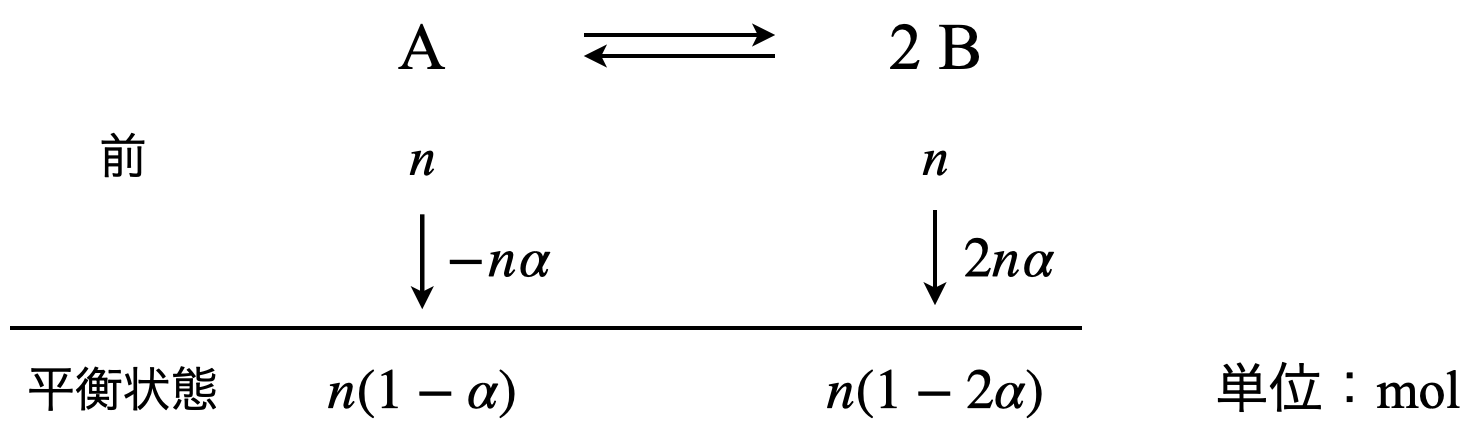
平衡後の物質量を求めるにあたり,ちょっとしたポイントがあります.
それが,「平衡後の物質量をどのように表すのか?」ということです.
表し方として,変化量を割合\(\alpha\)で表すか,それとも実際の物質量として表すかという\(2\)通りがあります.私としては前者の「変化量を割合\(\alpha\)で表す」方法がおすすめです.こちらの方がどのくらいの割合が変化したのかというのが瞬時にわかるので考えやすいです.
今回の操作では,容器の体積を大きくする,つまり圧力を下げるという操作を行いました.そのためルシャトリエの原理より平衡が右に移動することがわかります.その変化を表すと次のようになります.
\(\rm{Step2}\)
次に,どの平衡定数を使用するかを決定しましょう.平衡定数として使えるものは\(K_{\rm{c}}\),\(K_{\rm{p}}\),\(K_{\rm{x}}\)の\(3\)つがあります.
問\(3\)より,\(K_{\rm{c}}\),\(K_{\rm{p}}\)については温度\(T\)だけに依存する定数ですが,\(K_{\rm{x}}\)は温度\(T\)と圧力\(p\)に依存する定数であることがわかります.この場合,\(T\)一定なので,\(K_{\rm{c}}\),\(K_{\rm{p}}\)のいずれかで考えた方が簡単であることがわかります.
今回は物質量で考えているため,\(K_{\rm{c}}\)で考えてみましょう!ただし,\(K_{\rm{p}}\)で考えても同じように計算することができます.
\(\rm{Step3}\)
温度\(T\)一定なので,コックを開く前と後で\(K_{\rm{c}}\)の値は一定です.
コックを開く前は,体積が\(V_1\),開いた後は\(3V_1\)に変化していることに注意して立式していきましょう.
\(K_{\rm{c}} = \large \frac{\left( \frac{n}{V_1} \right)^2}{\frac{n}{V_1}} \small = \large \frac{\left( \frac{n(1 + 2 \alpha)}{3V_1} \right)^2}{\frac{n(1-\alpha)}{3V_1}}\)
これを整理すると,
\(4\alpha^2 + 7\alpha -2 =0\)
\((4\alpha -1 )(\alpha + 2) = 0\)
\(\alpha = \large \frac{1}{4}\)
新たな平衡状態における\(\rm{A}\)の物質量は\(n(1 – \alpha) = \large \frac{3}{4} \small n\ \rm{[mol]}\)なので,コックを開く前の\(\large \frac{3}{4}\)倍になっていることがわかります.
最後に
最後まで閲覧していただきありがとうございました.
今回の問題は,分子の電子式や形の推定をしっかりと行うことができるかが「カギ」でした.また平衡に関しては,京大でも頻出の分野なので,様々なパターンの問題にトライしていきましょう!このサイトでも随時様々なパターンを紹介していきます.一緒にレベルアップしていきましょう!
本記事の内容についてわからない点があれば,遠慮なく質問していただければと思います.
(\(\rm{Twitter}\):chem_story1)
京都大学の化学は難問が多いと言われますが,その分多くのことを学ぶことができます.
皆さんの学習の一助になれば幸いです.



コメント