
解説してほしい分野があればぜひ次の記事のコメント欄で教えてくださいね!

YouTubeでも解説動画を上げているので、ぜひご覧ください!
今回の全体的な流れについて簡単に説明します!
まず,水に溶けるという意味を解説していきます!溶解と一言でいっても化学溶解と物理溶解があります.
この違いについて説明したのち,いよいよヘンリーの法則について解説していきます.そしてヘンリーの法則の本質を理解した後,より考えやすいようにヘンリーの新公式を解説します.このヘンリーの新公式を使って私は受験を乗り切りました!
最後に,ヘンリーの新公式を使って,実際に練習問題を解いていき,理解を深めていきましょう!
溶解について
溶質が水和すると溶質は水に溶解します.

気体の水への溶解は,化学溶解と物理溶解の\(2\)通りがあります.
化学溶解とは,溶質(=気体分子)が水和状態になるのに,気体分子が水と化学反応を起こして親水性のイオンになることです.そして物理溶解とは,気体分子が弱い力であるファンデルワールス力だけで水和することです.それぞれについて,簡単にみていきましょう.
化学溶解
化学溶解では,水と反応すると親水性のイオンに変化するため,水に対する溶解性は大きくなります.これには\(\rm{NH_3}\)や\(\rm{HCl}\)が当てはまります.
\(\rm{NH_3}\)や\(\rm{HCl}\)はともに,水との反応でイオンとなります.イオンは極性分子である\(\rm{H_2O}\)と「似たもの同士」で溶けやすくなります!
物理溶解
気体が水に溶解する際,水とは化学反応せずに弱い力であるファンデルワールス力で水と水和する溶解法です.これは\(\rm{NH_3}\)や\(\rm{HCl}\)以外の気体に当てはまると考えましょう!
ヘンリーの法則
それではいよいよヘンリーの法則(\(\rm{Henry’s\ law}\))について説明していきます!
ヘンリーの法則を一言で言えば,
「水に溶けにくい気体の溶解度は気体の分圧に比例する」
ということです.
式にすると,下のようになります.
\(\rm{[A]} = \)\(kp_{\rm{A}}\)
ここで,\(k\):\(\rm{Henry}\)定数で,温度が一定の場合,\(k\)も一定です.

ここでの注意点は,この公式は\(\rm{NH_3}\)・\(\rm{HCl}\)については成立しないということです!
証明:ヘンリーの法則
それでは,ヘンリーの法則がなぜ成立するのかを考えていきましょう!
\(\rm{A}\)という気体が溶解平衡に到達しているとします.その関係を表すと,下のようになります.
\(\rm{A(g) ⇄ A(l)}\)
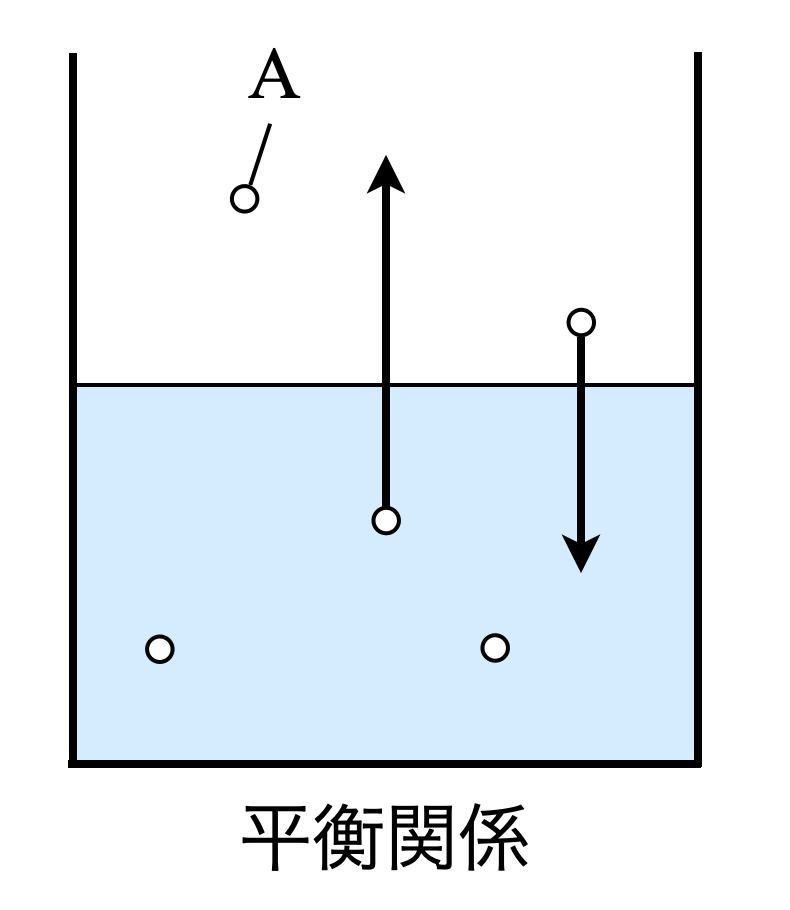
この平衡式の平衡定数を\(K\)とすると,
\(K = \large \rm{\frac{[A(l)]}{[A(g)]}}\)
\(\rm{[A(l)] =}\)\(K \rm{[A(g)]}\)
ここで\(\rm{[A(g)]}\)とは気体であるため,気体の状態方程式:\(pV = nRT\)を用いて表すことができます!
\(\rm{[A(g)]} =\)\(\large \frac{n_{\rm{A}}}{V} \small = \large \frac{p_{\rm{A}}}{RT}\)
これより上の式は以下のように変換できます.
\(\rm{[A(l)]} =\)\(K \rm{[A(g)]} =\)\( K \large \cdot \frac{p_{\rm{A}}}{RT} \small = \large \frac{K}{RT} \cdot \small p_{\rm{A}} = k p_{\rm{A}}\)
最後の変換では,\(\large \frac{K}{RT}\)が定数であるため,\(k\)としています!
ヘンリーの法則と温度の関係
ヘンリーの法則と温度の関係についても理解しておきましょう!
水の温度が上昇すると,溶解した気体粒子の運動エネルギーが増加します.そのため,ファンデルワールス力で水和した水分子を振り切って水の外部に出ていく力が働きます!その結果,水の温度が上昇すると,気体の溶解度は減少することになります.

これはつまり,
「温度が上昇すると,\(\rm{Henry}\)定数:\(k\)の値が減少する!」
ということです!
ヘンリーの法則の問題点
ヘンリーがこの法則を発見した当時,物質量(モル)という概念はまだありませんでした.そのため,モルの代わりに水に溶解する前の気体の体積で溶解量を表現しました.
この点がヘンリーの法則をわかりにくくしている点になります.
体積で表現する場合,圧力・温度の条件によって変化するため,\(2\)通りの表し方があります.
標準状態での測定
溶解する気体の体積は,標準状態(=定圧・定量)の場合気体の分圧に比例します.
これは以下のように考えるとわかりやすいです!
ヘンリーの法則の公式より,気体の溶解量\(n_{\rm{A}}\ \rm{[mol]}\)は\(\rm{A}\)の分圧\(p_\rm{A}\ \rm{[kPa]}\)に比例します.
\(\rm{[A(l)]} =\)\(\large \frac{n_{\rm{A}}}{V_{\rm{H_2O}}} \small = k p_{\rm{A}}\)
この公式より,\(\rm{A}\)の分圧が\(2\)倍となると,気体の溶解量\(n_{\rm{A}}\)も\(2\)倍に増加します.
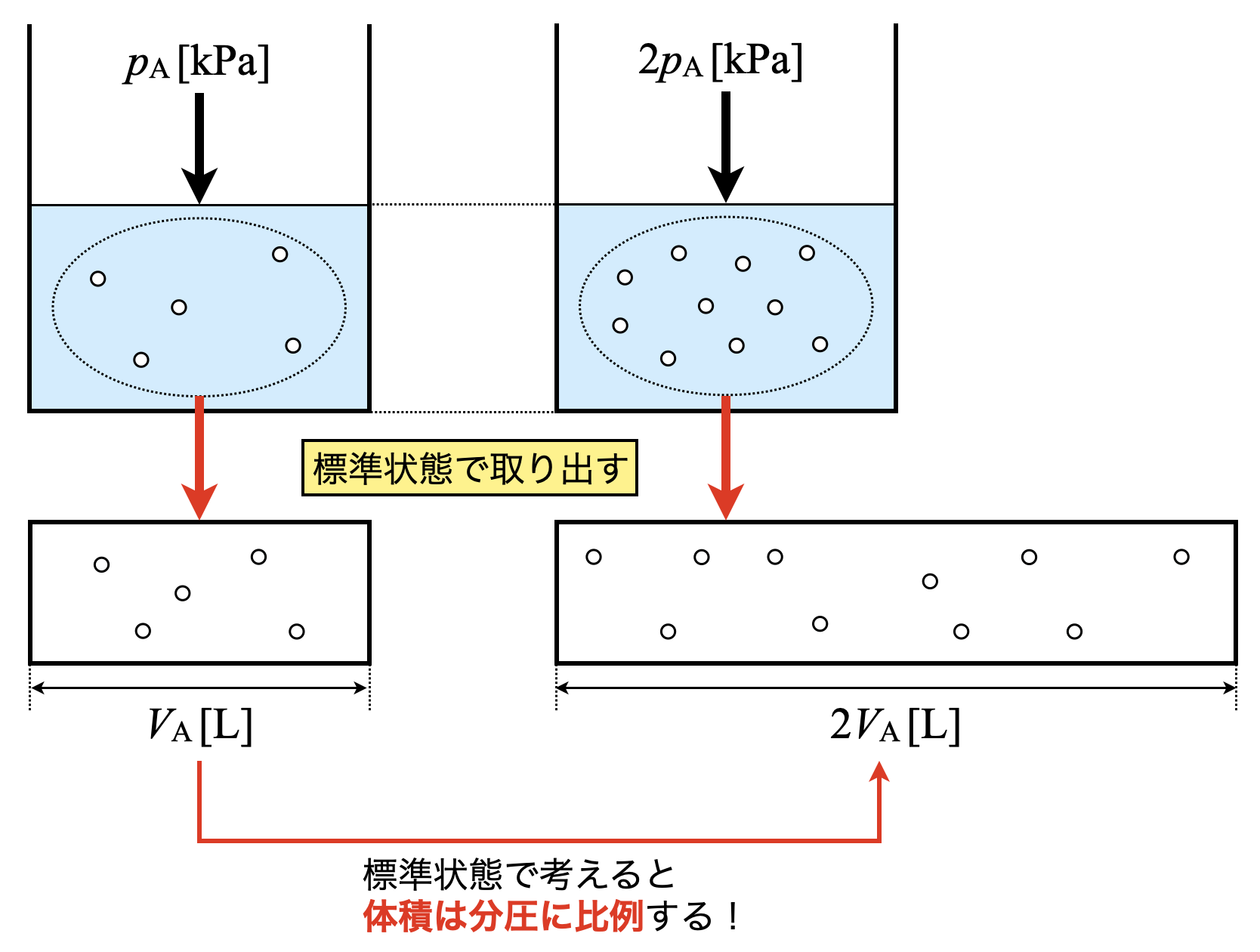
ここで,気体\(\rm{A}\)を標準状態の体積\(V_{\rm{A}}\ \rm{[L]}\)で考えてみましょう.気体の溶解量を\(n_{\rm{A}}\ \rm{[mol]}\)とすると,
\(V_{\rm{A}} = 22.4 n_{\rm{A}}\ \rm{[L]}\)
となります.そのため,\(n_{\rm{A}}\)も\(2\)倍となるため,\(V_{\rm{A}}\)も\(2\)倍となります.
これを図で整理すると以下のようになります.
溶解時の圧力での測定
溶解時の圧力で気体を測定すると,体積一定となります.このとき,溶解する気体の物質量(モル)は分圧に比例して増加しています.
これについても以下のように考えることで理解することができます.
気体\(\rm{A}\)を\(T\ \rm{[K]}\)において,分圧\(p_{\rm{A}}\ \rm{[kPa]}\),\(2p_{\rm{A}}\ \rm{[kPa]}\)にて溶解した場合を考えます.
① 分圧\(p_{\rm{A}}\ \rm{[kPa]}\)のとき
溶解していた\(n_{\rm{A}}\ \rm{[mol]}\)を取り出し,\(T\ \rm{[K]}\),\(p_{\rm{A}}\ \rm{[kPa]}\)での体積を\(V_1\ \rm{[L]}\)とすると,
\(V_1 = \large \frac{nRT}{p} \small = \large \frac{n_{\rm{A}}RT}{p_{\rm{A}}}\)
② 分圧\(2p_{\rm{A}}\ \rm{[kPa]}\)のとき
溶解していた物質量は\(2n_{\rm{A}}\ \rm{[mol]}\)となります.そのため溶解していた\(2n_{\rm{A}}\ \rm{[mol]}\)を取り出し,\(T\ \rm{[K]}\),\(2p_{\rm{A}}\ \rm{[kPa]}\)での体積を\(V_2\ \rm{[L]}\)とすると,
\(V_2 = \large \frac{nRT}{p} \small = \large \frac{2n_{\rm{A}}RT}{2p_{\rm{A}}} = \frac{n_{\rm{A}}RT}{p_{\rm{A}}}\)
これより\(V_1 = V_2\)となり,溶解時の圧力で測定すると,共に体積は等しくなります!

ヘンリーの新公式
今まで,ヘンリーの法則の本質について見てきました.頭がこんがらがっている人も多いのではないでしょうか?私も受験生時代はなにか魔法にでもかかったような気分になりました…笑
ヘンリーの法則がこんなに困難する理由はズバリ体積を用いて考えているからです!
みなさんは物質量(モル)を使って考えることができるため,物質量(モル)を使うことでスッキリと理解することができます!

これは今までに考えてきたモデルと全く同じものです.
\(\rm{[A(l)]} = \)\(\large \frac{n_{\rm{A}}}{V_{\rm{H_2O}}} \small = kp_{\rm{A}}\)
この式から溶解している物質量(モル)を求めることができます.
\(n_{\rm{A}} = kp_{\rm{A}}V_{\rm{H_2O}}\)
これがヘンリーの新公式になります!
① 物質量(モル)で考えることができる
この公式の\(1\)番の利点は,物質量(モル)で考えることができる点です!圧力を\(2\)倍にすれば,溶解する物質量も\(2\)倍になるというのは,直感的で理解しやすいですよね!
② 水の体積\(V_{\rm{H_2O}}\)をかけ忘れを防げる
\(n_{\rm{A}} = kp_{\rm{A}}V_{\rm{H_2O}}\)と公式を覚えておくと,水の体積\(V_{\rm{H_2O}}\)のかけ忘れを防ぐことができます!
ヘンリーの新公式を使う上での注意点が\(1\)つあります.
それは,\(\rm{Henry}\)定数:\(k\)を自分で求める必要があるという点です.入試問題では\(k\)は与えられていないため,自分で図を書きながら求め,その値を応用して問題を解いていきましょう!
練習問題
それではヘンリーの新公式を覚えたところで練習問題を解きながら使いこなせるようにしていきましょう!
気体\(\rm{A}\)の水への溶解にはヘンリーの法則が成り立つとする.
ある温度において,\(1.0P_0\ \rm{[Pa]}\)下で\(3.0V_0\ \rm{[L]}\)の気体\(\rm{A}\)を純水とともに容積可変の密閉容器内に入れた.圧力を\(1.0P_0\ \rm{[Pa]}\)に保つと,容器内の気体が占める体積は\(2.0V_0\ \rm{[L]}\)となった.この後,同じ温度で容器内圧力を\(0.50P_0\ \rm{[Pa]}\)に保った.
(\(1\))このときの容器内の気体が占める体積は何\(\rm{L}\)となるか?
(\(2\))容器内の水は\(0.50P_0\ \rm{[Pa]}\)で何\(\rm{L}\)に相当する量の気体が溶解しているか?
まずはこの問題の概要を掴む必要があります.
温度\(T\)は常に一定であるため,状態方程式:\(pV = nRT\)より,
\(\large \frac{pV}{n} \small = RT = K\)(一定)
となります.
それからヘンリーの新公式を使って,溶解している気体\(\rm{A}\)の物質量を求めていきましょう!
「\(1.0P_0\ \rm{[Pa]}\)下で\(3.0V_0\ \rm{[L]}\)の気体\(\rm{A}\)を水に押し込むと,容器内の気相体積が\(2.0V_0\ \rm{[L]}\)となった.」
という情報が問題文にあります.
加えた気体の物質量を\(3n_0\ \rm{[mol]}\)とし,このときの水の体積を\(V_{\rm{H_2O}}\ \rm{[L]}\),溶解した物質量を\(n_0\ {\rm{[mol]}}\)とすると,
\(n_0 = kP_0V_{\rm{H_2O}}\)
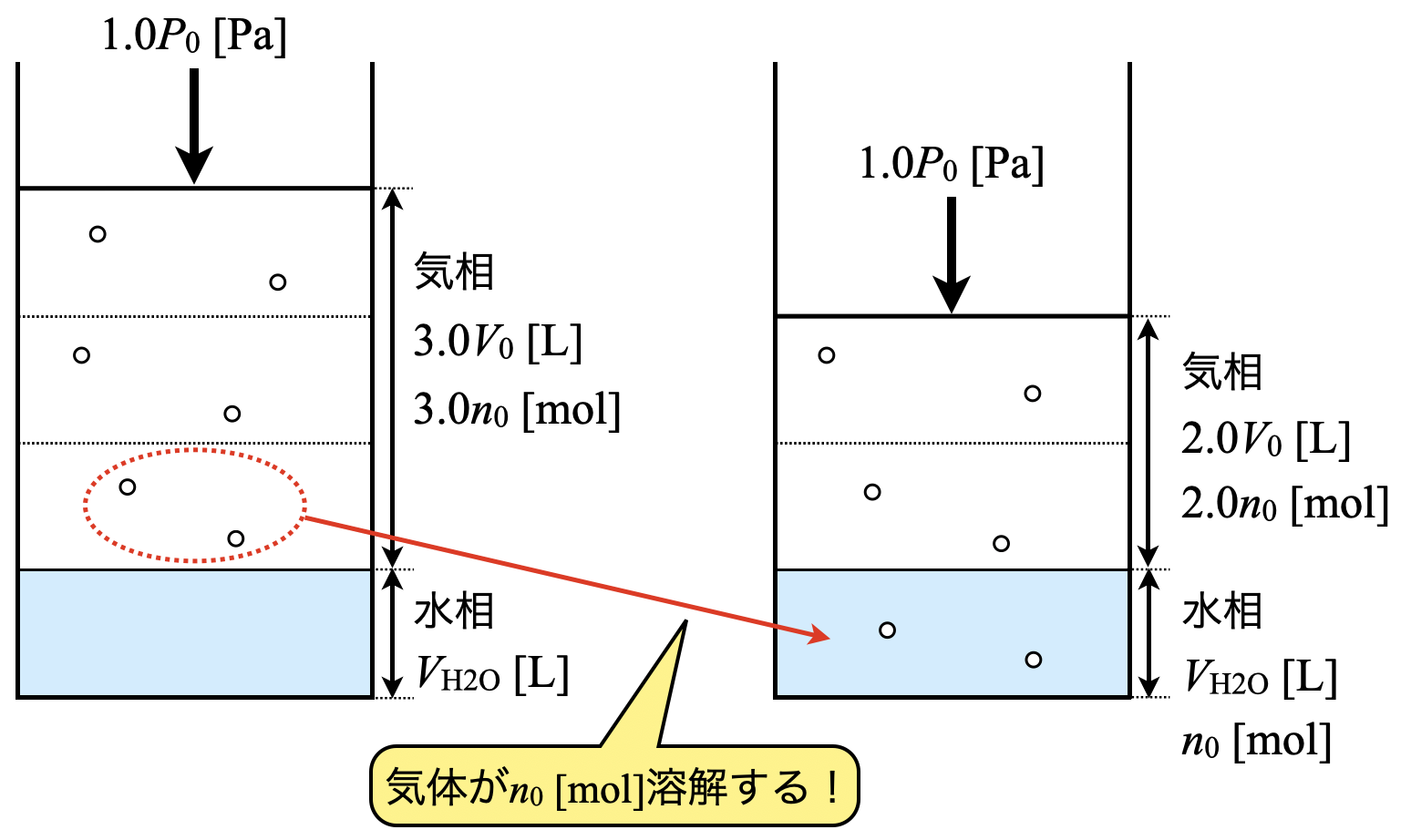
ここまでで準備は万端です!
それでは各設問を解いていきましょう!
(\(1\))
本問では水の体積:\(V_{\rm{H_2O}}\ \rm{[L]}\)が不変であり,全圧のみが\(1.0P_0\ \rm{[Pa]}\ →\ \)\(0.50P_0\ \rm{[Pa]}\)に変化していることになります.そのため,水に溶解した\(\rm{A}\)の物質量も\(0.5n_0\ \rm{[mol]}\)となります.
これはヘンリーの新公式を見ると,一目瞭然ですね!
\(n_0 = kP_0V_{\rm{H_2O}}\)
気相,水相の物質量の総和は\(3n_0\ \rm{mol}\)であるため,気相に残った物質量は
\(3n_0\ -\ 0.5n_0 = 2.5n_0\ \rm{[mol]}\)
となります.

このときの気相の体積を\(V_1\ \rm{[L]}\)とすると,
\(\large \frac{P_0 \cdot 3V_0}{3n_0} \small = \large \frac{0.5P_0 \cdot V_1}{2.5n_0} \small = K\)
\(V_1 = 5V_0\ \rm{[L]}\)
と求めることができました.
(\(2\))
水相に溶けた気体の体積を\(V_2\ \rm{[L]}\)とすると,(\(1\))と同条件であるためその体積は物質量に比例します.\(pV = nRT\)において,\(p\),\(T\)一定であるため,
\(V = \large \frac{RT}{p} \small × n \)
気相に残った気体の物質量の\(\large \frac{1}{5}\)が水相に溶けているため,\(V_2\ \rm{[L]}\)も\(V_1\ \rm{[L]}\)の\(\large \frac{1}{5}\)となります.
よって,
\(V_1 = 5 × \large \frac{1}{5} \small = 1.0 V_0\ \rm{[L]}\)
気体\(\rm{B}\)の水への溶解にはヘンリーの法則が成り立つとする.気体定数は\(R = 8.31 × 10^3\ \rm{Pa \cdot L/(mol \cdot K)}\)とする.
気体\(\rm{B}\)は\(1.00 × 10^5\ \rm{Pa}\)のとき,\(\rm{20^\circ C}\)の水\(1\ \rm{L}\)に\(1.39 × 10^{-3}\ \rm{mol}\),\(\rm{60^\circ C}\)の水\(1\ \rm{L}\)に\(8.70 × 10^{-4}\ \rm{mol}\)溶解する.容積\(1.100\ \rm{L}\)の容器に水\(1.000\ \rm{L}\)と気体\(\rm{B}\)を加えた.容器を\(\rm{20^\circ C}\)に保つと,容器内の気体\(\rm{B}\)の分圧は\(1.00 × 10^5\ \rm{Pa}\)となった.
(\(1\))この容器に加えた気体\(\rm{B}\)の物質量はいくらになるか?
(\(2\))容器を\(\rm{60^\circ C}\)まで昇温させ放置すると,容器内の気体\(\rm{B}\)の分圧はいくらになるか?
今回の問題は\(\rm{20^\circ C \cdot 60^\circ C}\)という\(2\)つの温度が存在します.\(\rm{Henry}\)定数は温度で一定であるため,それぞれの温度における\(\rm{Henry}\)定数を求める必要があります.

①\(\rm{20^\circ C}\)における\(\rm{Henry}\)定数:\(k_{20}\)
「気体\(\rm{B}\)は\(1.00 × 10^5\ \rm{Pa}\)のとき,\(\rm{20^\circ C}\)の水\(1\ \rm{L}\)に\(1.39 × 10^{-3}\ \rm{mol}\)溶解する」という条件をヘンリーの新公式に当て当てはめます.
\(n_{\rm{B}} = k_{20} p_\rm{B} V_{\rm{H_2O}}\)
\(1.39 = k_{20} × 100 × 1.000\)
\(k_{20} = 0.0139\ \rm{mmol/(kPa \cdot L)}\)
ここで,\(\rm{Henry}\)定数に「\(\rm{mmol}\)」と「\(\rm{kPa}\)」という単位を使っています!これが後ほどの計算で大活躍します!
②\(\rm{60^\circ C}\)における\(\rm{Henry}\)定数:\(k_{60}\)
「気体\(\rm{B}\)は\(1.00 × 10^5\ \rm{Pa}\)のとき,\(\rm{60^\circ C}\)の水\(1\ \rm{L}\)に\(8.70 × 10^{-4}\ \rm{mol}\)溶解する」という条件をヘンリーの新公式に当て当てはめます.
\(0.870 = k_{60} × 100 × 1.000\)
\(k_{60} = 0.00870\ \rm{mmol/(kPa \cdot L)}\)
ここまでで準備万端です!それでは各設問を解いていきましょう!
(\(1\))
本問の条件を図示すると以下のようになります.

これより気相と水相にわけて考える必要があります.気相については状態方程式:\(pV = nRT\),水相についてはヘンリーの新公式:\(n = kpV_{\rm{H_2O}}\)を使います.
それでは気相から求めていきましょう!
気体定数\(R = 8.31 × 10^3\ \rm{Pa \cdot L/(mol \cdot K)}\)を変形して,\(R = 8.31\ \rm{kPa \cdot L/(mol \cdot K)}\)として考えましょう!すると,\(p:\rm{kPa}\),\(V:\rm{mL}\),\(R:\rm{kPa \cdot L/(mol \cdot K)}\),\(T:\rm{K}\)であるため,\(n:\rm{mmol}\)という単位になります!
\(n:\large \rm{\frac{kPa\ \cdot\ mL}{\frac{kPa\ \cdot\ L}{mol\ \cdot\ K}\ \cdot\ K} \small = mmol}\)
このように単位を自在に使いこなせるようになりましょう!
\(n \rm{(g)} = \)\(\large \frac{pV}{RT} \small = \large \frac{100\ ×\ 100}{8.31\ ×\ (273\ +\ 20)} \small = 4.107\ \rm{mmol}\)
次に,ヘンリーの新公式を使って水相の気体\(\rm{B}\)の物質量を求めましょう!
\(n \rm{(l)} = \)\(k_{20} p_{\rm{B}} V_{\rm{H_2O}}\)
ここでの単位については,\(k:\rm{mmol/(kPa \cdot L)}\),\(p:\rm{kPa}\),\(V:\rm{L}\)であるため,\(n:\rm{mmol}\)となります.
\(n:\rm{\large \frac{mmol}{kPa\ \cdot\ L} \small \cdot kPa \cdot L = mmol}\)
\(n \rm{(l)} = \)\(0.0139\ ×\ 100\ ×\ 1.000 = 1.39\ \rm{mmol}\)
よって,気体\(\rm{B}\)の物質量の合計は
\(4.107\ +\ 1.39 = 5.497\ \rm{mmol} = 5.5 × 10^{-3}\ \rm{mol}\)
(\(2\))
(\(1\))と考え方は同じです!\(\rm{60^\circ C}\)における気体\(\rm{B}\)の気相の圧力を\(p\ \rm{[kPa]}\)として解いていきましょう.今回も気相と水相にわけて考えていきます.

それでは気相から求めていきましょう!
\(p:\rm{kPa}\),\(V:\rm{L}\),\(R:\rm{kPa \cdot L/(mol \cdot K)}\),\(T:\rm{K}\)であるため,\(n:\rm{mmol}\)という単位になります!毎回単位の確認はしてくださいね!
\(n \rm{(g)} = \)\(\large \frac{pV}{RT} \small = \large \frac{p\ ×\ 100}{8.31\ ×\ (273\ +\ 60)} \small = 0.036137p\ \rm{mmol}\)
次に,ヘンリーの新公式を使って水相の気体\(\rm{B}\)の物質量を求めましょう!
\(n \rm{(l)} = \)\(k_{20} p_{\rm{B}} V_{\rm{H_2O}}\)
\(k:\rm{mmol/(kPa \cdot L)}\),\(p:\rm{kPa}\),\(V:\rm{L}\)であるため,\(n:\rm{mmol}\)となります.
\(n \rm{(l)} = 0.00870\ ×\ p\ ×\ 1.000 = 0.00870p\ \rm{mmol}\)
気相と水相の合計は,先ほど(\(1\))で求めた\(5.497\ \rm{mmol}\)になるので,
\(0.036137p\ +\ 0.00870p = 5.497\ \rm{mmol}\)
\(p = 122.5\ \rm{kPa} = 1.23 × 10^5\ \rm{Pa}\)
お疲れ様です!計算は大変でしたが,みなさん理解することはできましたか?計算に圧倒されることなく,この問題の本質を捉えてくださいね!




コメント