
今回は硫酸ナトリウムの溶解度曲線について解説していきます.
- 硫酸ナトリウムの溶解度曲線の特徴
- 解き方を徹底的にわかりやすく解説
を特にポイントとしています.昨日の自分より少しでもレベルアップしていきましょう!
解説してほしい分野があればぜひ次の記事のコメント欄で教えてくださいね!

硫酸ナトリウムの溶解度曲線ってなんで変な形しているの?
今回は硫酸ナトリウムの溶解度曲線について徹底解説していきます.みなさんもテキストや問題集などで解いたことがあるかもしれませんが,あんまりよく理解できていない…といった方も多いのではないでしょうか?この記事を読むことで,すべての疑問にお答えしていきます!
まずは,硫酸ナトリウムの溶解度曲線の概略図を示します.この図は問題集でよく見ていると思います.
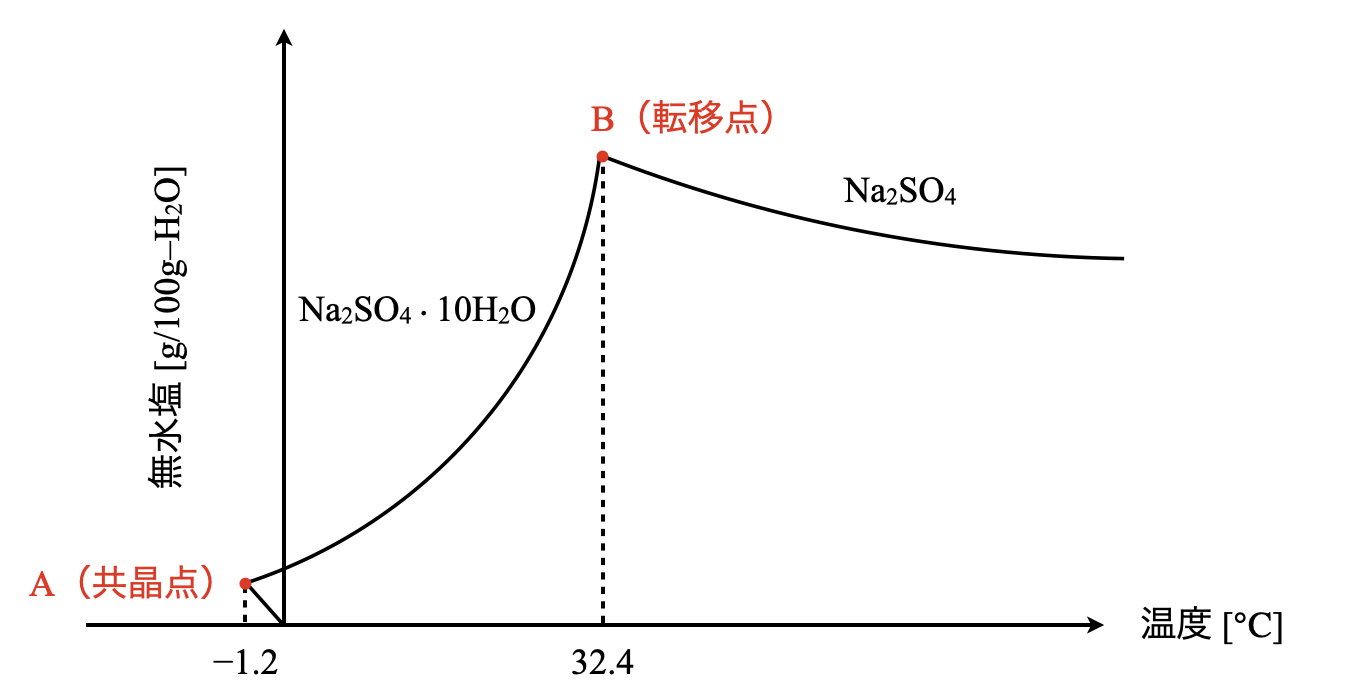
この溶解度曲線で他の物質とは違う点が\(2\)点あります.それは\(\rm{A}\)点と\(\rm{B}\)点です.\(\rm{A}\)点まで温度がマイナスとなり,そこから\(\rm{B}\)点に向けて温度が上昇していきます.しかしながら,\(\rm{B}\)点でカクッと折れまがり,今度は温度の上昇とともに溶解度が減少していきます.
ここで,\(\rm{A}\)点のことを共晶点,\(\rm{B}\)点のことを転移点といいます.
それぞれについて詳しく解説していきますね!
転移点
硫酸ナトリウムの溶解度曲線は,図のように\(\rm{32.4^\circ C}\)で折れ曲がっています.
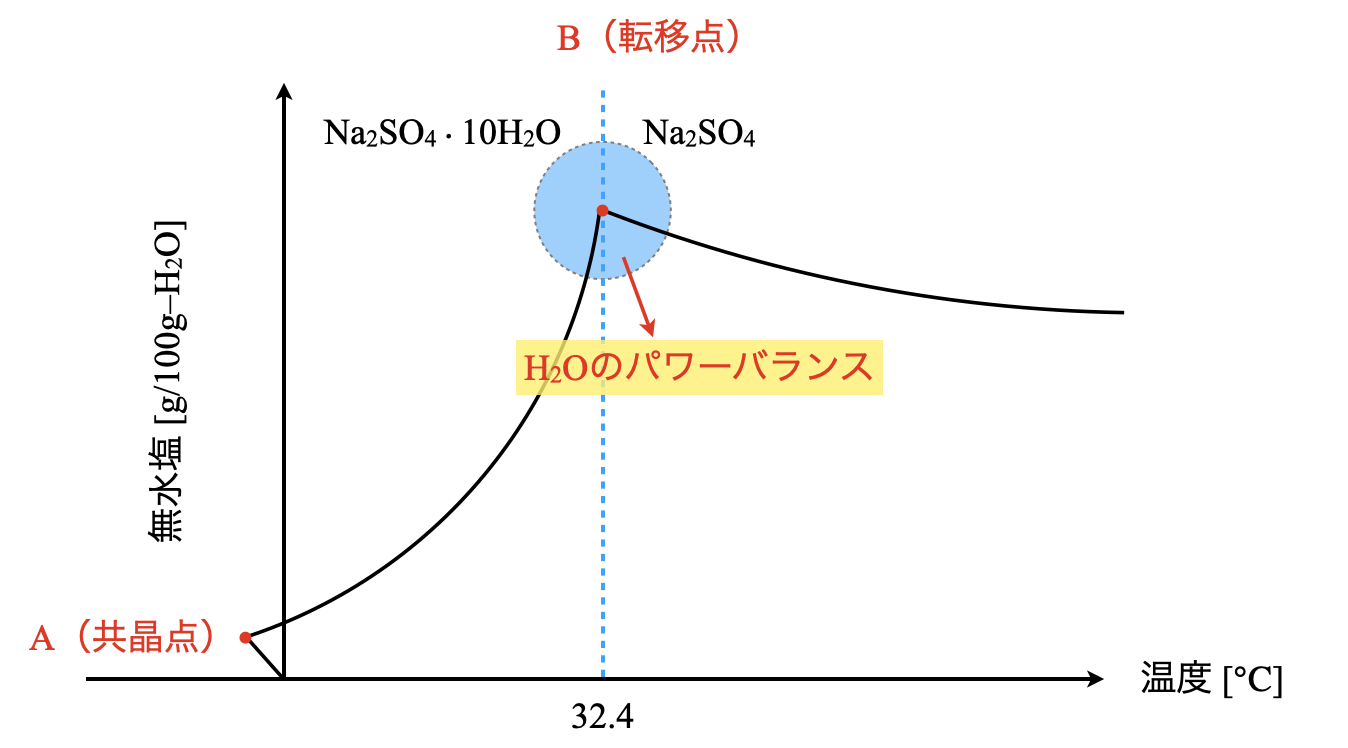
\(\rm{32.4^\circ C}\)より低い温度では\(10\)分子の水和水をもつ結晶\(\rm{Na_2SO_4 \cdot 10H_2O}\)が析出しますが,\(\rm{32.4^\circ C}\)より高い温度では水和水をもたない無水物\(\rm{Na_2SO_4}\)が析出します.このようにある温度・圧力を境として変化するとき,この点のことを転移点といいます.
この理由も解説しましょう!
これは高温では\(\rm{H_2O}\)分子の熱運動が激しくなり,\(\rm{Na_2SO_4}\)が\(\rm{H_2O}\)分子を結晶水として引き留めておくことが難しくなるためです.つまり,\(\rm{H_2O}\)分子のバランスによって転移点の左側か右側になるか決まるというわけです.ちょうど\(\rm{32.4^\circ C}\)では\(\rm{Na_2SO_4}\)と\(\rm{Na_2SO_4 \cdot 10H_2O}\)が共存できるため,両者が混ざり合って析出します.
共晶点
次に,共晶点について解説します.\(\rm{A}\)点の周りに関して,いつもの溶解度曲線とは逆に縦軸に温度,横軸に溶解度をとったグラフを書きます.
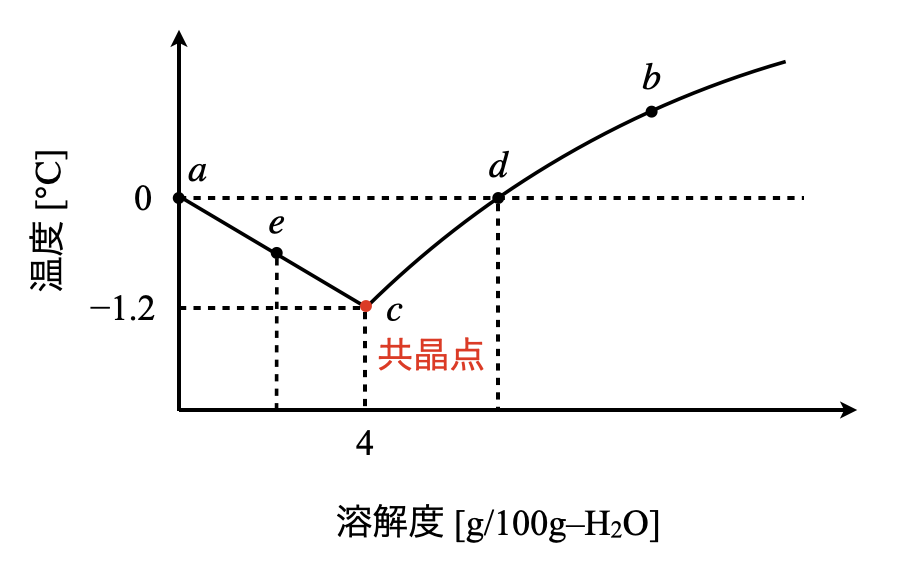
それぞれの曲線について詳しくみていきます.
- \(e\)点:溶液を冷却していくと,\(e\)点で氷を析出し始め,残液は次第に濃くなります.(水が少なくなるので,逆に濃度は高くなるわけです!)
- \(e→c:\)液温がさらに下がっていくと,凝固点が降下しながら\(c\)点となります.
- \(c\)点:この\(c\)点を共晶点といいます.\(c\)点に達すると,氷と同時に\(\rm{Na_2SO_4 \cdot 10H_2O}\)が析出します.このように凝固点降下が起こっていることがわかると思います.この点では溶液の濃度は変化しなくなるため,凝固点降下もこれ以上起こりません.そのため液温は一定となります.
- \(b→d:\)温度が下がると,\(\rm{Na_2SO_4 \cdot 10H_2O}\)の溶解度が少しずつ減少していきます.
- \(d→c:d\)点で\(\rm{Na_2SO_4 \cdot 10H_2O}\)を析出し始め,残液は次第に薄くなりながらやがて\(c\)点に到達します.
つまり,\(c\)点では氷と\(\rm{Na_2SO_4 \cdot 10H_2O}\)が一定の割合で析出します.このとき一定の割合とは,水\(\rm{100\ g}\)に\(\rm{Na_2SO_4\ 4\ g}\)の割合で凍ります.
上の解説を見ていただくとわかると思うのですが,共晶点には凝固点降下が深く関係しています.凝固点降下も記事にまとめていますので,そちらも見てみてください!

計算問題で実力アップ!
さて,硫酸ナトリウムの溶解度曲線を理解したところで,次は実際に問題を解いていきましょう.間違いやすいポイントなどをわかりやすく解説していきますよ!
硫酸ナトリウムの溶解度曲線を以下に示す.

\(\rm{60^\circ C}\)の硫酸ナトリウムの飽和水溶液\(\rm{100\ g}\)について考える.
(\(\rm{Na_2SO_4 = 142}\),\(\rm{H_2O = 18}\))
(\(1\))\(\rm{60^\circ C}\)に保ちながら水\(\rm{40\ g}\)を蒸発させたとき,析出する結晶は何\(\rm{g}\)?
(\(2\))\(\rm{20^\circ C}\)に冷却したら析出する結晶は何\(\rm{g}\)?
(\(3\))\(\rm{60^\circ C}\)に保ちながら水\(\rm{40\ g}\)を蒸発させた後,\(\rm{20^\circ C}\)に冷却したら合わせて何\(\rm{g}\)の結晶が析出するか?
まずは計算問題での硫酸ナトリウムの溶解度曲線の捉え方について解説します.一般的な溶解度曲線の問題と同じですよ!
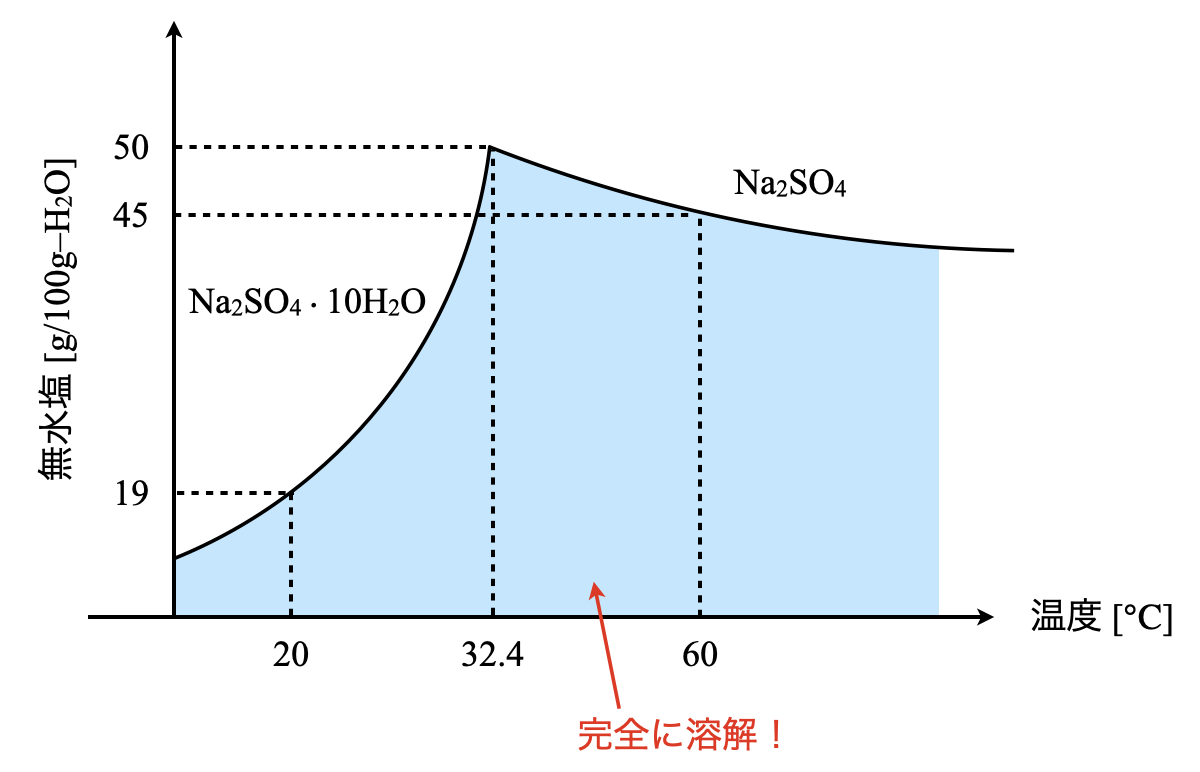
溶解度曲線より下の部分については完全に溶解し,それ以上溶質を溶かした場合については,一部が析出します.溶解度を考える上ではこの考え方は重要になりますので,イメージできるようにしておきましょう!
温度一定で蒸発
(\(1\))は温度を一定に保ったまま蒸発させる点がポイントです.\(\rm{60^\circ C}\)に保ちながら蒸発させるので,下の記事で解説したボックス図を使って解いていきます.

ここで最初に溶液に含まれていた溶質の質量を求めて,結晶が何\(\rm{g}\)析出したのかといった正統派で求めてももちろん大丈夫です.一応下に示しておきます.ただこのやり方を見ていただくとわかると思いますが,計算量が多すぎます……
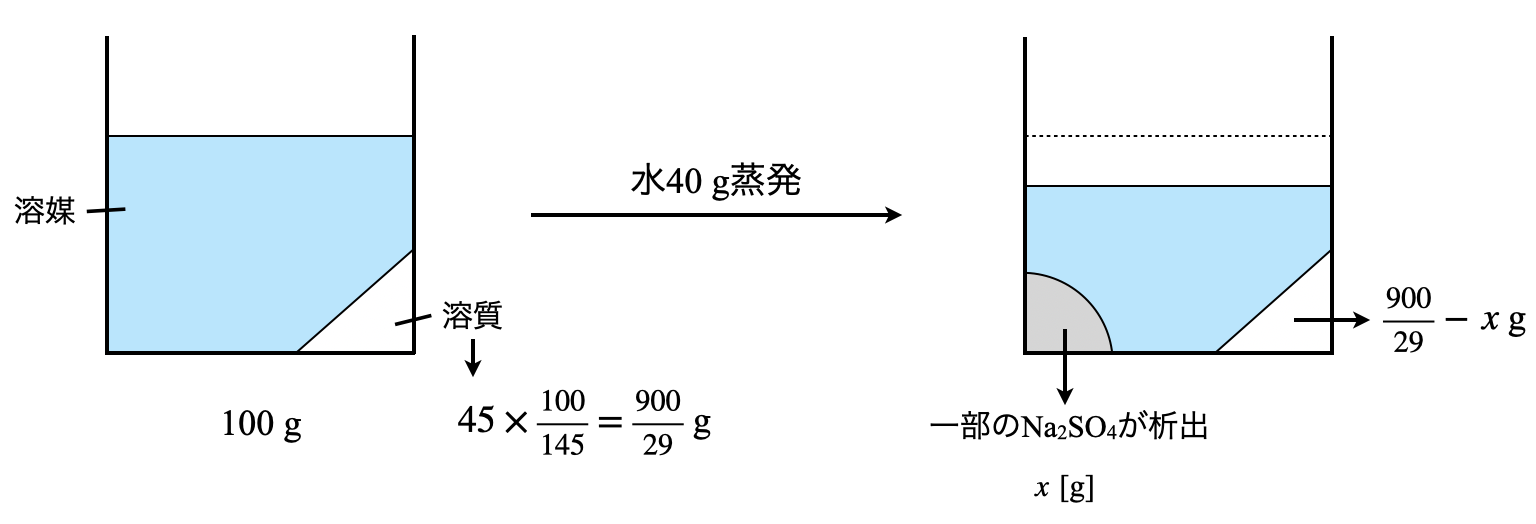
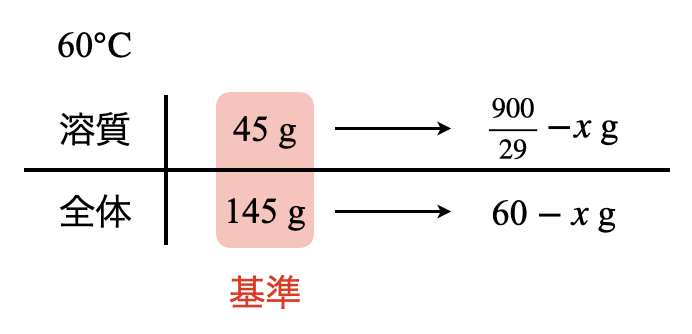
そしてこのボックス図から以下のような式を導くことができます.
\(\large \frac{45}{145} \small = \large \frac{\frac{900}{29}\ -\ x}{60\ -\ x}\)
ただこのやり方を見ていただくとわかると思いますが,計算量が多すぎます……
問題文に「\(\rm{60^\circ C}\)に保ちながら水を\(\rm{40\ g}\)蒸発させると,\(\rm{Na_2SO_4}\)の結晶が析出する」とあります.これをそのまま考えると大変なので,言い換えましょう!
「水\(\rm{40\ g}\)に溶解していた\(\rm{Na_2SO_4}\)が水がなくなったことで溶解できなくなり析出する」と考えることができます.
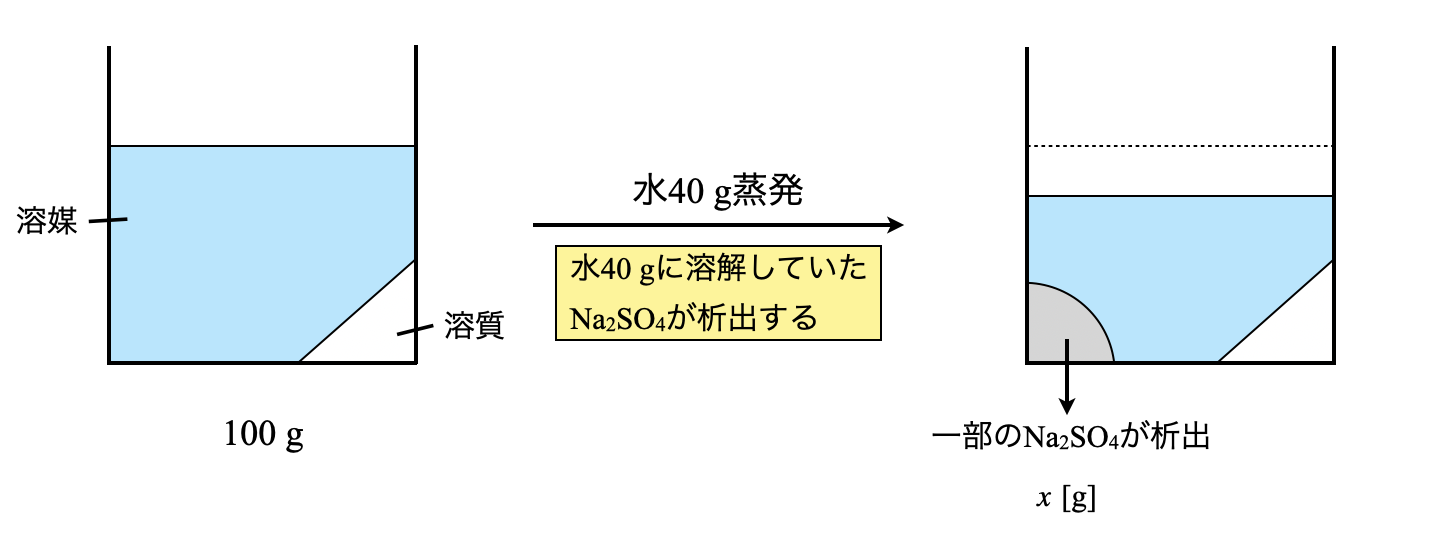
このとき析出する\(\rm{Na_2SO_4}\)を\(x\ \rm{[g]}\)とすると,以下のようなボックス図を考えることができます.
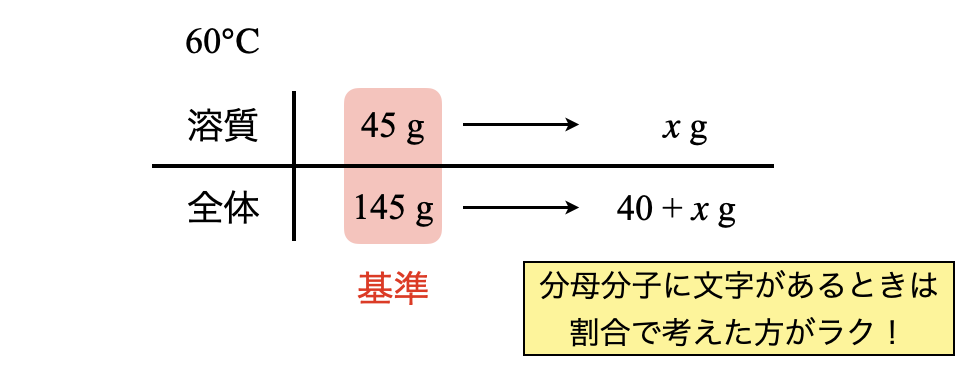
このとき,分母分子に文字が含まれているので,割合で考えていきましょう.
\(\large \frac{45}{145} \small = \large \frac{x}{40\ +\ x}\)
これを解くと,\(x = 18\ \rm{g}\)となり,簡単に求めることができましたね!
今回の問題が溶解度曲線の中でどのような動きをしたのかを確認しておきましょう.ボックス図とともに溶解度曲線も自在に使いこなせるようになると最強になりますよ!
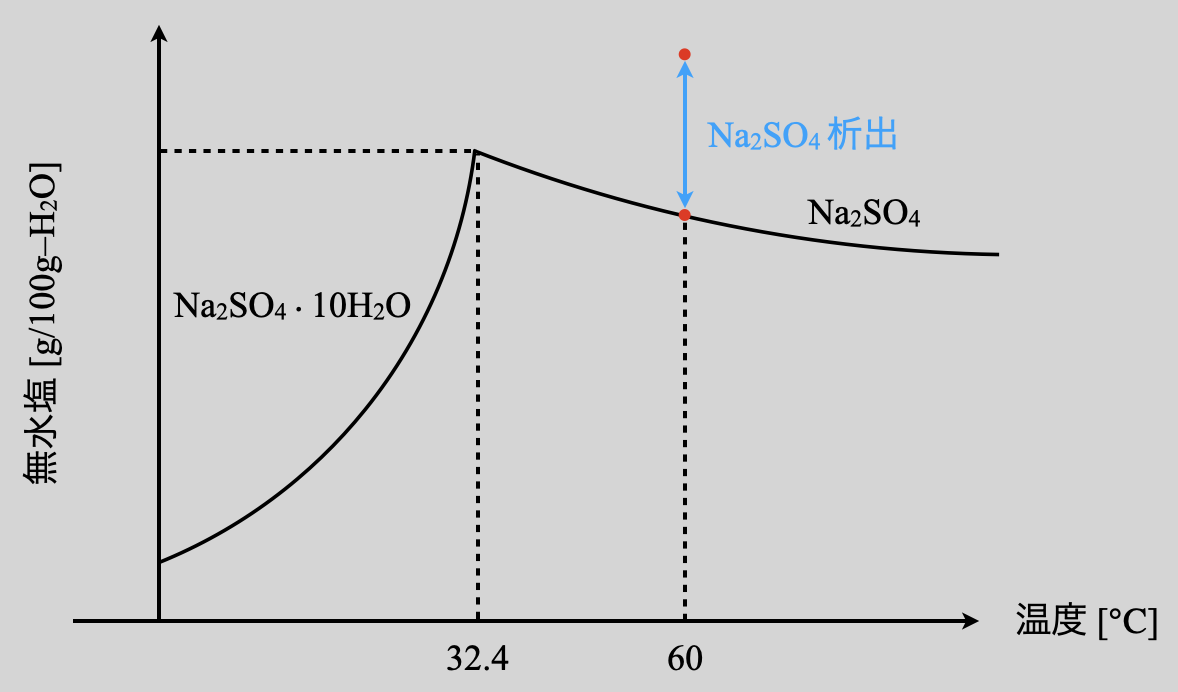
今回の問題では,\(\rm{60^\circ C}\)で温度一定として,水を一部蒸発させています.最初はちょうど飽和溶液だったので,曲線上に点が存在していることになります.そこから水が減ると,溶解できる量は減少していくので,相対的に点は上に上がっていくことになります.そして曲線より上に超えた部分の量が,析出する質量となります.
冷却
(\(2\))は温度を気にせず,一気に冷却させていきます.ボックス図を書くためには,溶質と全体の情報が必要なので,まず\(\rm{60^\circ C}\)での溶質の質量を求めていきます.
ステップ\(1:\)溶質の質量を求める
この\(\rm{60^\circ C}\)の溶液は飽和しているので,ボックス図で簡単に溶質を求めることができます.
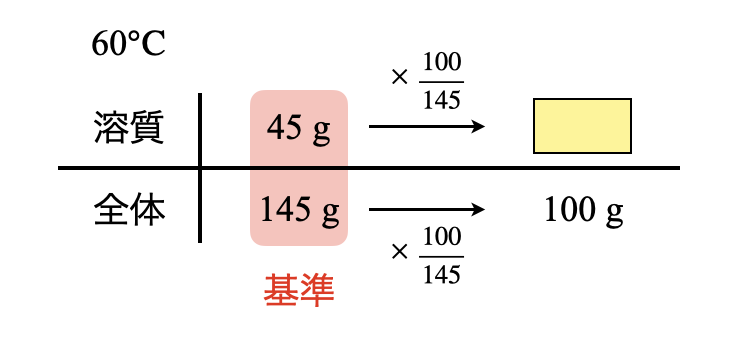
溶質\(:45 × \large \frac{100}{145} \small = 31\ \rm{g}\)
ステップ\(2:\)溶液の温度を\(\rm{20^\circ C}\)にして冷却する
溶質の質量がわかったところで,\(\rm{20^\circ C}\)に冷却していきます.\(\rm{20^\circ C}\)での溶解度を見ると,\(19\)であることがわかります.そしてこのとき析出するのは,\(\rm{Na_2SO_4 \cdot 10H_2O}\)になります.この質量を\(y\ \rm{[g]}\)とすると,溶質は分子量から\(\large \frac{142}{322} \small y\ \rm{[g]}\)であるとわかります.
すると,\(\rm{20^\circ C}\)でのボックス図を次のように書くことができます.
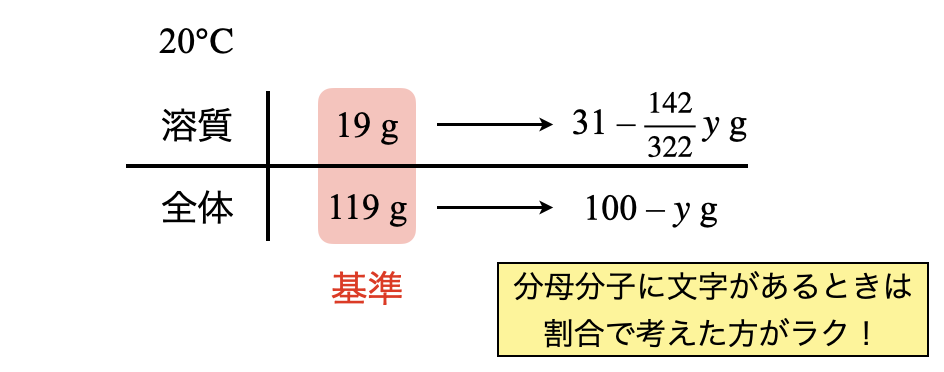
これは分母分子に文字が含まれているので,割合で計算していきましょう!
\(\large \frac{19}{100\ +\ 19} \small = \large \frac{31\ -\ \frac{142}{322}y}{100\ -\ y}\)
これを解くと,\(y = 53.4\ \rm{g}\)となります.
(\(2\))についても溶解度曲線上での動きを確認しておきましょう!
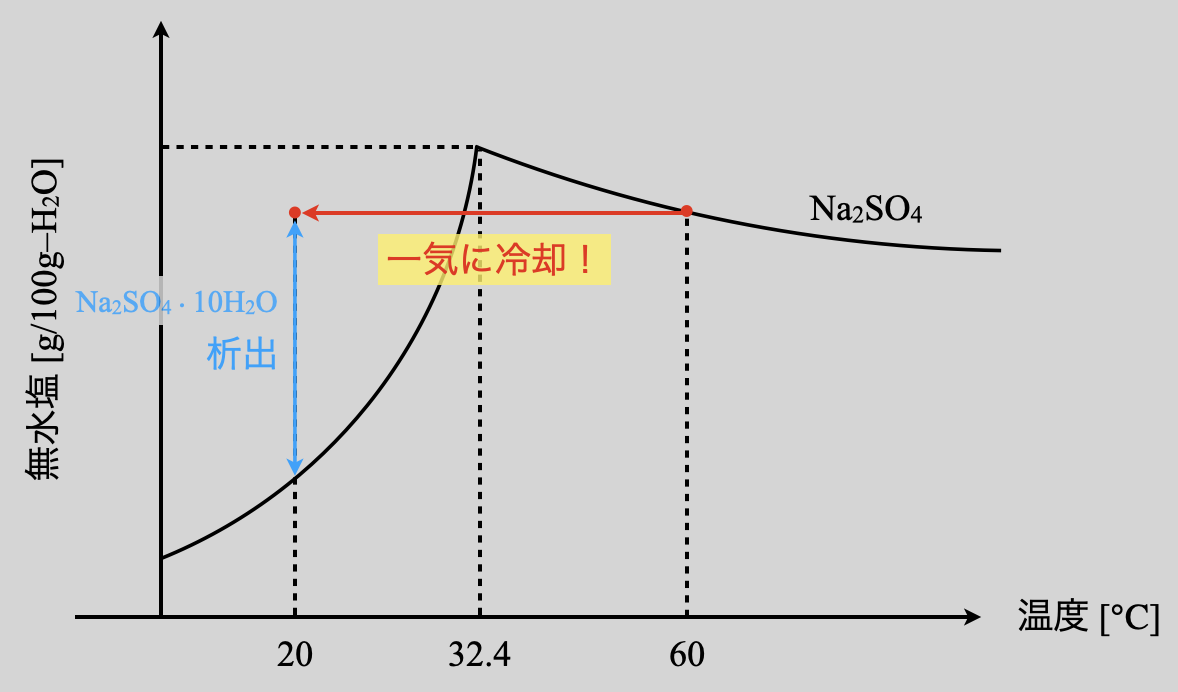
\(\rm{60^\circ C→20^\circ C}\)に一気に冷却しているので,横一直線に線を引きます.そして\(\rm{20^\circ C}\)での溶解度曲線との間の質量が析出することになります.ここでポイントが\(1\)つあります.
それは,\(\rm{32.4^\circ C}\)(\(\rm{Na_2SO_4}\)と\(\rm{Na_2SO_4 \cdot 10H_2O}\)の境目の温度)を通過するとき,その頂点よりも直線が下にあるということです.
そのため,今回の問題では\(\rm{Na_2SO_4}\)は析出しません.この違いが(\(3\))で明らかになります.最後まで読んだ後に,ここに戻ってそれぞれの問題の違いを理解してみてくださいね!
温度一定で蒸発→冷却
(\(3\))は\(\rm{60^\circ C}\)で一定に保ちながら水を蒸発させ,その後冷却しています.この問題は複雑なので,\(3\)つのステップに分けて考えていきましょう!
ステップ\(\rm{1:60^\circ C}\)で一定に保ちながら水を蒸発させる
\(\rm{60^\circ C}\)で一定に保ちながら水を\(\rm{40\ g}\)蒸発させる操作は,(\(1\))と全く同じ問題です.そのため,\(\rm{18\ g}\)の\(\rm{Na_2SO_4}\)が析出することがわかります.
ステップ\(\rm{2:32.4^\circ C}\)での析出量を考える
次に,\(\rm{60^\circ C→32.4^\circ C}\)に温度を下げていくと,溶解度は上昇していきます.そのため,一度析出した\(\rm{Na_2SO_4}\)がどんどん溶解していきます.そして,\(\rm{32.4^\circ C}\)のときに析出する\(\rm{Na_2SO_4}\)の質量を\(x\ \rm{[g]}\)として求めていきます.このとき,ボックス図は以下のようになります.
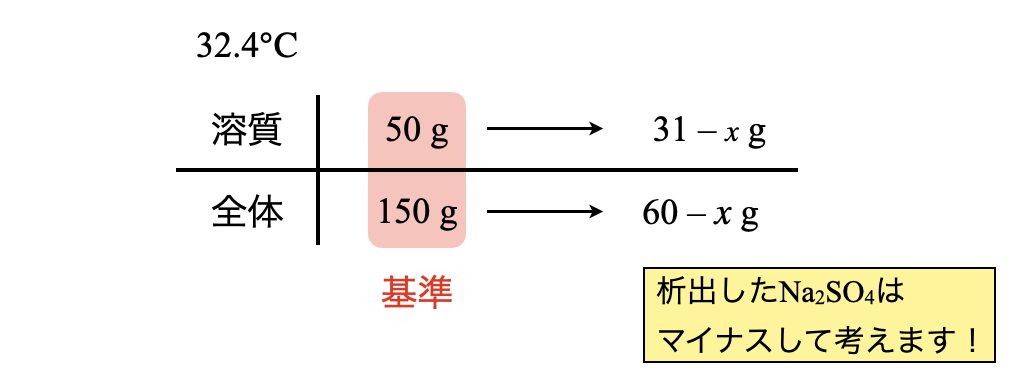
分母分子に文字が含まれているので,ここでも割合で考えていきます.
\(\large \frac{50}{150} \small = \large \frac{31\ -\ x}{100\ -\ 40\ -\ x}\)
これを解くと,\(x = 16.5\ \rm{g}\)となります.つまり,\(\rm{32.4^\circ C}\)において\(\rm{Na_2SO_4}\)が\(\rm{16.5\ g}\)析出することになります.
ステップ\(\rm{3:20^\circ C}\)での析出量を考える
次に溶液を\(\rm{20^\circ C}\)に下げていきます.先ほどのステップで\(\rm{Na_2SO_4}\)が一部析出しているので,この溶液は飽和溶液となっています.つまり,\(\rm{32.4\circ C}\)のとがった点から冷却していくといったイメージになります.
そして\(\rm{32.4^\circ C→20^\circ C}\)に温度下げていくと,今度は\(\rm{Na_2SO_4 \cdot 10H_2O}\)が析出していきます.このとき析出する\(\rm{Na_2SO_4 \cdot 10H_2O}\)を\(y\ \rm{[g]}\)とします.
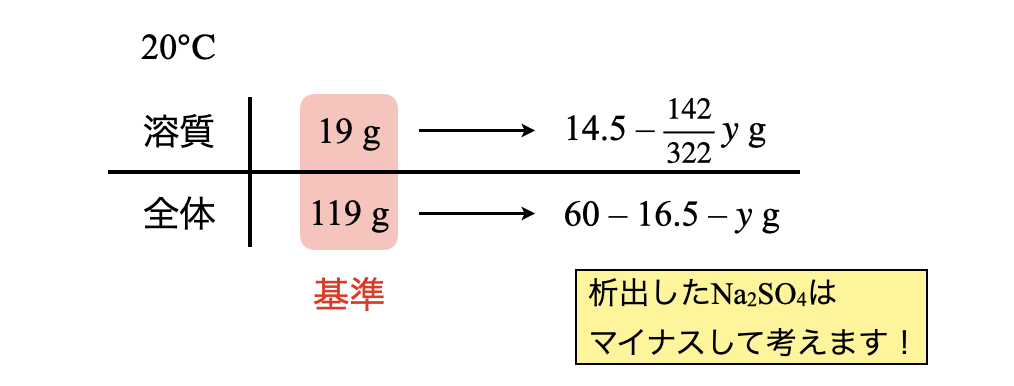
\(\large \frac{19}{119} \small = \large \frac{14.5\ -\ \frac{142}{322}y}{43.5\ -\ y}\)
これを解くには時間がかかりますが,ここのテクニックは申し訳ないですがありません…
これを解くと,\(y = 26.9\ \rm{g}\)となります.
よって,析出するのは,\(\rm{Na_2SO_4}\)と\(\rm{Na_2SO_4 \cdot 10H_2O}\)を合わせた量となり,
\(\rm{16.5 + 26.9 = 43.4\ g}\)
となります.
(\(3\))について溶解度曲線上での動きを確認しておきましょう!
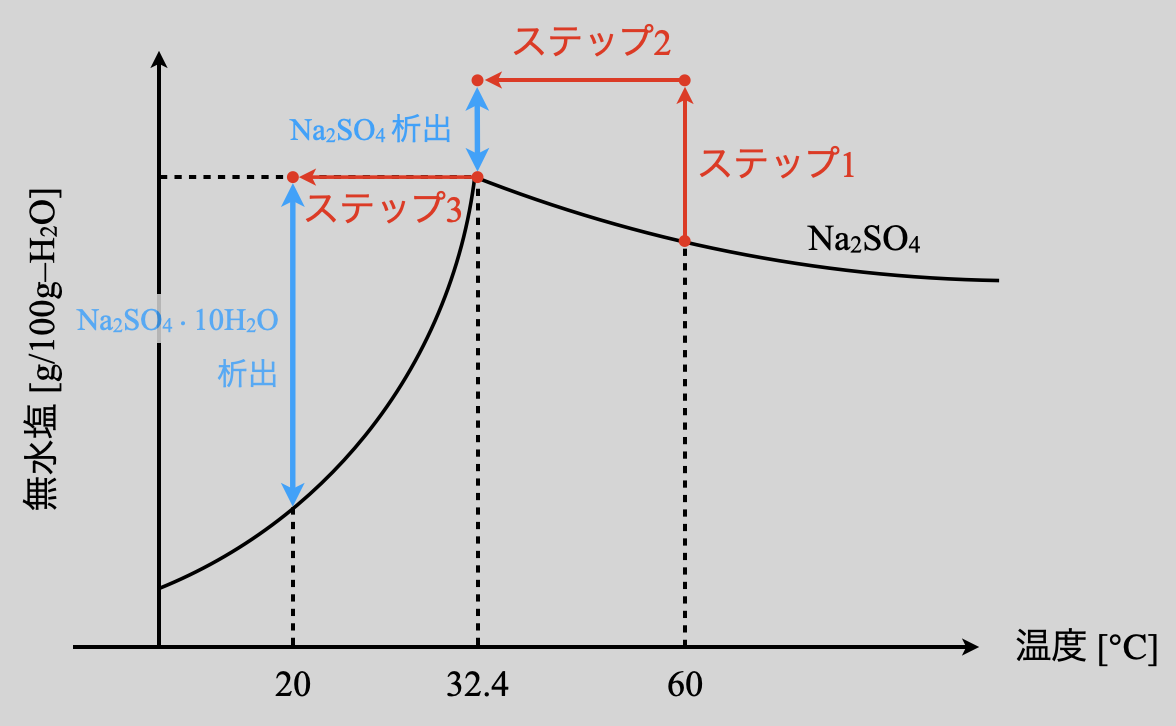
まずは\(\rm{60^\circ C}\)上において水を蒸発しているので,溶解度が下がり析出する\(\rm{Na_2SO_4}\)が多くなります.これは(\(1\))と全く同じです.そして\(\rm{60^\circ C→32.4^\circ C}\)に冷却していきます.ここで(\(2\))との違いは,\(\rm{32.4^\circ C}\)のとき溶解度曲線と交わっていないという点です.つまり,\(\rm{32.4^\circ C}\)のときに一部\(\rm{Na_2SO_4}\)が析出します.
そして次に,\(\rm{32.4^\circ C→20^\circ C}\)にさらに冷却していきます.ここの始点が\(2\)つの溶解度曲線の交点になることに気をつけてくださいね!これは\(\rm{Na_2SO_4}\)が一部析出して再び飽和溶液となるためです.
\(\rm{32.4^\circ C}\)において溶解度曲線と交わるかどうかで解き方が根本的に変化してくる!ということをしっかりと覚えていてくださいね!



コメント