
ヘスの法則とエネルギー図を使うと,簡単に反応熱を求めることができます!
それでは,今日も頑張っていきましょう!!
解説してほしい分野があればぜひ次の記事のコメント欄で教えてくださいね!

\(\rm{You Tube}\)ではより具体的な問題を解説しているので,ぜひそちらもご覧ください!
Hessの法則
それでは,まず\(\rm{Hess}\)の法則(ヘスの法則)を解説していきましょう!
ちなみに,\(\rm{Hess}\)は\(1840\)年スイス生まれのロシアのおじさんです!
\(\rm{Hess}\)の法則とは,
「反応熱は,反応の最初と最後の状態だけで決まり,反応の経路や方法には無関係である.」
というものです.
わかりやすく考えていきましょう!
\(\rm{A\ →\ B}\)に物質を変化させるために,以下の\(2\)つの工程があるとします.

ここで,\(\rm{A\ →\ C}\)に変化するときに発生する熱が\(Q_{\rm{AC}}\ \rm{kJ}\),\(\rm{C\ →\ B}\)に変化するときに発生する熱が\(Q_{\rm{CB}}\ \rm{kJ}\)とします.すると,\(\rm{A\ →\ C\ →\ B}\)に変化するときの全体的な熱は\(Q\ =\ Q_{\rm{AC}}\ +\ Q_{\rm{CB}}\)となります.
次に,\(\rm{A\ →\ D}\)に変化するときに発生する熱が\(Q_{\rm{AD}}\ \rm{kJ}\),\(\rm{D\ →\ B}\)に変化するときに発生する熱が\(Q_{\rm{DB}}\ \rm{kJ}\)とします.すると,\(\rm{A\ →\ D\ →\ B}\)に変化するときの全体的な熱は\(Q^{’}\ =\ Q_{\rm{AD}}\ +\ Q_{\rm{DB}}\)となります.
ここで,反応の全体を見ると,どちらも\(\rm{A\ →\ B}\)に変化しているので,\(Q\ =\ Q^{’}\)となるはずです.
このようにエネルギーが経路によらないという法則のことを\(\rm{Hess}\)の法則といいます.
これはエネルギー図を使って考えると,とてもわかりやすくなります.
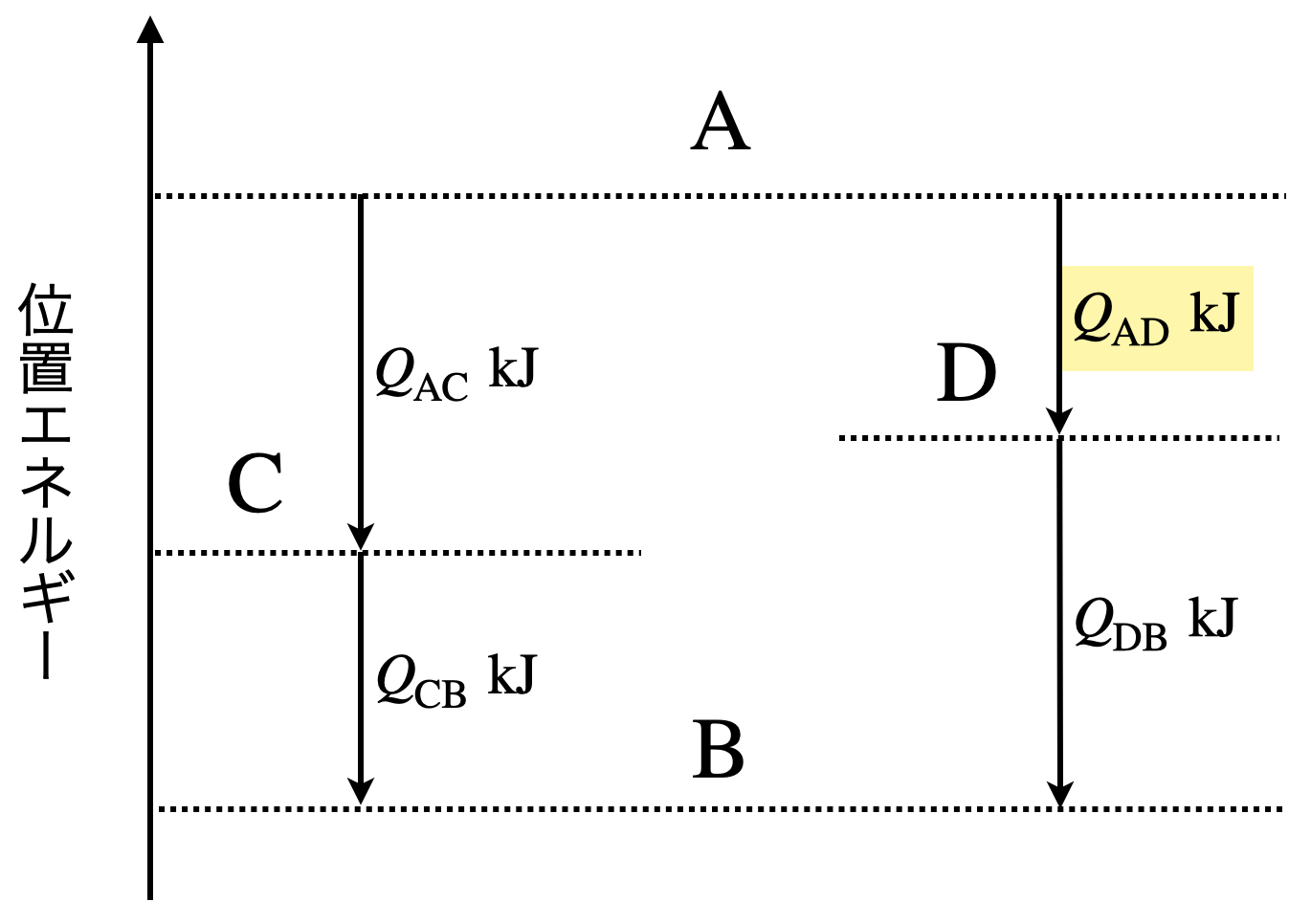
この図の中で,\(Q_{\rm{AD}}\)がわからないというときは,以下の式から求めることができます.
\(Q_{\rm{AC}}\ +\ Q_{\rm{CB}}\ =\ Q_{\rm{AD}}\ +\ Q_{\rm{DB}}\)
実際に問題を解きながら考えていきましょう.
\(\rm{C}\)の燃焼熱:\(394\ \rm{kJ/mol,CO}\)の燃焼熱:\(283\ \rm{kJ/mol}\)である.
\(\rm{CO}\)の生成熱は?
それぞれの解き方について順に解説していきましょう!
【解法1:熱化学方程式で解く】
それではまず,熱化学方程式で解く方法です.
与えられている反応熱から熱化学方程式を書いていきましょう.
\(\rm{C}\)の燃焼熱:\(\rm{C(s)\ +\ O_2(g)\ =\ CO_2(g)\ +\ 394\ kJ}\)
\(\rm{CO}\)の燃焼熱:\(\rm{CO(g)\ +\ \large \frac{1}{2} \small O_2(g)\ =\ CO_2(g)\ +\ 283\ kJ}\)
次に求めるべき反応熱の熱化学方程式を書いていきます.
\(\rm{CO}\)の生成熱:\(\rm{C(s)\ +\ \large \frac{1}{2} \small O_2(g)\ =\ CO(g)\ +\ }\)\(Q\ \rm{kJ}\)
上の最初の\(2\)式を変形することで,求めるべき熱化学方程式にしていきます.
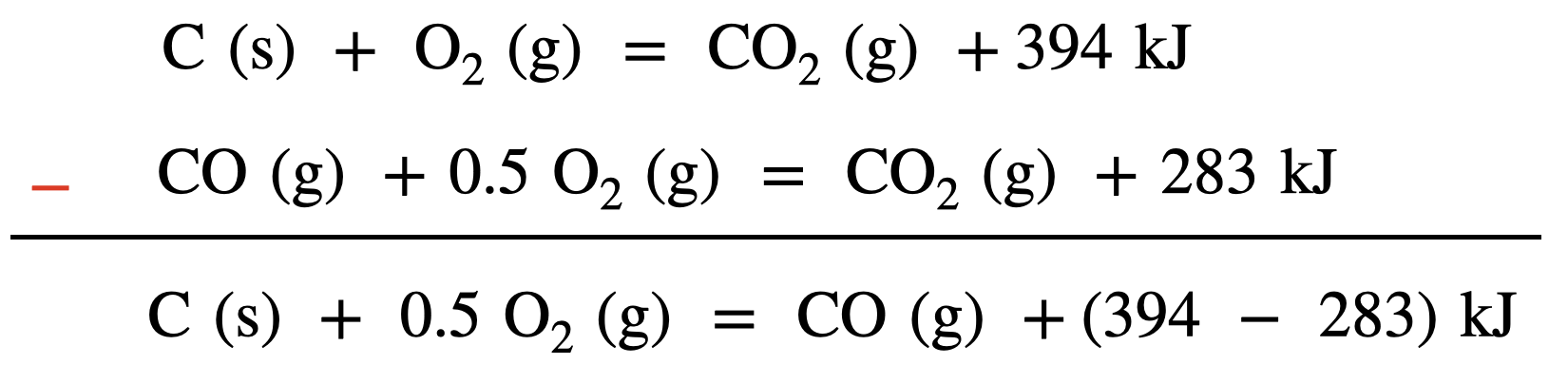
ここで,「\(-\)」の場合は反対側に書きます!
すると,\(\rm{CO}\)の生成熱は\(\ 111\ \rm{kJ/mol}\)であることがわかります!
【解法2:エネルギー図で解く】
先程の解法では,多くの物質が与えられると,熱化学方程式が多くなり,非常に複雑になります.そのため,エネルギー図を使って解く方法を説明していきます.
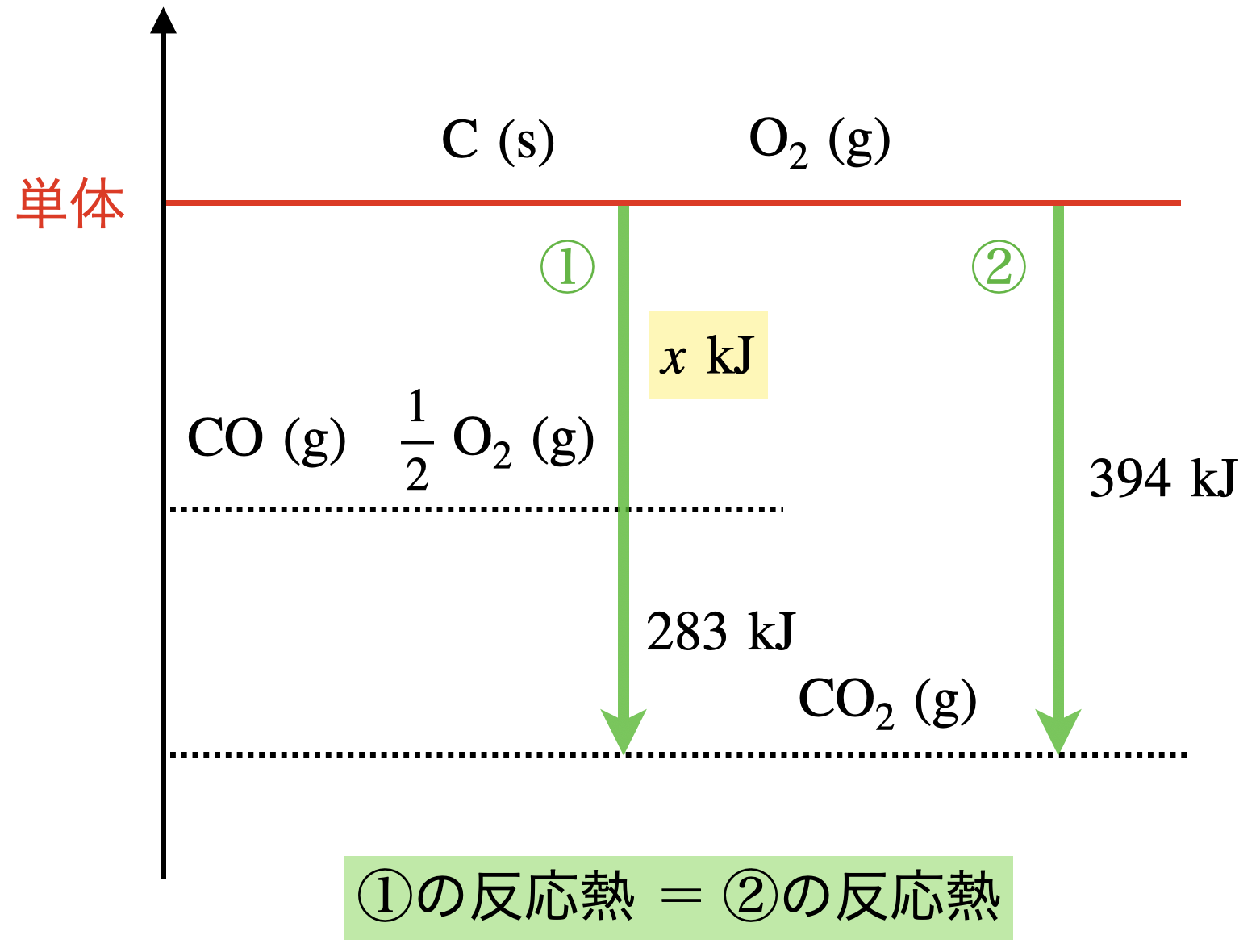
現在の状態をエネルギー図で表すと,下のようになります.

これを単純に引き算するだけで,\(Q\ =\ 394\ -\ 283\ =\ 111\ \rm{kJ/mol}\)とわかります.
こちらの方が簡単で速く解けます!
そのため,エネルギー図での解き方を是非マスターしてほしいです!
このように\(\rm{Hess}\)の法則では,与えられていない反応熱を足したり引いたりすることで,求めることができるという法則です.
先程のエネルギー図で考えると,①と②では反応経路が異なりますが,最終的な「単体 → 完全燃焼」で得られる熱は\(394\ \rm{kJ}\)となります.そのため足し算や引き算をすることで,与えられていない熱を求めることができるのです!
エネルギー図の基礎を完全マスター
この分野は練習が一番なので,どんどん練習していきましょう!
次の生成熱が与えられている.
\(\rm{C_2H_4:-52\ kJ/mol,C_2H_6:85\ kJ/mol,CO_2:394\ kJ/mol}\)
以下の反応熱\(Q_1,Q_2\ \rm{kJ/mol}\)を求めよ.
(\(1\))\(\rm{C_2H_4(g)\ +\ H_2(g)\ =\ C_2H_6(g)\ +\ }\)\(Q_1\ \rm{kJ}\)
(\(2\))\(\rm{C_2H_4(g)\ +\ 3O_2(g)\ =\ 2CO_2(g)\ +\ 2H_2O(l)\ +\ }\)\(Q_2\ \rm{kJ}\)
(\(1\))
それではエネルギー図を書いて考えていきましょう!

①生成熱が「\(-\)」の場合でもプラスと同じように書く.
②単体の生成熱は\(0\ \rm{kJ/mol}\)となる.
これは,\(\rm{H_2(g)\ =\ H_2(g)\ +\ 0\ kJ}\)ということです!
この\(2\)点をしっかりと覚えてください!
すると,\(Q_1\)が簡単に求められます.
\(Q_1\ =\ 85\ -\ (-52)\ =\ 137\ \rm{kJ/mol}\)
(\(2\))
先程のポイント通りに書くと,下のようなエネルギー図になります.
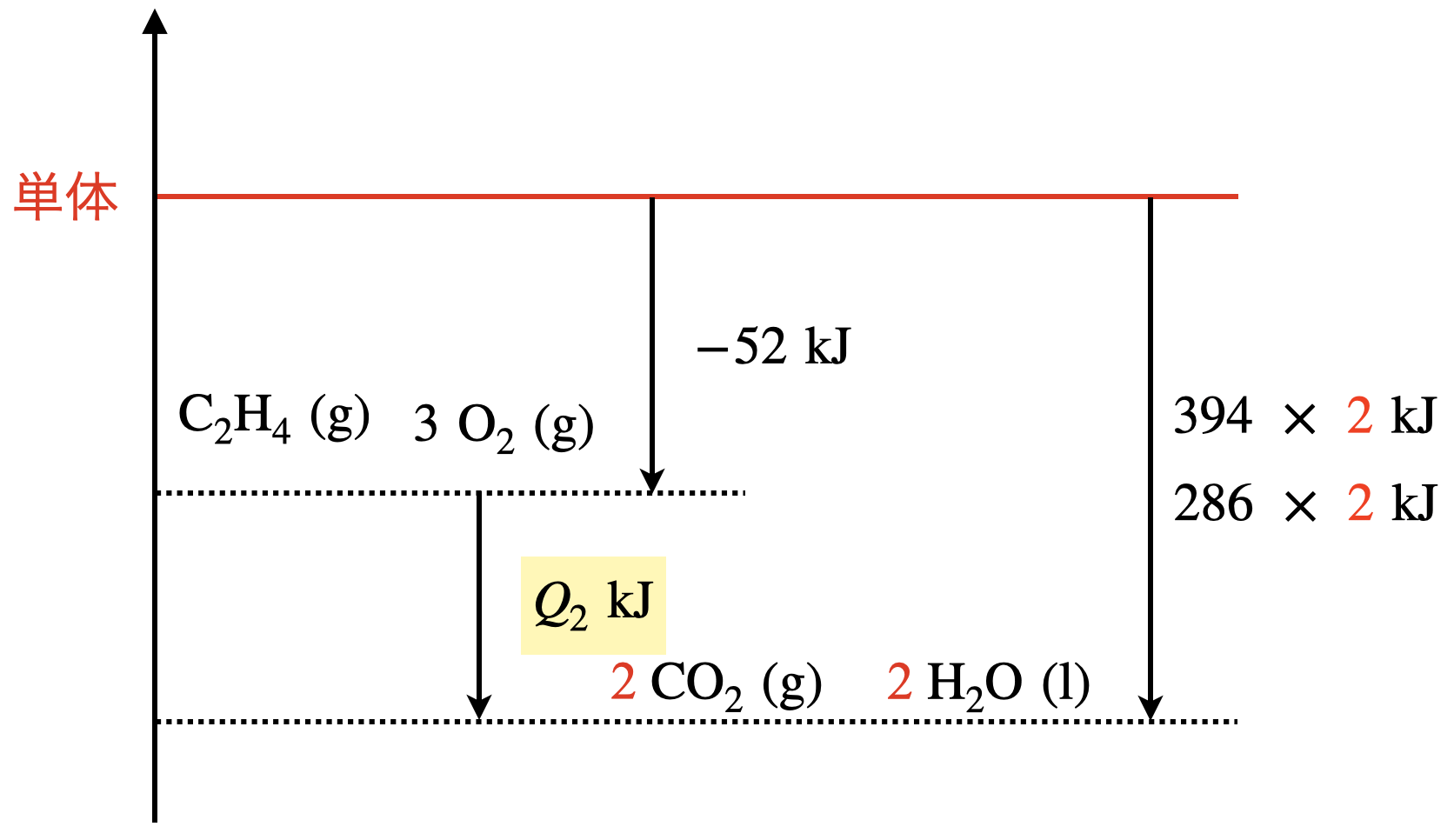
考える物質が\(2\ \rm{mol}\)の場合は,\(2\)倍の生成熱を考えます.そのため,図では\(2\)倍にしています!
これから
\(Q_2\ =\ (394\ +\ 286)\ ×\ 2\ -\ (-52)\ =\ 1412\ \rm{kJ/mol}\)
となります.
つまり熱のデータについて最も大切なのは生成熱なのです.
それでは次の問題を解いていきましょう!
次の生成熱が与えられている.
\(\rm{KOH_{(s)}:425\ kJ/mol,HNO_{3(l)}:174\ kJ/mol,KNO_{3(s)}:493\ kJ/mol,H_2O_{(l)}:286\ kJ/mol}\)
また,次の溶解熱が与えられている.
\(\rm{KOH_{(s)}:58\ kJ/mol,HNO_{3(l)}:33\ kJ/mol,KNO_{3(s)}:-35\ kJ/mol,H_2O_{(l)}:0\ kJ/mol}\)
この場合,以下の\(Q\)を求めよ.
\(\rm{KOH_{aq}\ +\ HNO_{3aq}\ =\ KNO_{3aq}\ +\ H_2O_{(l)}\ +\ }\)\(Q\)
今回の問題では,ある固体の物質を溶媒に溶解することで,溶解熱というものが発生します.そのため生成熱だけではなく,溶解熱も考慮する必要があります.
前回の記事でも説明しましたが,溶解熱はプラスにもマイナスにもなるため,これも考慮したエネルギー図を書くと複雑になります.そのため,以下のような図を書くとわかりやすくなります!

このようにすると,反応全体では下のようなエネルギー図になります.
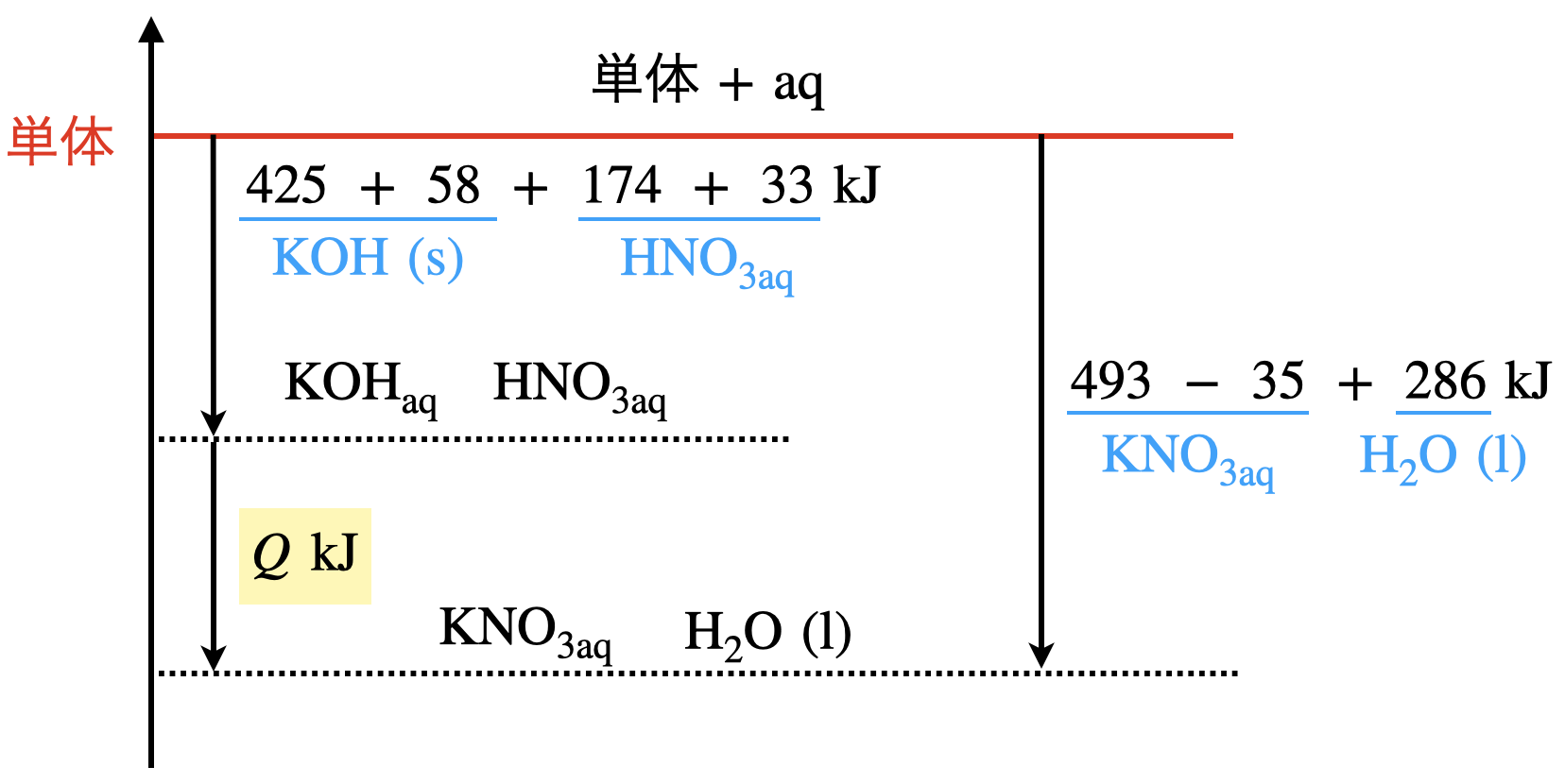
この図から\(Q\ =\ 54\ \rm{kJ/mol}\)となります.
本日はここまでです,お疲れ様です!
今回は生成熱や燃焼熱,溶解熱を具体例を使って解説していきました!
1回では理解しきれないところは何度も読み直して必ず解けるようにしてくださいね!
それでは,次回は結合エネルギーやイオン化エネルギーを使った問題を解説していきます!
入試問題などを解くと,素早く解けることを実感できます!



コメント