[H+]計算を完全マスター！③

前回までで強酸や1価の弱酸の[H+]計算について学んできました！
今日は最後の2価の弱酸について詳しく説明していきます！

このシリーズも今日で最後なので，しっかりと頑張っていきましょう！！
強酸や1価の弱酸についてまだ読んでいない方は，是非こちらもご一読ください！
[H+]計算を完全マスター！①
[H+]計算を完全マスター！②

弱酸（2価）

弱酸（2価）・（近似解）

2価の弱酸というのは，2回電離するということです．
詳しいことは下の問題で見ていきますが，2価になると化学平衡が2回起きるようになります．
ということは，平衡定数も2個出てくるというわけです！

このような問題は，難関大などで頻出ですが，しっかりと解説していきますので，大丈夫ですよ！！

それでは，2価の弱酸の近似解の場合について考えていきます．

まずは，\(\rm{H_2S}\)の2段階電離を考えてみましょう！

H₂S　⇄　HS^–　+　H⁺
HS^–　⇄　S^2-　+　H⁺

2段階電離のときは，各電離の起こりやすさを比較してみることが大切です！

\(K_{\rm{a1}} = 1.0 × 10^{-7}\ \rm{mol/L}\)で\(K_{\rm{a2}} = 1.0 × 10^{-13}\ \rm{mol/L}\)ということは，
第1電離の方が\(1.0 × 10^6\)倍起こりやすいということです！

つまり，第2電離は考えなくていいということです！
ここが非常に大切で，ほとんどの場合，第2電離は無視することができます！

第2電離を無視すると，次のようになります！

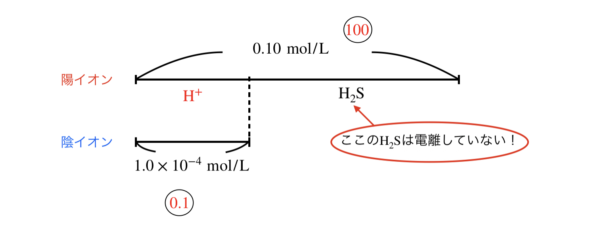
\([\rm{H}^+]\)を近似解で求めると，
\([\rm{H}^+] = \sqrt{0.1 × 1.0 × 10^{-7}} = 1.0 × 10^{-4}\ \rm{mol/L}\)
となります！

いつものように，最後の確認までしてくださいね！
全体：\([\rm{H}^+] = 0.1：1.0 × 10^{-4} ＝ 100：0.1\)
これより，近似解を使うのはOKですね！！

弱酸（2価）・（厳密解）

いよいよ，最後のパターンになりました！
次は2段階電離する弱酸で近似解が使えないバージョンです！

少し難しいですが，あともう少しです！
頑張りましょう！！

炭酸の2段階電離は次のようになります！

CO₂　+　H₂O　⇄　HCO₃^–　+　H⁺
HCO₃^–　⇄　CO₃^2-　+　H⁺

ここで，注意点があります．

さて，再び各電離の起こりやすさを比較してみましょう！
\(K_{\rm{a1}} = 5.0 × 10^{-7}\ \rm{mol/L}\)で\(K_{\rm{a2}} ＝ 5.0 × 10^{-11}\ \rm{mol/L}\)ということは，
第1電離の方が\(1.0 × 10^4\)倍起こりやすいということです！

つまり，第2電離は考えなくていいということです！

そうすると，図は次のようになります！

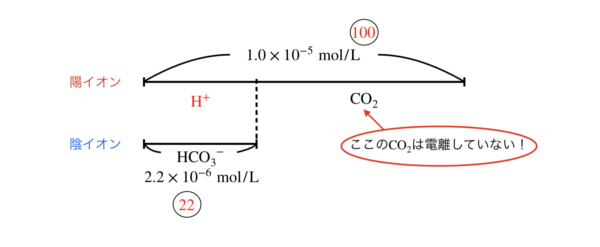
\([\rm{H}^+]\)を近似解で求めると，
\([\rm{H}^+] = \sqrt{1.0 × 10^{-5} × 5.0 × 10^{-7}}=2.2 × 10^{-6}\ \rm{mol/L}\)
となります！

ここで終わってはいけませんよ！
全体：\([\rm{H}^+]\)の比を考えてみましょう！

全体：\([\rm{H}^+] = 1.0 × 10^{-5}：2.2 × 10^{-6} ＝ 100：22\)
これは\(100：5\)以上となるので，近似解を使ってはいけません！！！
ここが先ほどの問題と違うところです！

近似解を用いない方法は以前学習しましたね！？
図にすると下のようになります．

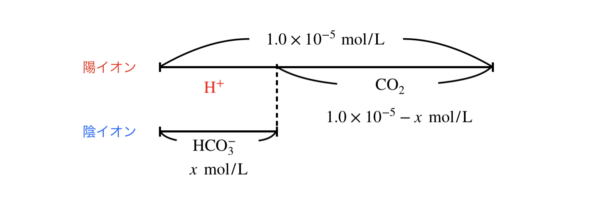
ただし，\(K_{\rm{a1}} >> K_{\rm{a2}}\)となるので，第1電離の方のみ考えればいいのは変わりませんよ！
\([\rm{H}^+] = [\rm{HCO3}^-] = \)\(x\ \rm{mol/L}\)，\([\rm{CO_2}] = \)\(1.0 × 10^{-5} – x\ \rm{mol/L}\)を\(K_{\rm{a1}}\)の式に代入すると，

\(K_{\rm{a1}} = \large \frac{x \cdot x}{1.0 × 10^{-5} -x} \normalsize = 5.0 × 10^{-7}\)

\(x^2 + 5.0 × 10^{-7} x – 5.0 × 10^{-12} = 0 \)

これは因数分解できます！

\((x – 2.0 × 10^{-6})(x + 2.5 × 10^{-6}) = 0\)

\(x = [\rm{H}^+] = 2.0 × 10^{-6}\ \rm{mol/L}\)
となります！

今回で酸の電離については，全てのパターンを学習しました！
あとは，何度も復習して確実に解けるようにしてくださいね！！

今回はお疲れ様でした！