今回のメニューです!
✅「イオン化エネルギー」と「電子親和力」の違い
✅イオン化エネルギーの大小関係
この記事を読むことで、イオン化エネルギーの考え方をしっかりと理解できます。
理論化学の中での原子の構造のポジションを確認しておきましょう。
原子の構造は、「物質の構造」の中の「イオン化エネルギー」に関する項目です。
「原子半径」を基礎として考えることで、イオン化エネルギーの理解が深まるので、原子半径の分野もしっかり理解しておきましょう。

イオン化エネルギーと電子親和力の関係
原子半径は原子核に存在する陽子と電子の引力に基づいて決まる値でした。
そのため、原子半径の考え方を応用すると、イオン化エネルギーや電子親和力を簡単に理解することができます。
・イオン化エネルギー:電子を取り去るエネルギー
・電子親和力:電子を他の原子から奪い取ろうとするエネルギー
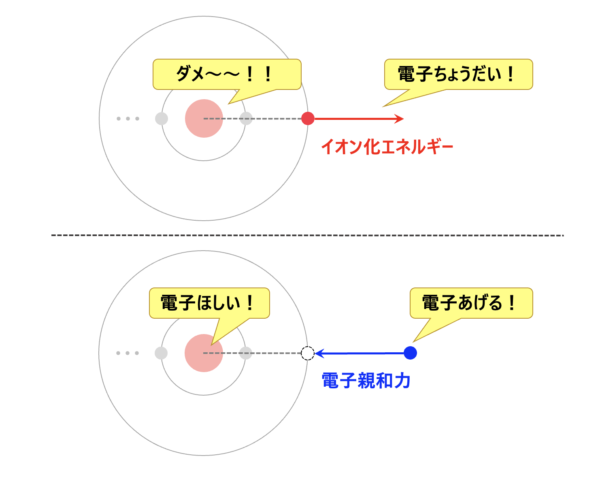
この違いを頭に入れた上で、それぞれ学んでいきましょう。
電子親和力について学びたい方はぜひこちらをご覧ください!

イオン化エネルギーとは?
まずは、イオン化エネルギーの基礎から理解していきましょう。
イオン化エネルギーとは、原子から電子を取り去るのに必要なエネルギーのことをいいます。
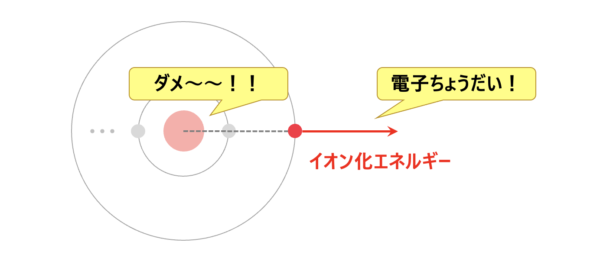
つまり、イオン化エネルギーの大小は、最外殻電子を取り去るのに必要なエネルギーの大小関係と言い換えることができます。
これを頭に入れた上で、周期表をもとにイオン化エネルギーの大小関係を考えてみましょう。
同一族でのイオン化エネルギーの大小関係
それではまず、同一族(周期表の縦)を比較していきましょう。
周期表を縦に見るときのポイントは、
下に\(1\)段いくほど、\(\rm{K}\)殻、\(\rm{L}\)殻、\(\rm{M}\)殻、…というように最外殻が一つずつ大きくなっている
という点です。
つまり、下にいくほど原子半径が大きくなります。
なので、最外殻電子に働く陽子からの引力が小さくなります。
陽子からの引力が小さくなるということは、より簡単に電子をスッと取り去ることができるので、下にいくほどイオン化エネルギーは小さくなります。
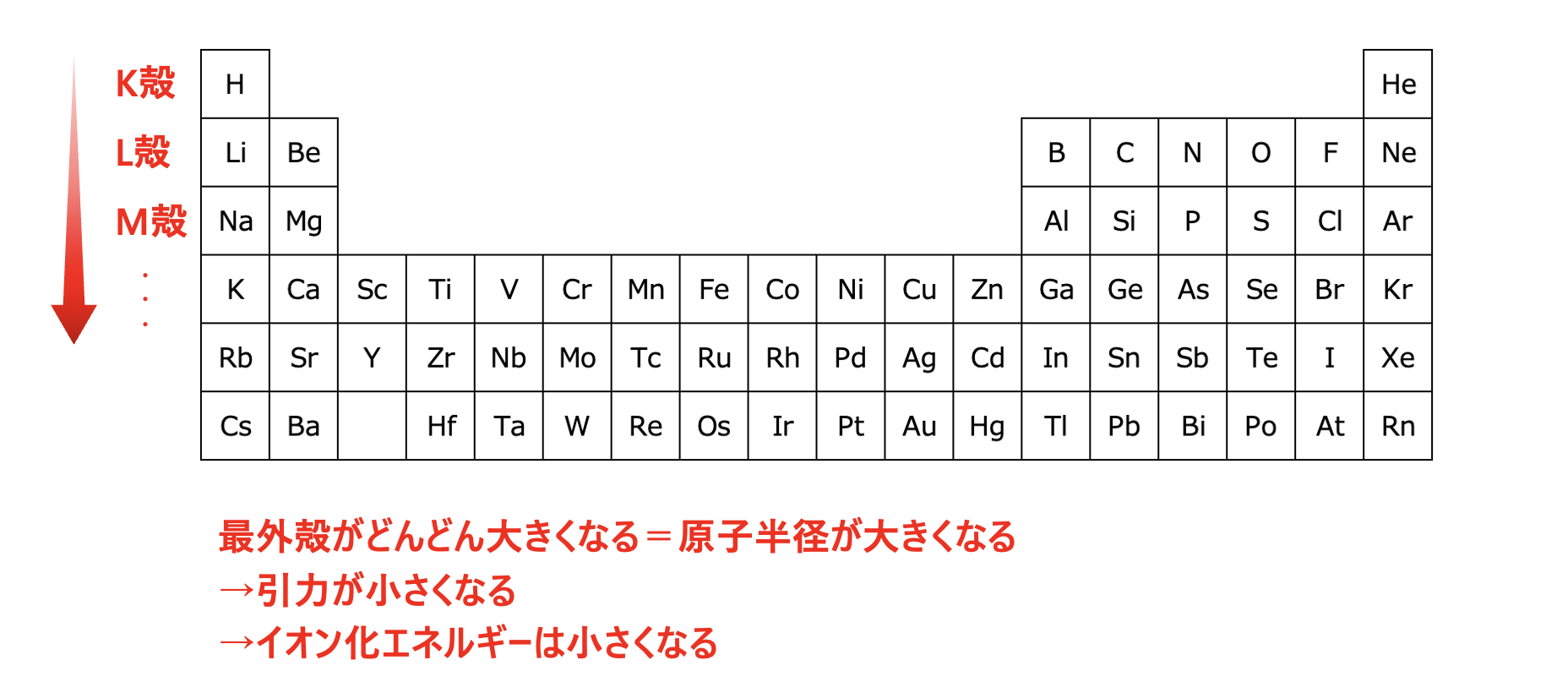
下にいくほど原子半径が大きくなる
→最外殻電子が原子核から遠くなる
→陽子からの引力が小さくなる
→簡単に電子を取り去れる=イオン化エネルギーが小さくなる
同一周期でのイオン化エネルギーの大小関係
次は、同一周期(周期表の横)を比較していきましょう。
同一周期を考えるときのポイントは、
原子半径を考える
ことです。
周期表を横に見たときには、右に行くほど原子半径は小さくなります。
原子半径が小さいということは、最外殻電子に働く引力は強くなるので、電子はより取りにくくなります。
なので、イオン化エネルギーは大きくなります。
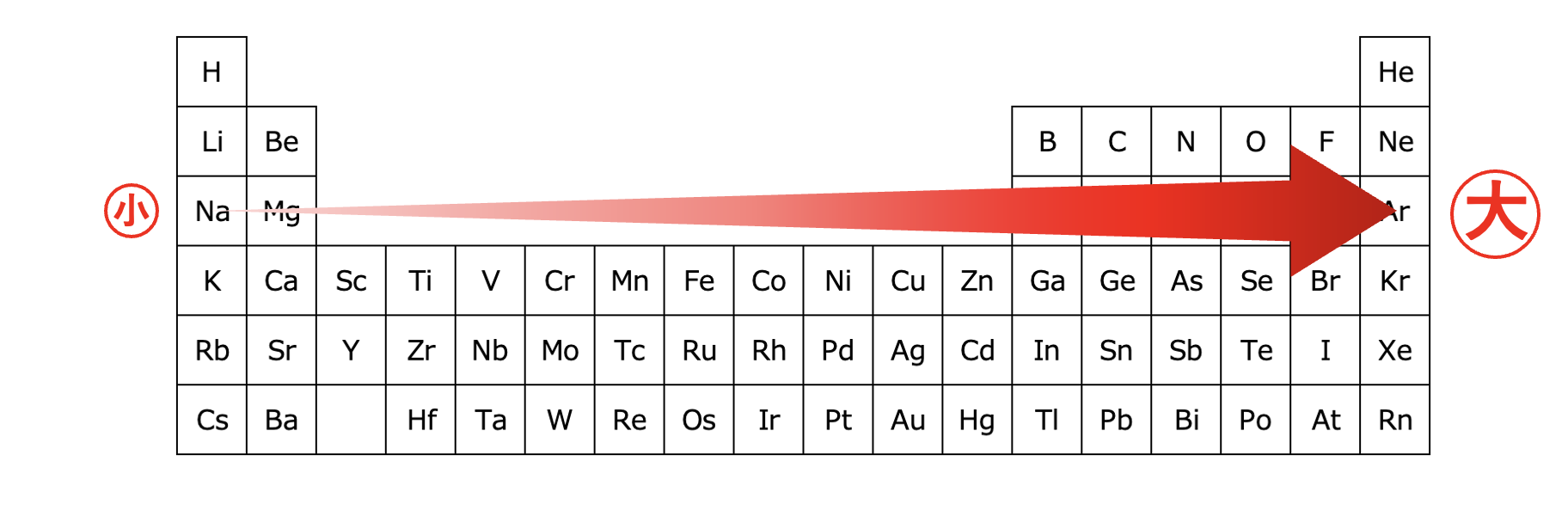
右にいくほど原子半径が小さくなる
→最外殻電子が原子核から近くなる
→陽子からの引力が大きくなる
→電子を取りにくくなる=イオン化エネルギーが大きくなる
原理を理解することで、覚える内容がグンと減るので、しっかりと基礎を理解していきましょう。
イオン化エネルギーの急激な変化
今までの解説で、イオン化エネルギーの大小は理解できたと思います。
では次は、電子を複数取り去ることを考えてみましょう。
ここで、\(\ n\)コ電子を取り去るときのイオン化エネルギーを第\(\ n\)イオン化エネルギーといいます。
つまり、
\(n=\)\(\ 1\)のとき、第\(1\)イオン化エネルギー:電子\(1\)コを取り去るのに必要なエネルギー
\(n=\)\(\ 2\)のとき、第\(2\)イオン化エネルギー:電子\(2\)コを取り去るのに必要なエネルギー
…
というようになります。
そして電子を\(1\)コ取り去ると、原子はマイナス電荷を\(1\)つ失うので、\(1\)価の陽イオンとなります。
そのため、どんどん電子を取り去っていくと、
\(\rm{X→X^+→X^{2+}→…}\)
のように次々とイオン化されていきます。
では、どこまでイオン化されるのでしょうか?
ここで重要なのが、「希ガス配置を見つける!」ということです。
希ガス配置になると非常に安定しているので、そこから電子を取り去るにはとても大きなイオン化エネルギーが必要となります(これは至難の業です…)。
そのため一般的に希ガス配置になるとイオン化は終わってしまいます。
ナトリウム(\(\rm{Na}\))
わかりやすくするために、ナトリウム(\(\rm{Na}\))を考えてみましょう。
\(\rm{Na}\)原子は
\(\rm{K}\)殻:\(2\)個
\(\rm{L}\)殻:\(8\)個
\(\rm{M}\)殻:\(1\)個
の電子配置をしています。
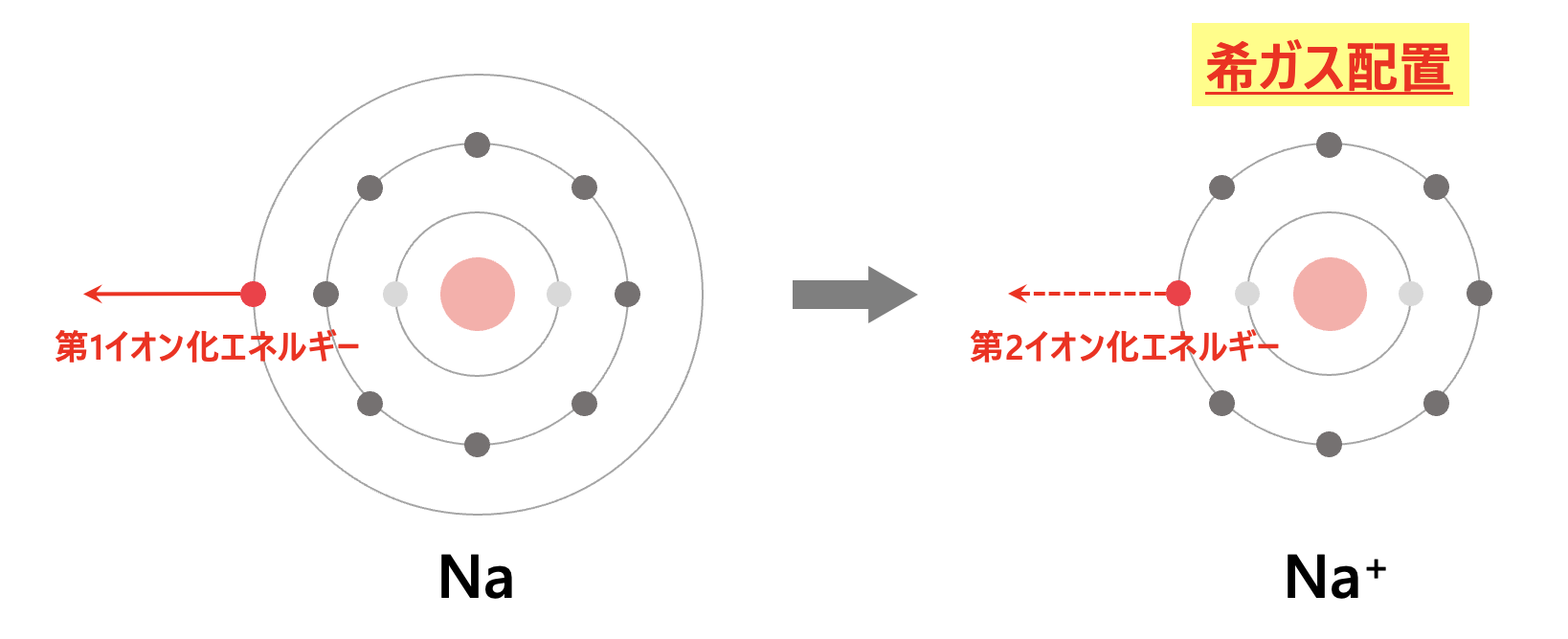
電子を\(1\)個取り去るのはそれほど難しくないので、第\(1\)イオン化エネルギーはそれほど大きな値ではありません。
電子を\(1\)個取ると、\(\rm{Na→Na^+}\)(希ガス配置)になります。
ここから、さらに電子を取り去ることを考えてみましょう。
\(\rm{Na^+}\)は希ガス配置なので、すべての電子の座席が埋まっていて、電子はみんな仲間と共に気持ちのいい状態です。
ここから電子を\(1\)個取り去ろうとすると、みんなが嫌がるので、非常に大きな力が必要になります。
つまり、第\(2\)イオン化エネルギーは非常に大きくなります。
マグネシウム(\(\rm{Mg}\))
もう一つ例として、マグネシウム(\(\rm{Mg}\))を考えてみましょう。
\(\rm{Mg}\)原子は
\(\rm{K}\)殻:\(2\)個
\(\rm{L}\)殻:\(8\)個
\(\rm{M}\)殻:\(2\)個
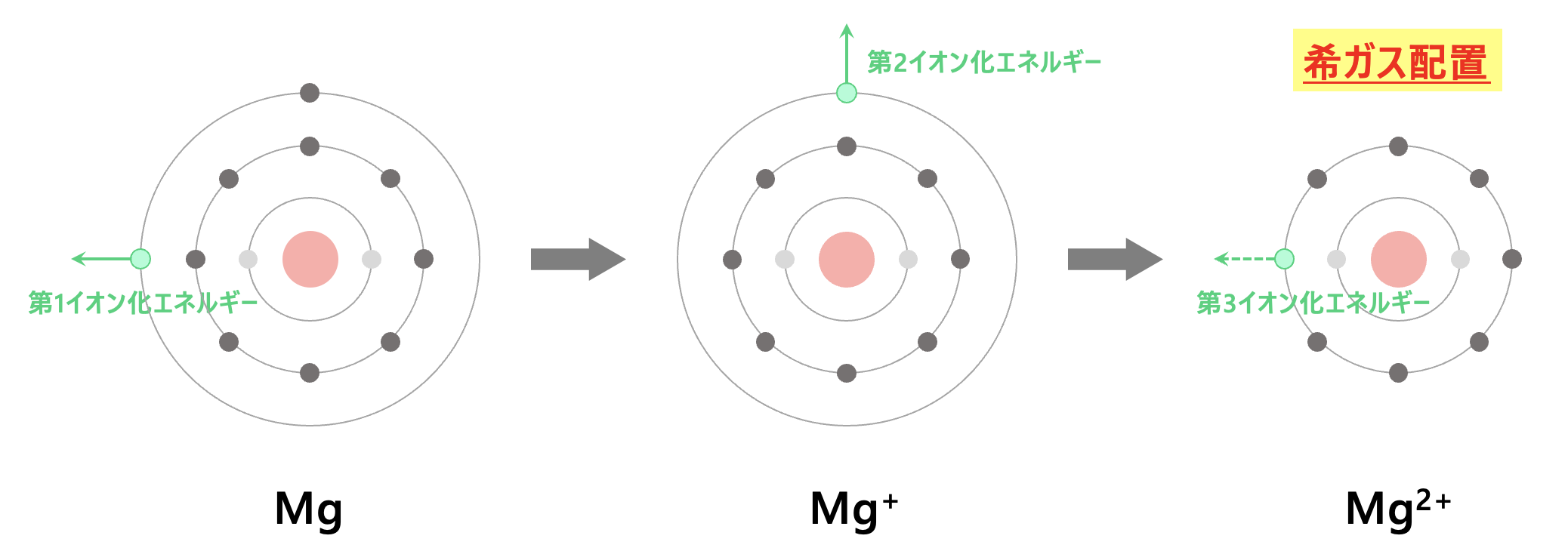
の電子配置をしています。
電子を\(2\)個取り去ると希ガスの電子配置になるので、第\(2\)イオン化エネルギーまでは大きな値ではありません。
そこからさらに電子を取り去ろうとすると、\(\rm{Na}\)原子と同じように非常に大きな力が必要になります。
つまり、第\(3\)イオン化エネルギーは非常に大きくなります。
今までの例を見てきたように、第\(n\)イオン化エネルギーを考えるとき、
族番号の数だけ電子を取り除いたときが希ガス配置
となります。
そしてこの希ガス配置以上に電子を取り去ろうとすると気には大きな力が必要になり、そこでイオン化エネルギーが最大になります。
イオン化エネルギーのまとめ
それではイオン化エネルギーのまとめになります。
周期表を縦と横に分けて考えることで、周期表におけるイオン化エネルギーの特性を理解することができましたね。
イオン化エネルギーを考えるときのポイントは、「原子半径」でした。
これら\(2\)つを組み合わせると、右上にいくほどイオン化エネルギーは大きくなります。
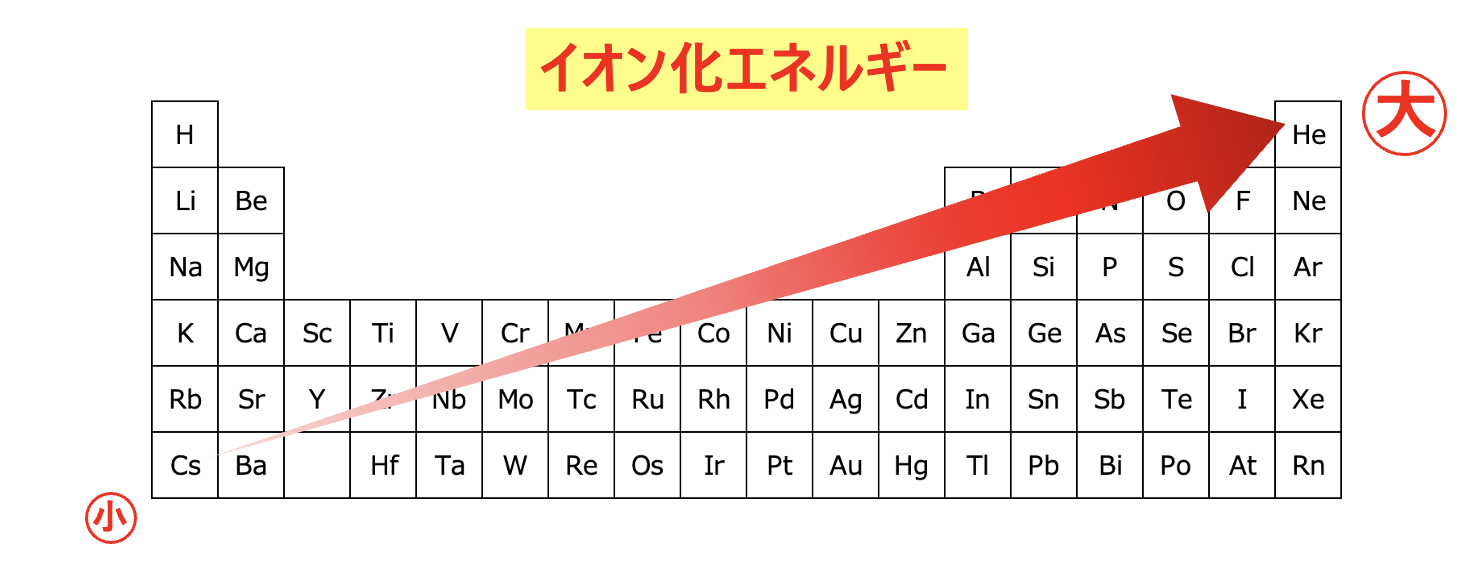
最後に、テストなどによく出てくるイオン化エネルギーのグラフも載せておきますね。
このグラフを見ると、希ガスでイオン化エネルギーが最大になっていることが鮮明にわかると思います。
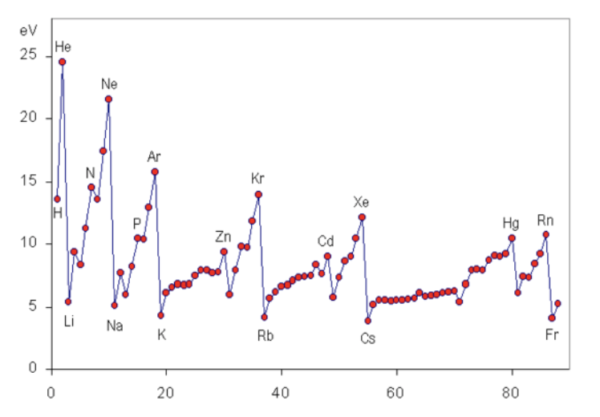
(参考:Wikipedia)



コメント