
- 各\(\rm{pH}\)における等電点の理解
- 実践的な練習問題
を特にポイントとしています.昨日の自分より少しでもレベルアップしていきましょう!
電気泳動
溶液中に電極を入れて電圧をかけることで,電荷を帯びた溶質分子が移動することを電気泳動といいます.この中で,\(\alpha-\)アミノ酸は水溶液の\(\rm{pH}\)によって電荷の帯び方が変わります.そのため\(\alpha-\)アミノ酸の電気泳動は水溶液の\(\rm{pH}\)によって挙動が異なります.
例として中性アミノ酸であるアラニン(\(\rm{Ala}\))を考えてみましょう.
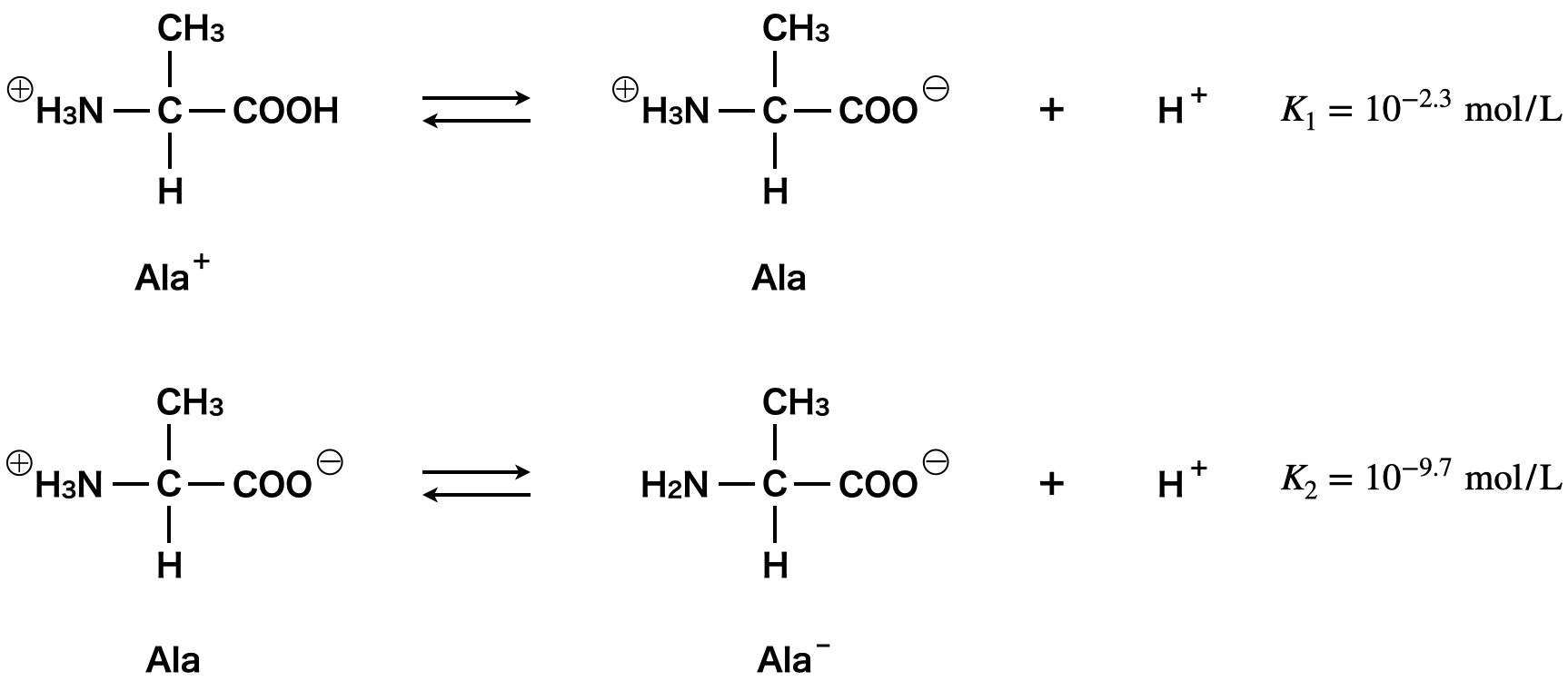
アラニンは溶液の\(\rm{pH}\)変化によって以下のように変化するのでした.
このあたりの内容については前回の記事で詳しく解説しているので,そちらをご覧ください.

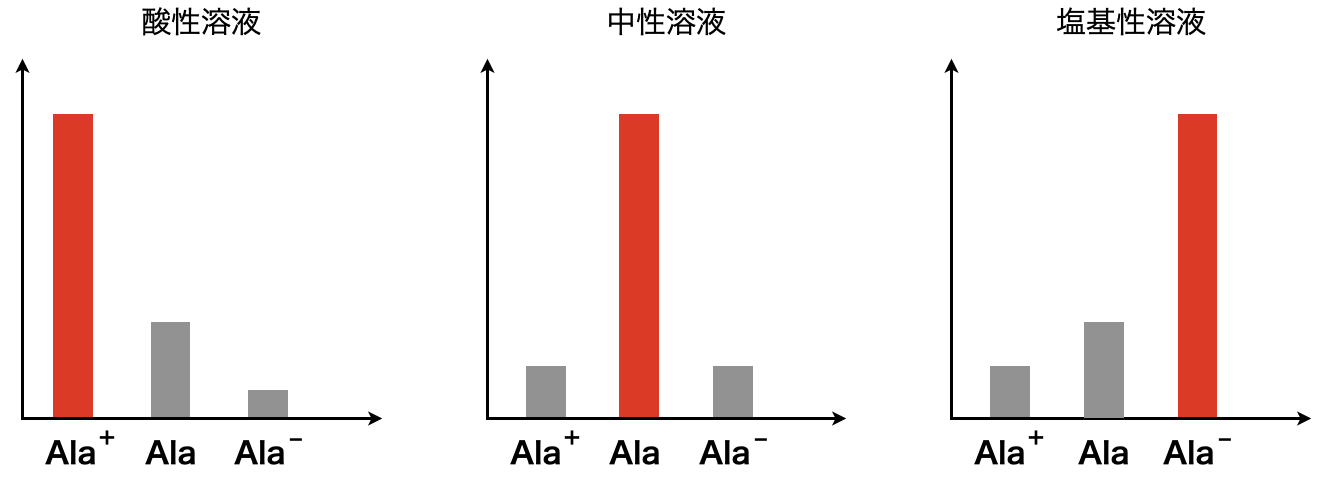
このときの溶液について,\(\rm{Ala^+}\)が大多数である酸性溶液では\(\rm{Ala^+}\)が陰極側へ移動し,塩基性では\(\rm{Ala^-}\)が陽極側へ移動します.また中性では\(\rm{Ala}\)が大多数となるため,電気泳動は起こりにくくなります.図にすると下のようになります!
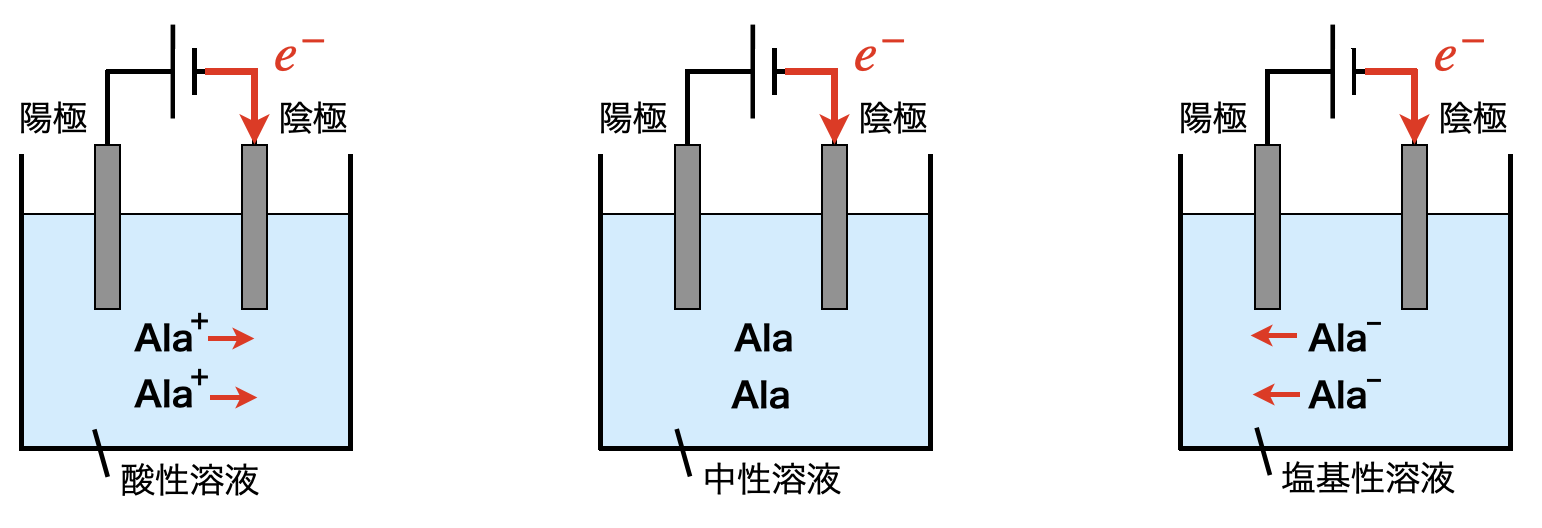
等電点
アニオンになる官能基とカチオンになる官能基の両方をもつ化合物において,化合物全体の電荷の平均が\(0\)となる\(\rm{pH}\)のことを等電点(\(\rm{Isoelectric\ point}\))といいます.このとき電気泳動は起こらないということです.
この考え方としては,「化合物全体の電荷の平均が\(0\)となる」→「アニオン = カチオン」と考えるのがポイントです.そしてこのときの\(\rm{pH}\)を求めるために,今までずっと書いてきたグラフを使って瞬殺していきましょう!
中性アミノ酸の等電点
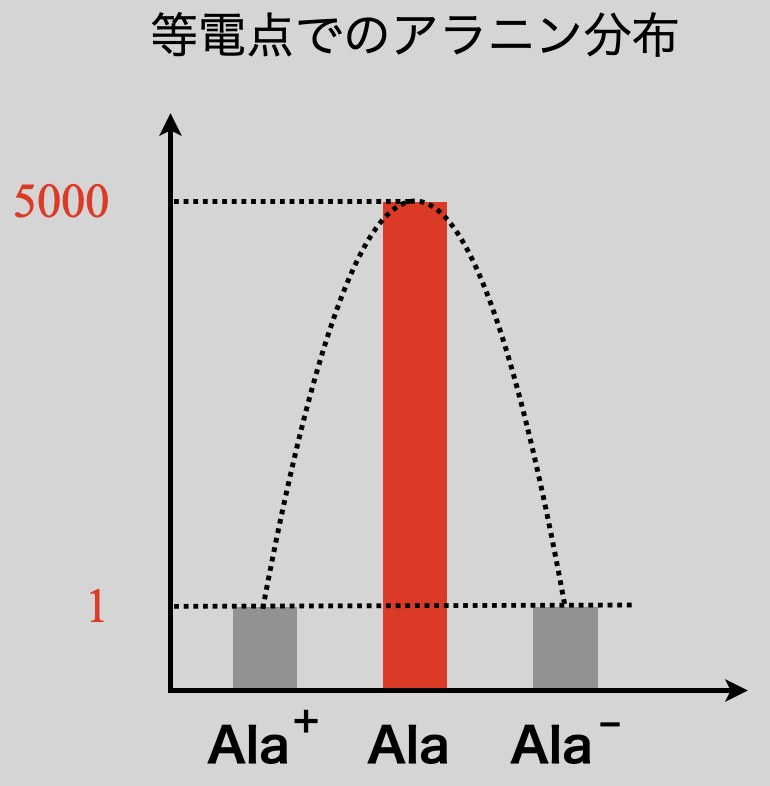
中性アミノ酸であるアラニン(\(\rm{Ala}\))を具体例として考えていきましょう.先ほどの説明からアラニンの等電点とは,\(\rm{[Ala^+] = [Ala^-]}\)となる\(\rm{pH}\)であることがわかります.
図のように\(\rm{[Ala^+] = [Ala^-]}\)のとき,アラニンの分布は左右対称の正規分布になります.このとき\(\rm{[Ala]}\)が最大となります.
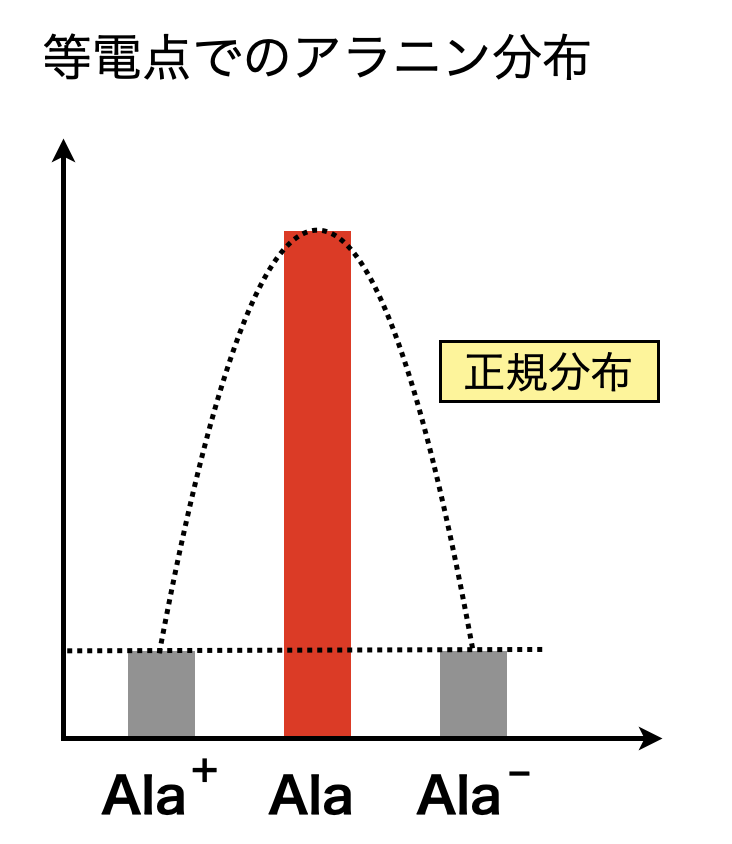
アラニンの電離平衡から平衡定数を考えていきましょう.
\(\rm{Ala^+\ ⇄\ Ala\ +\ H^+}\)
\(\rm{Ala\ ⇄\ Ala^-\ +\ H^+}\)
\(K_1 = \rm{\large \frac{[Ala][H^+]}{[Ala^+]} \small = 10^{-2.3}\ mol/L}\)
\(K_2= \rm{\large \frac{[Ala^-][H^+]}{[Ala]} \small = 10^{-9.7}\ mol/L}\)
ここで,\(\rm{Ala^+}\)と\(\rm{Ala^-}\)の関係性を求めるためには,\(\rm{Ala}\)を消去すれば\(\rm{OK}\)です.ここで覚えておいてほしいのが,中間物質を消去するためには,\(K_1\)と\(K_2\)をかける!ということです.
\(K_1 K_2 = \rm{\large \frac{[Ala^-][H^+]^2}{[Ala^+]} \small = 10^{-12}\ (mol/L)^2}\)
\(\rm{[Ala^+] = [Ala^-]}\)の関係を代入すると,\(\rm{[H^+] = 10^{-6}\ mol/L}\)となり,\(\rm{pH = 6.0}\)であるとわかります.
\(K_1\)を使って,\(\rm{[Ala^+]}\)と\(\rm{[Ala]}\)の比を考えてみましょう.
等電点のとき,\(\rm{[H^+] = 10^{-6}\ mol/L}\)なので,これを\(K_1\)に代入すると,
\(K_1 = \rm{\large \frac{[Ala][H^+]}{[Ala^+]} \small = 10^{-2.3}\ mol/L}\)
\(\rm{\large \frac{[Ala]}{[Ala^+]} \small × 10^{-6} = 10^{-2.3}}\)
\(\rm{\large \frac{[Ala]}{[Ala^+]} \small = 10^{3.7} ≒ 5000 = \large \frac{5000}{1}}\)
つまり,\(\rm{[Ala^+]:[Ala] = 1:5000}\)なので,そのほとんどが\(\rm{Ala}\)になっていることがわかりますね!
酸性アミノ酸の等電点
この勢いのまま酸性アミノ酸も攻略していきましょう.酸性アミノ酸としては,グルタミン酸を考えていきます.
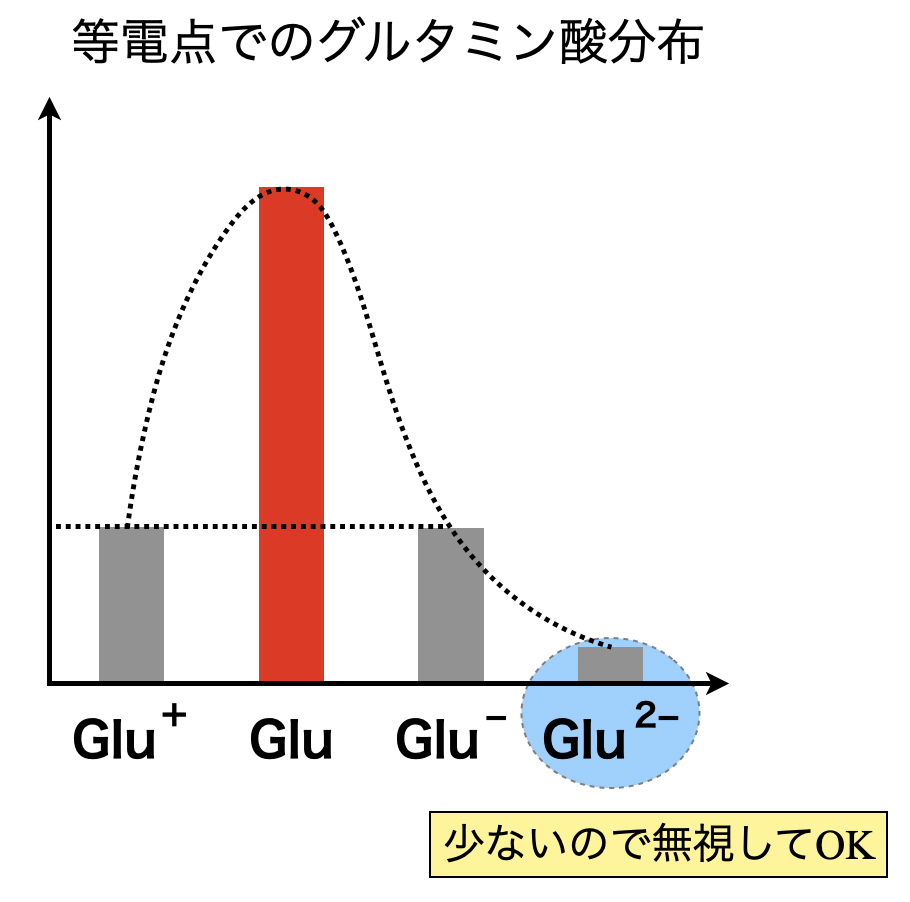
等電点の考え方の復習ですが,アニオン \(=\) カチオンとなる\(\rm{pH}\)を求めていくのでしたね!溶液中のイオンは,\(\rm{[Glu^+]}\),\(\rm{[Glu^-]}\),\(\rm{[Glu^{2-}]}\)であることがわかります.そのため,以下の等式が成り立ちます.
\(\rm{[Glu^+] = [Glu^-] + [Glu^{2-}]}\)
このときグラフを見ると,\(\rm{[Glu^{2-}]}\)は極端に小さいので,無視小であると考えることができます.これを考慮すると,
\(\rm{[Glu^+] = [Glu^-]}\)
という中性アミノ酸とまったく同じ関係式を導くことができましたね!
あとは,\(K_1\)と\(K_2\)から計算していくだけです.
\(\rm{Glu^+\ ⇄\ Glu\ +\ H^+}\)
\(\rm{Glu\ ⇄\ Glu^-\ +\ H^+}\)
\(\rm{Glu^-\ ⇄\ Glu^{2-}\ +\ H^+}\)
\(K_1 = \rm{\large \frac{[Glu][H^+]}{[Glu^+]} \small = 10^{-2.2}\ mol/L}\)
\(K_2 = \rm{\large \frac{[Glu^-][H^+]}{[Glu]} \small = 10^{-4.2}\ mol/L}\)
\(K_3 = \rm{\large \frac{[Glu^{2-}][H^+]}{[Glu^-]} \small = 10^{-9.7}\ mol/L}\)
ここで,\(\rm{[Glu^{2-}]}\)を無視できるということは,第\(3\)電離を無視できるので,\(K_3\)を無視できるということです.
\(K_1 K_2 = \rm{[H^+]^2 = 10^{-2.2} × 10^{-4.2} = 10^{-6.4}\ (mol/L)^2}\)
\(\rm{[H^+] = 1.0 × 10^{-3.2}\ mol/L}\)なので,\(\rm{pH = 3.2}\)となります.
塩基性アミノ酸の等電点
最後にリシンを例として,塩基性アミノ酸の等電点を考えておきましょう.
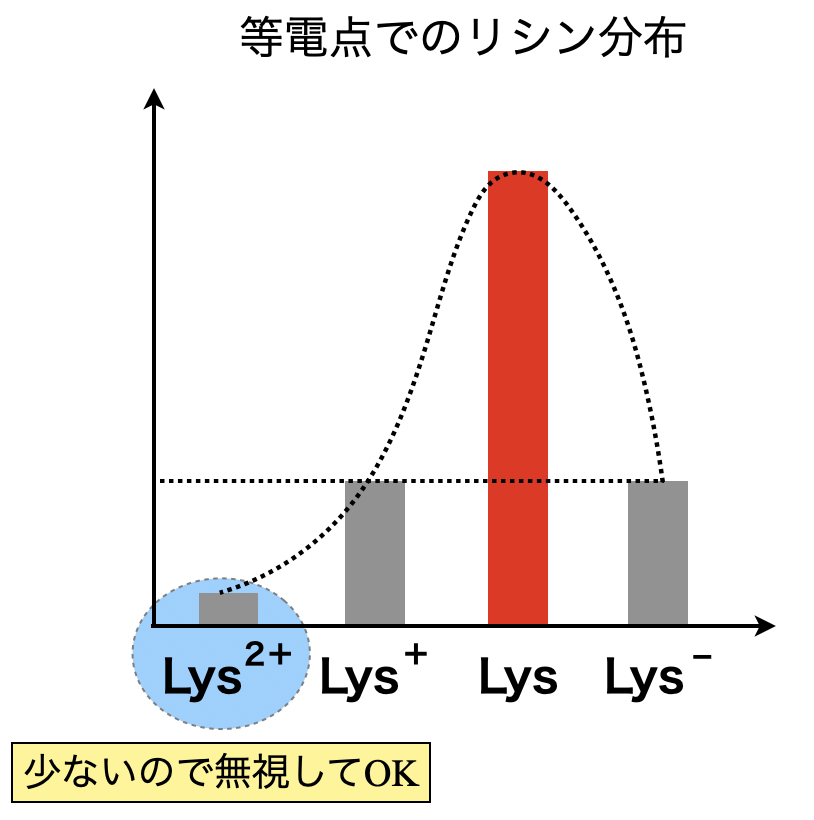
考え方は酸性のときとまったく同じです!リシンの等電点を考えるときは,\(\rm{[Lys]}\)が最大となるときを考えれば\(\rm{OK}\)です.
\(\rm{[Lys^{2+}] + [Lys^+] = [Lys^-]}\)
先ほどと同様に,\(\rm{[Lys^{2+}] ≒ 0}\)と考えることができるので,
\(\rm{[Lys^+] = [Lys^-]}\)
の関係性が成り立ちます.
\(\rm{Lys^{2+}\ ⇄\ Lys^+\ +\ H^+}\)
\(\rm{Lys^+\ ⇄\ Lys\ +\ H^+}\)
\(\rm{Lys\ ⇄\ Lys^-\ +\ H^+}\)
\(K_1 = \rm{\large \frac{[Lys^+][H^+]}{[Lys^{2+}]} \small = 10^{-2.2}\ mol/L}\)
\(K_2 = \rm{\large \frac{[Lys][H^+]}{[Lys^+]} \small = 10^{-8.9}\ mol/L}\)
\(K_3 = \rm{\large \frac{[Lys^-][H^+]}{[Lys]} \small = 10^{-10.3}\ mol/L}\)
ここで,\(\rm{[Lys^{2+}]}\)を無視できるということは,第\(1\)電離を無視できるので,\(K_1\)を無視できるということです.
\(K_2 K_3 = \rm{[H^+]^2 = 10^{-8.9} × 10^{-10.3} = 10^{-19.2}\ (mol/L)^2}\)
\(\rm{[H^+] = 1.0 × 10^{-9.6}\ mol/L}\)なので,\(\rm{pH = 9.6}\)となります.
練習問題
練習問題を解いて,今まで解説してきたことを定着させていきましょう!
グリシンの第\(1\)電離と第\(2\)電離の電離定数は以下の通りである.グリシン(\(\rm{Gly}\))の等電点を求めよ.
\(\rm{Gly^+\ ⇄\ Gly\ +\ H^+}\),\(K_1 = 4.0 × 10^{-3}\ \rm{mol/L}\)
\(\rm{Gly\ ⇄\ Gly^-\ +\ H^+}\),\(K_2 = 2.5 × 10^{-10}\ \rm{mol/L}\)
グリシン(\(\rm{Gly}\))は中性アミノ酸なので,等電点の条件は,\(\rm{[Gly^+] = [Gly^-]}\)ですね.これを求めるためには,不要な\(\rm{Gly}\)を消去していきます.そのためには,\(K_1\)と\(K_2\)をかければ良いのでしたね!
\(K_1 = \rm{\large \frac{[Gly][H^+]}{[Gly^+]} \small = 4.0 × 10^{-3}\ mol/L}\)
\(K_2 = \rm{\large \frac{[Gly^-][H^+]}{[Gly]} \small = 2.5 × 10^{-10}\ mol/L}\)
\(K_1 K_2 = \rm{\large \frac{[Gly^-]}{[Gly^+]} \small [H^+]^2 = 1.0 × 10^{-12}\ (mol/L)^2}\)
ここで,\(\rm{[Gly^+] = [Gly^-]}\)を代入すると,
\(\rm{[H^+] = 1.0 × 10^{-6}\ mol/L}\)なので,\(\rm{pH = 6.0}\)であるとわかります.
この問題は基本的な問題でしたね!次は,より実践的な問題にトライしていきましょう.
グリシンの電離定数は,\(K_1 = 4.0 × 10^{-3}\ \rm{mol/L}\),\(K_2 = 2.5 × 10^{-10}\ \rm{mol/L}\)である.
(\(1\))\(\rm{0.1\ mol/L}\)のグリシン塩酸塩の\(\rm{pH}\)は?
(\(2\))(\(1\))の溶液\(\rm{10\ mL}\)に\(\rm{0.1\ mol/L}\)の\(\rm{NaOH}\)水溶液を\(\rm{5\ mL}\)加えたときの\(\rm{pH}\)は?
(\(3\))(\(1\))の溶液\(\rm{10\ mL}\)に\(\rm{0.1\ mol/L}\)の\(\rm{NaOH}\)水溶液を\(\rm{15\ mL}\)加えたときの\(\rm{pH}\)は?
今回の問題は,酸塩基の問題と似た問題です.同じように瞬殺していきましょう!
このような問題を解く際には,必ずグラフを書いて,自分の立ち位置を確認してから解くようにしてくださいね!今回の滴定曲線を書くと下のようになります.
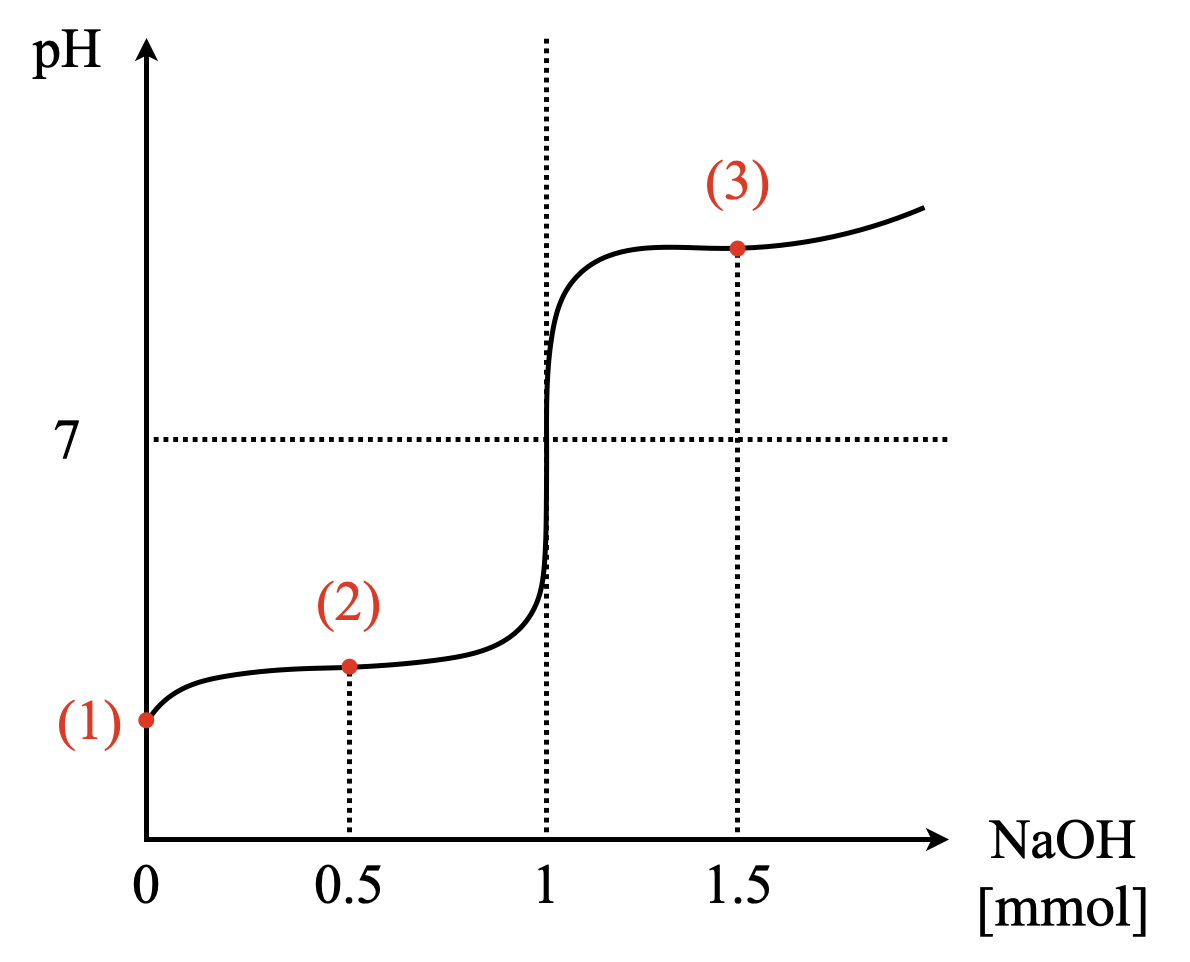
(\(1\))
上の図から,ここは弱酸の\(\rm{[H^+]}\)を求めるときと同じですね!ただし今回は,\(K_1 = 4.0 × 10^{-3}\ \rm{mol/L}\)とかなり大きな値なので,厳密解を用いて解いていきましょう.
グリシンの電離度を\(\alpha\)とすると,下のように整理することができます.
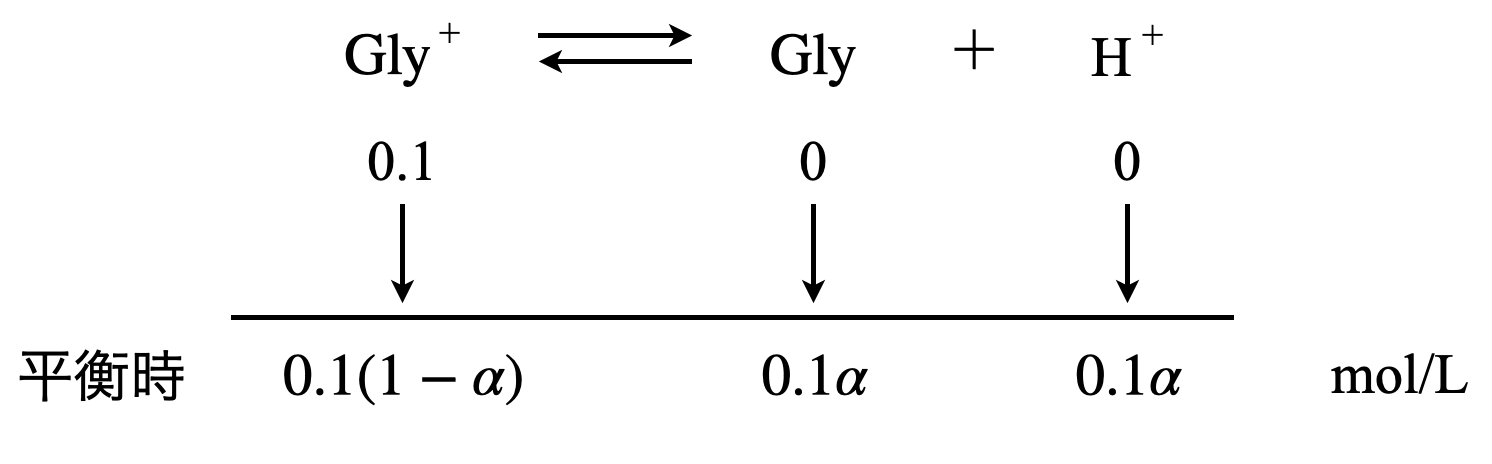
\(K_1 = \large \frac{0.1\alpha\ \cdot\ 0.1\alpha}{0.1(1\ -\ \alpha)} \small = \large \frac{0.1 \alpha^2}{1\ -\ \alpha}\)
\(\alpha^2\ +\ 10K_1 \alpha\ -\ 10K_1 = 0\)
\(\alpha^2\ +\ 4 × 10^{-2}\alpha\ -\ 4 × 10^{-2} = 0\)
これを解くと,\(\alpha = 0.18\)
よって,
\(\rm{[H^+]}\)\( = 0.1 \alpha = 1.8 × 10^{-2}\ \rm{mol/L}\)
したがって,
\({\rm{pH}} =\ – \log_{10}(1.8 × 10^{-2}) = 3\ -\ \log_{10}2 = 1.7\)
(\(2\))
次は,(\(1\))の溶液に\(\rm{NaOH}\)水溶液を\(\rm{5\ mL}\)加えたときを考えていきます.この問題は本当に瞬殺することができます.そのときのポイントは\(2\)点あります.
②物質量(モル)を電離定数に代入する
このたったの\(2\)ステップで完全に攻略することができます.では,実際にやっていきましょう!
現在,\(\rm{Gly}\)が\(\rm{0.1\ mol/L}\)で\(\rm{10\ mL}\)なので,\(\rm{1\ mmol}\)あります.そこへ,\(\rm{NaOH}\)を\(\rm{0.1\ mol/L}\)で\(\rm{5\ mL}\),つまり\(\rm{0.5\ mmol}\)加えたことになります.
次に電離定数について考えていきましょう.
\(K_1 = \rm{\large \frac{[Gly][H^+]}{[Gly^+]}}\)
これを\(\rm{[H^+]}\)について整理すると,
\(\rm{[H^+] = \large \frac{[Gly^+]}{[Gly]} \small }\)\(K_1 = \large \frac{n_{\rm{Gly^+}}}{n_{\rm{Gly}}}\)\( \small K_1\)
上のように,\(n\)(モル)を使って考えることが大切です.これをグラフで整理すると,下のようになります.左側が\(\rm{Gly}\),右側が\(\rm{Gly^+}\)となります.このように視覚的に捉えられるようになることが大切です!
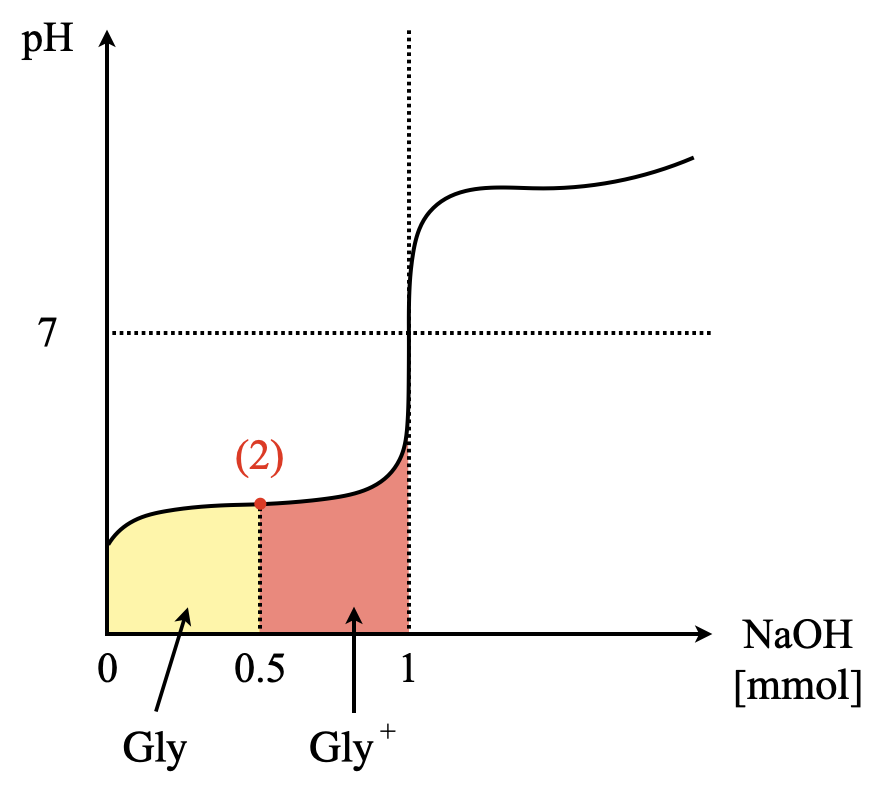
図から,\(\rm{Gly:Gly^+ = 0.5\ mmol:0.5\ mmol = 1:1}\)であることがわかります.これを\(K_1\)に代入すると,
\({\rm{[H^+]}} = \large \frac{1}{1} \small K_1 = 4.0 × 10^{-3}\ \rm{mol/L}\)
よって,
\({\rm{pH}} =\ – \log_{10}(4.0 × 10^{-3}) = 3\ -\ 2\log_{10}2 = 2.4\)
(\(3\))
最後に\(\rm{NaOH}\)水溶液を\(\rm{15\ mL}\)加えたときを考えていきます.このとき,\(\rm{NaOH}\)は\(\rm{1.5\ mmol}\)加えたことになります.
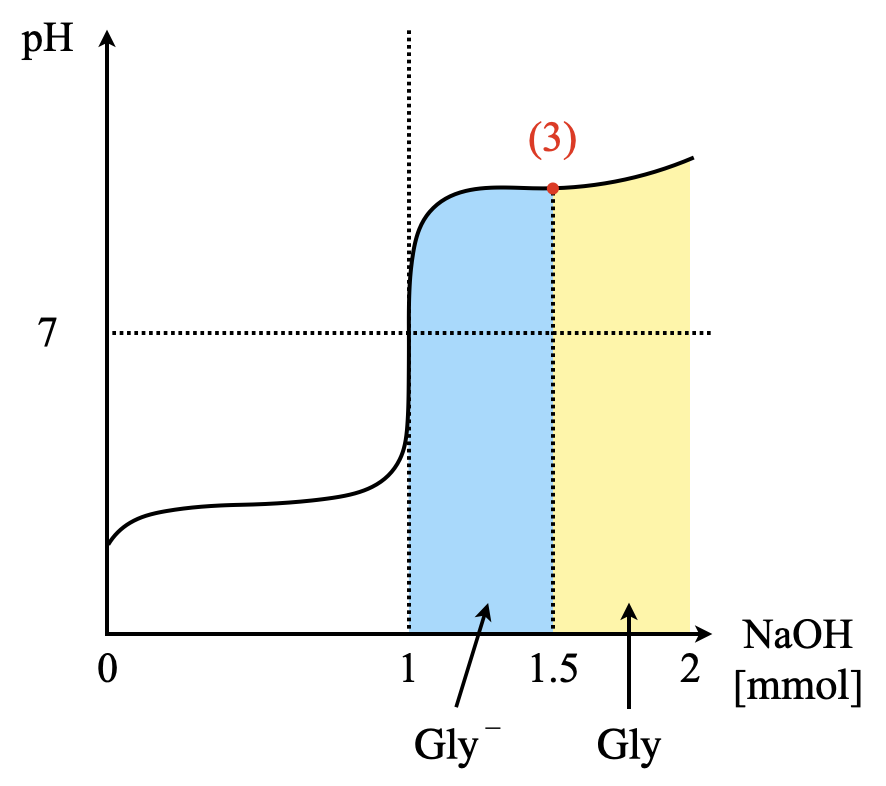
このとき中和点を超えているので,\(K_1\)ではなく\(K_2\)を使う必要があります.ただし,その他の計算方法についてはまったく同じですよ!
\(K_2 = \rm{\large \frac{[Gly^-][H^+]}{[Gly]}}\)
これを\(\rm{[H^+]}\)について整理すると,
\({\rm{[H^+]} = \large \frac{[Gly]}{[Gly^-]}}\)\(\small K_1 = \large \frac{n_{\rm{Gly}}}{n_{\rm{Gly^-}}}\)\(\small K_1\)
図から,\(\rm{Gly^-:Gly = 0.5\ mmol:0.5\ mmol = 1:1}\)であることがわかります.よって,
\(\rm{[H^+] = K_2 = 2.5 × 10^{-10}\ mol/L}\)なので,
\(\rm{pH =\ – \log_{10}(2.5 × 10^{-10}) = 10\ -\ 2\log_{10}2.5 = 9.6}\)となります.
今回はここまでです.
酸塩基の内容がこんなところでも登場するので,しっかりと復習しておいてくださいね!



コメント