
今回は原子半径について解説していきます.
- 同族の原子半径(縦)
- 同一周期の原子半径(横)
に分けて徹底的に解説していきます.昨日の自分より少しでもレベルアップしていきましょう!
原子半径とは
原子半径とは,中心にある原子核から最外殻電子までの距離と考えて大丈夫です!
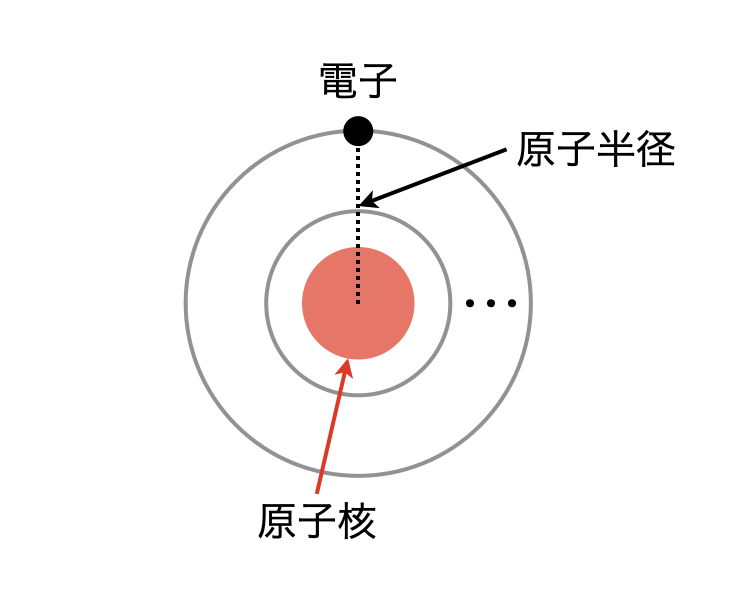
では,その原子半径が周期表でどのような違いがあるのかをわかりやすく解説していきます.周期表で考えていくときには,同一族(縦)と同一周期(横)に分けて考えていくことが大切です.
同一族(縦)における原子半径の大小関係
それではまず周期表を縦方向に見ていきます.
周期表を縦に見るときの最大のポイントは,下に1段いくほどK殻,L殻,M殻,…というように最外殻が大きくなっているという点です.
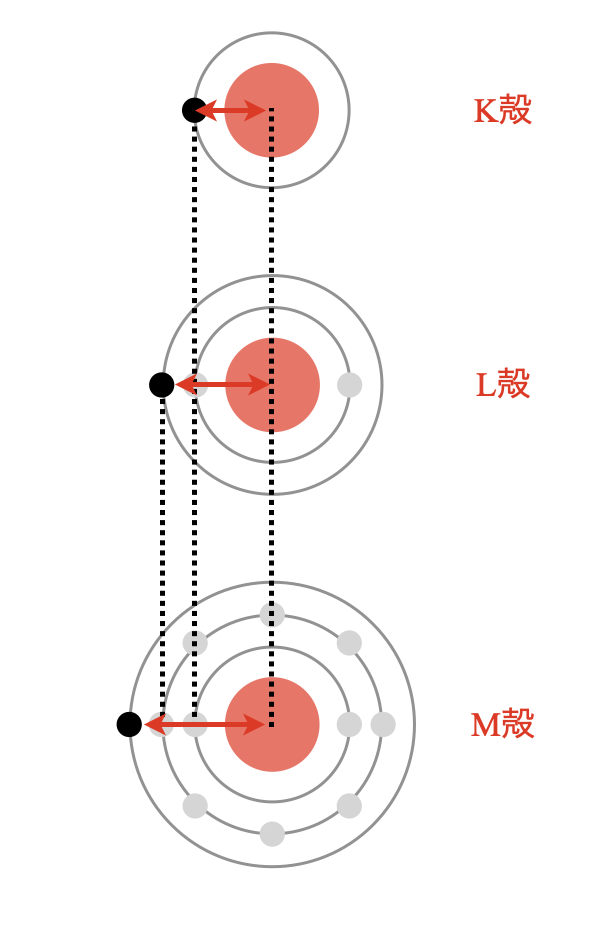
そのため中心から最外殻までの距離が大きくなるので,原子半径も大きくなります.周期表で考えると下のようになります.
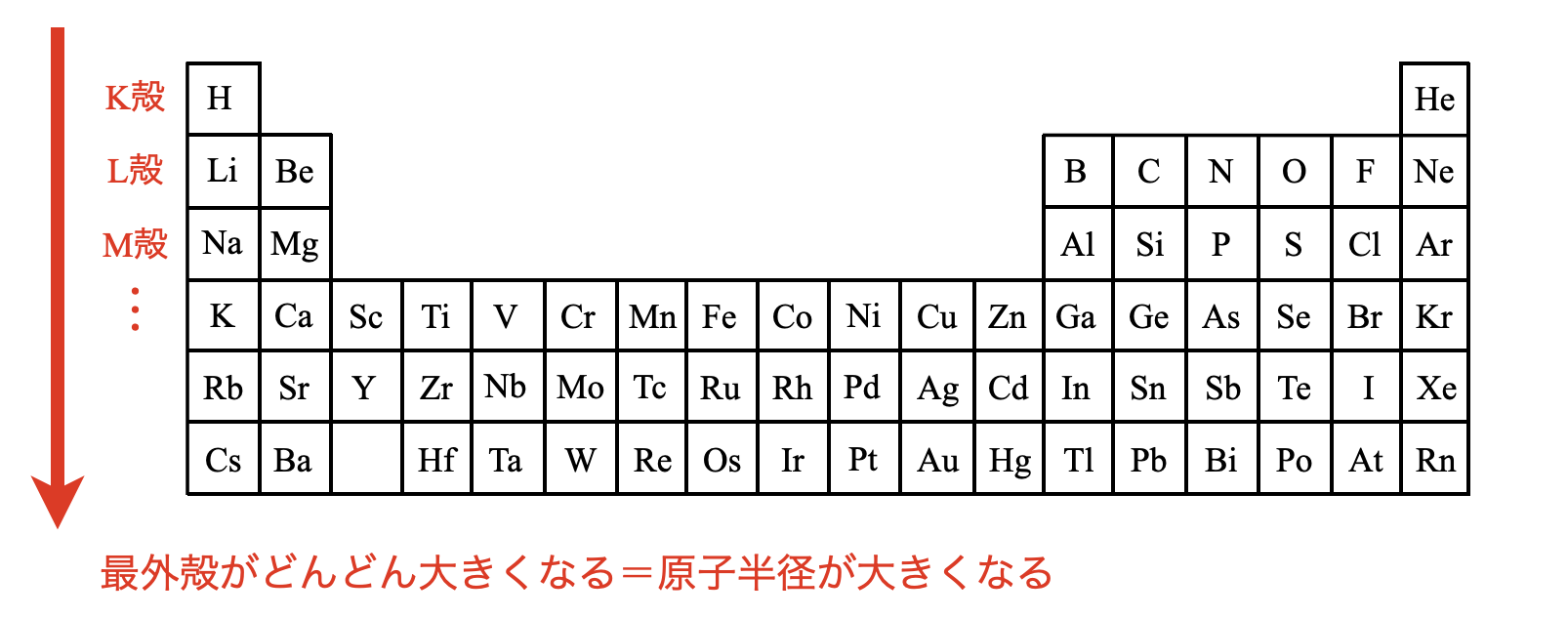
同一周期(横)における原子半径の大小関係
先ほどで同一族に関する原子半径について解説しました.次に,周期表の横方向で原子半径がどのように変化するのかを解説していきます.ここからが本番なので,しっかりとついてきてくださいね!
同一周期では,すべて最外殻は等しくなります.しかしながら異なる点があります.それが原子の中心にある原子核内の陽子の個数です.原子核内の陽子の個数が異なることで,最外殻の電子に働く引力が異なります.
具体例として,\(\rm{Li}\)と\(\rm{Ne}\)を比較してみましょう.
\(\rm{Li}\)は原子番号が\(3\)なので,陽子・電子は\(3\)コあります.この中で最外殻の電子は\(1\)コで,この電子に働く引力を考えます.最外殻に位置する電子は,原子核中の陽子(\(3\)コ)に引き寄せられると同時に,内殻に存在する電子(\(2\)コ)の反発を受けているので,差し引き\(1\)コ(\(= 3\ -\ 2\))の正電荷によって中心に引き寄せられていると考えることができます.
同様にして,\(\rm{Ne}\)も考えていきましょう.\(\rm{Ne}\)は原子番号が\(10\)なので,陽子・電子は\(10\)コあります.この中で最外殻の電子は\(8\)コで,この電子に働く引力を考えます.最外殻に位置する電子は,原子核中の陽子(\(10\)コ)に引き寄せられると同時に,内殻に存在する電子(\(2\)コ)の反発を受けているので,差し引き\(8\)コ(\(= 10\ -\ 2\))の正電荷によって中心に引き寄せられていると考えることができます.
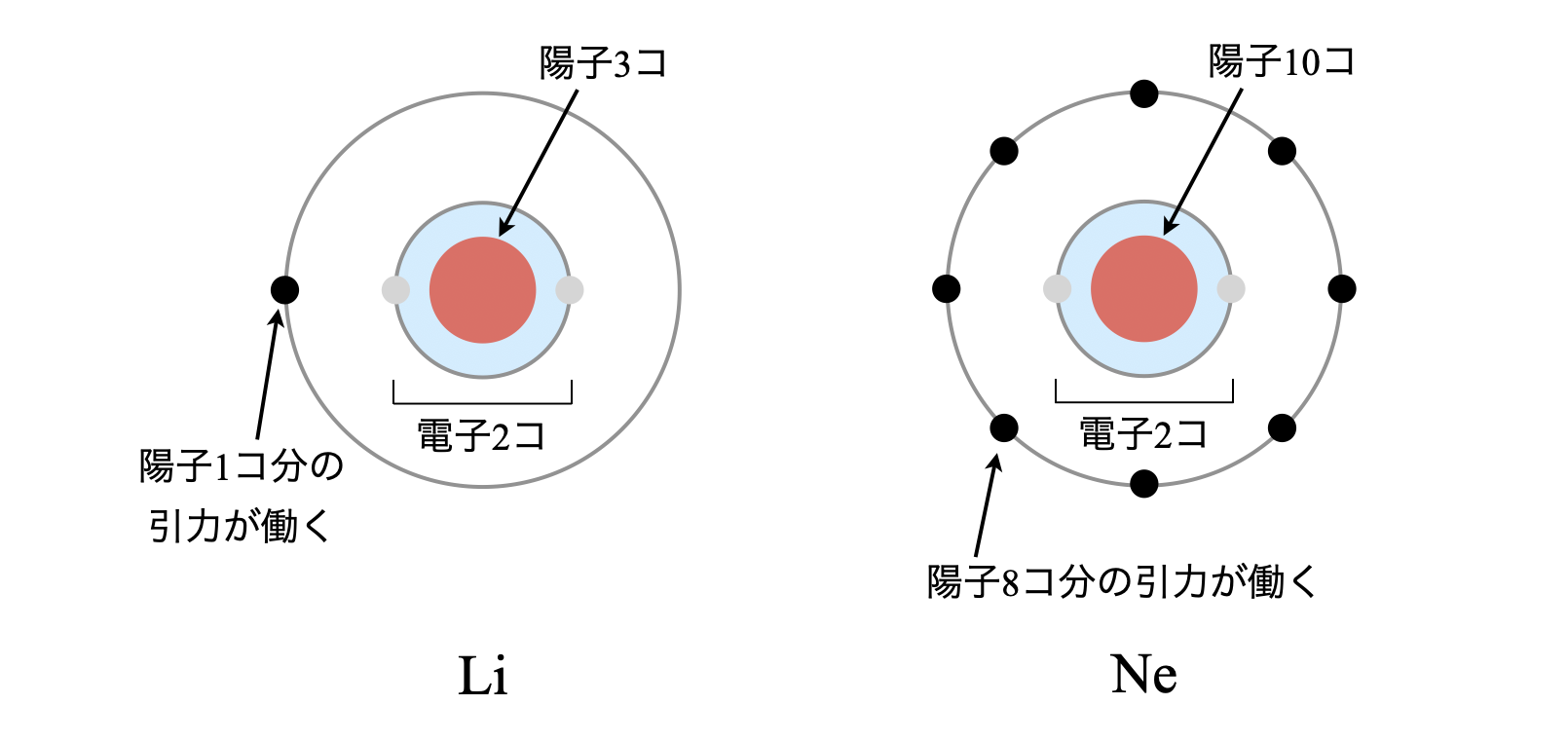
このとき考えた差し引きの正電荷を有効核電荷といいます.つまり,有効核電荷が大きいほど最外殻の電子は内側にギュッと引き付けられやすくなり,結果として原子半径は小さくなります.周期表を横方向で見ていくと,右にいくほどこの有効核電荷が大きくなるので,原子半径は小さくなります.
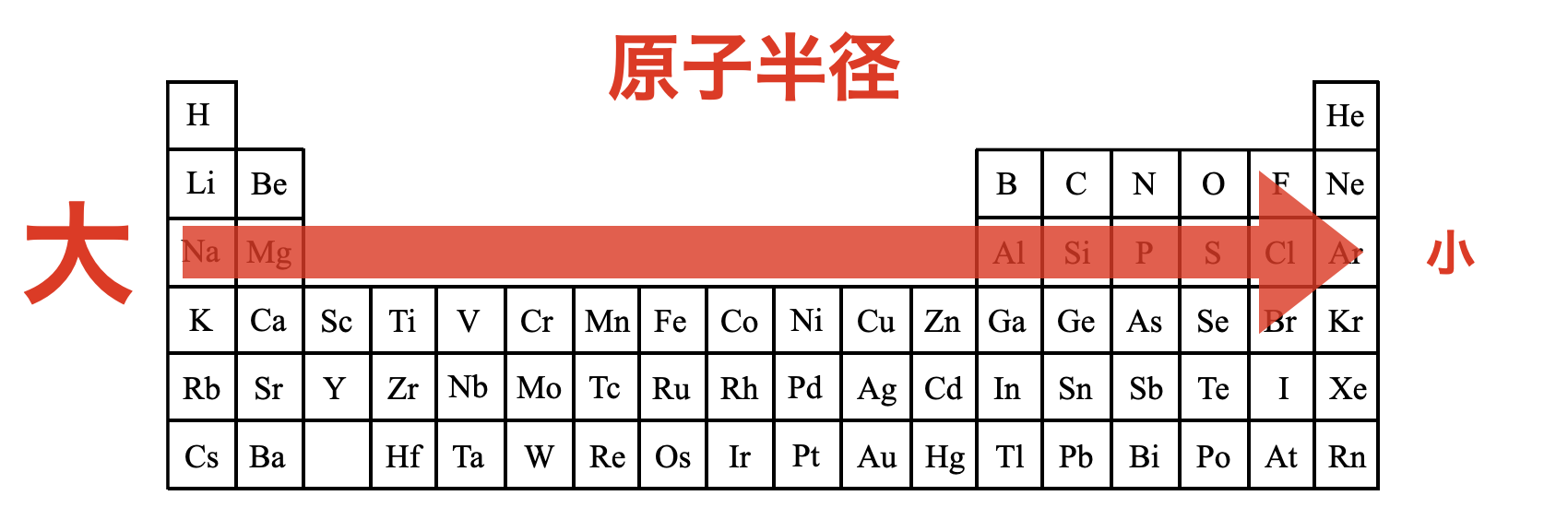
原子半径のまとめ
原子半径を周期表で考えておきましょう!縦方向と横方向を同時に考えると,周期表では原子半径は右上が最小となります.
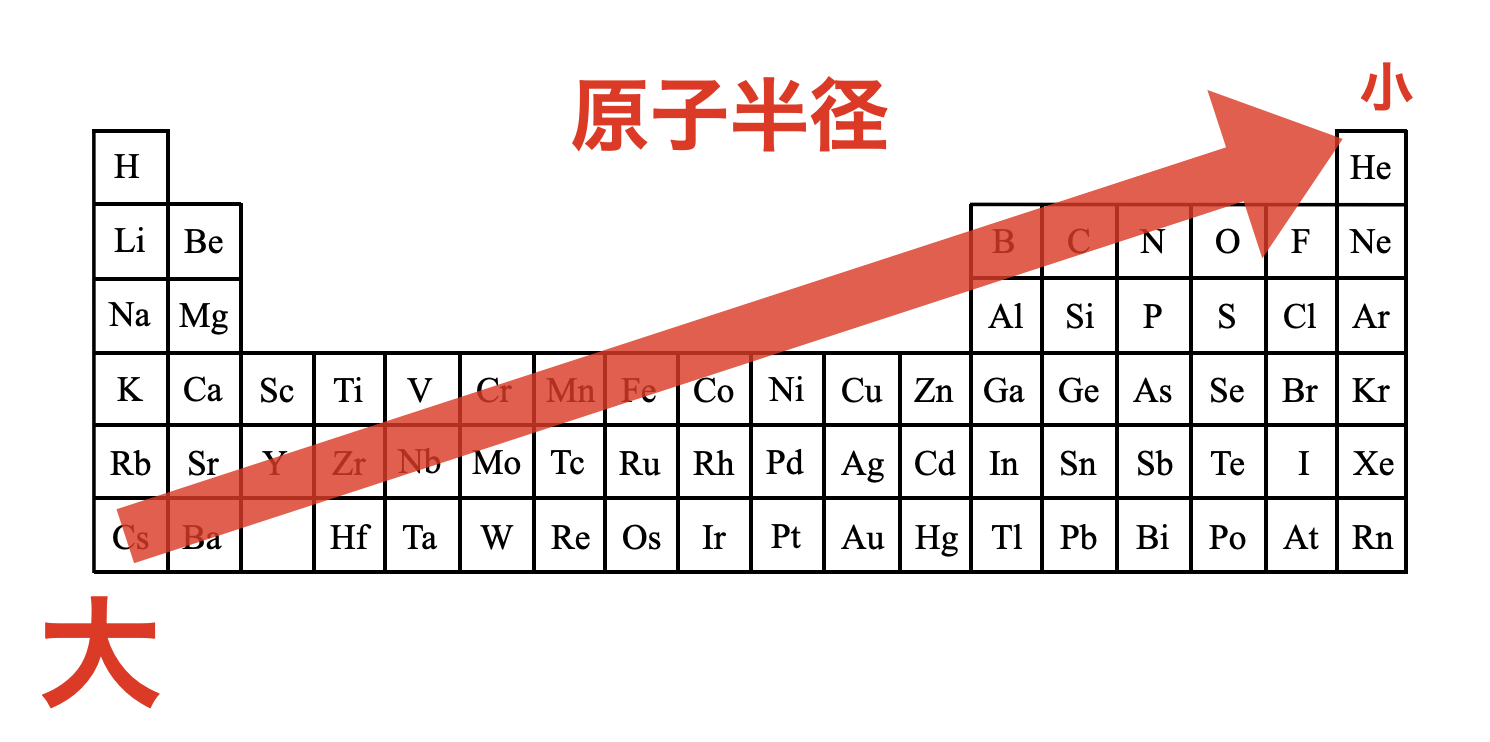
最後にテストでよく出る原子半径のグラフを見ておきましょう!同族元素では,原子番号が大きくなるほど原子半径は大きくなります.そして同一周期では,原子番号が大きくなるほど原子半径は小さくなっています.
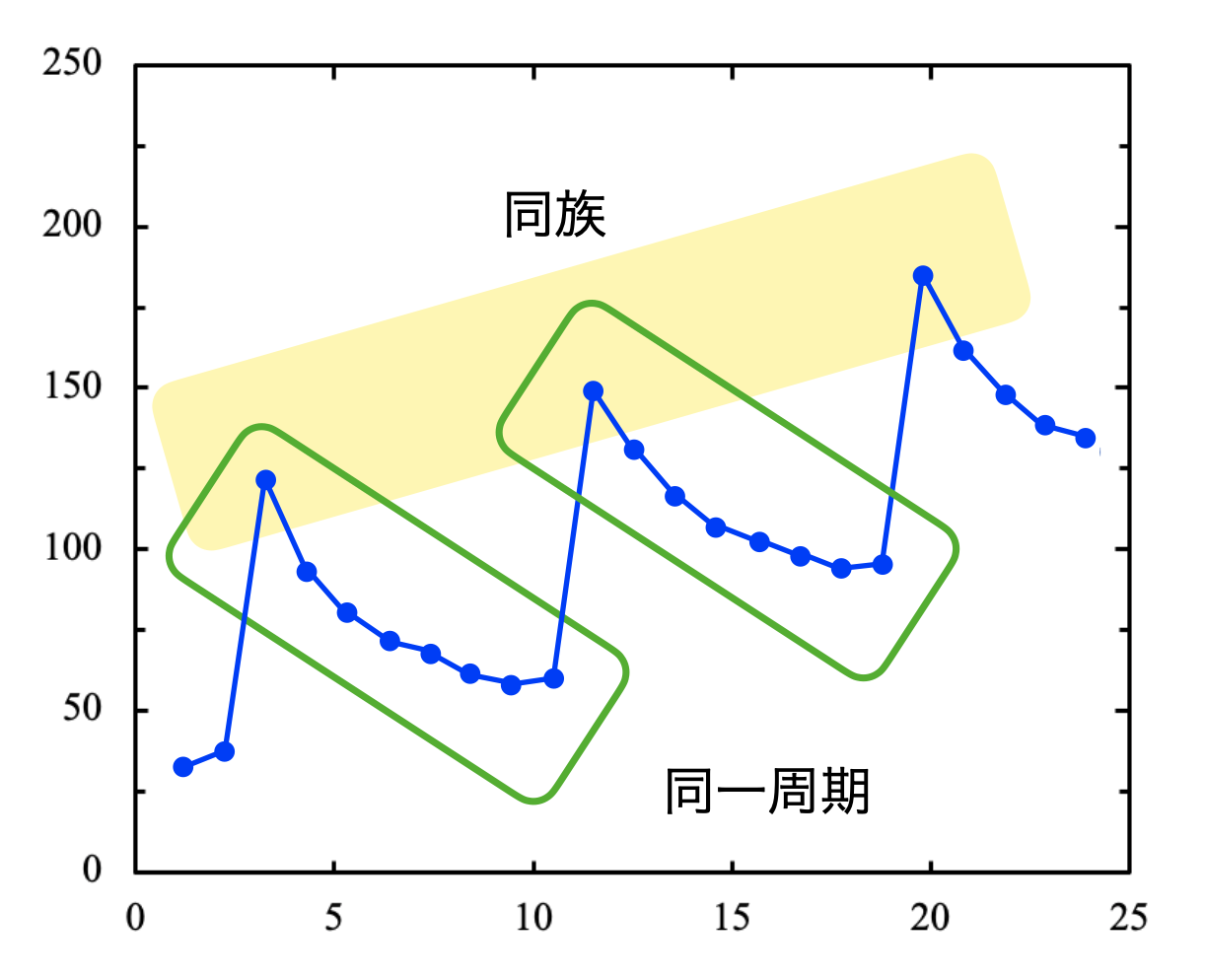
ここで発展的な疑問について紹介します.
「周期表の下にいくほど距離が遠くなるが,その分原子番号が大きくなるので,最外殻の電子が原子の中心に引き付けられる力が強くなるのでは?」という疑問にお答えします.
この問題を理解するポイントは\(2\)点です.
ポイント\(2:\)陽子の電気量と距離の影響力
ポイント1:電子の原子中心に引き付けられる力の求め方
静電気力に関するクーロンの法則をお伝えしましょう.
\(F = k \large \frac{Qq}{r^2}\)
この式の中で,\(Q:\)陽子の電気量,\(q:\)電子の電気量としましょう.ここで今考えているのは,最外殻に位置する電子\(1\)コを取り去るときにどれくらいの力が作用するのかということです.この中で,\(k\)は比例定数,\(q\)は電子\(1\)コの電気量なので,周期表の縦方向で変化することはありません.そのため静電気力\(F\)は原子核の陽子数\(Q\)の\(1\)乗に比例し,距離\(r\)の\(2\)乗に反比例します.
\(F \propto \large \frac{Q}{r^2}\)
ポイント2:陽子の電気量と距離の影響力
先ほど示した比例の式から\(Q\)と\(r^2\)のどちらがより\(F\)に影響を与えるのかを考えましょう.これは当然距離\(r\)が\(2\)乗となっているので,距離の方が影響を与えることがわかります.
これを数式から言葉で説明すると,
周期表を縦に見て下に移動すると,陽子数は増加する(\(Q\)は増加する)
→ただし,距離\(r\)も遠くなる
→距離\(r\)が\(2\)乗なので,より距離の方が影響力が大きくなる
→\(F\)の引力が小さくなる
→原子半径は大きくなる
となります.そのため「同一族(縦)における原子半径の大小関係」で説明したように単純に同一族では下にいくほど原子半径が大きくなるというふうに考えて問題ありませんよ



コメント