【難しいと思いすぎてない？】固体の溶解度|実は1つの解き方ですべて解けます！

KUT

固体の溶解度について解説していきます．

• 溶解度を基本から
• ボックス図を瞬殺で書く

を特にポイントとしています．昨日の自分より少しでもレベルアップしていきましょう！

溶解度の基礎

固体の溶解度について学習を始める前に，どのような種類があるのか？，そしてどのような考え方をすればよいのか？を整理しておきましょう．固体の溶解度の問題は正しく図を書くことができれば確実に得点できるので，しっかりと学んでいきましょう！

 
まず溶解度の考え方についてです．
溶解度とは，一定量の溶媒（\(\rm{100\ g}\)）に溶ける溶質の最大量です．ここで，溶媒・溶質などいろんな言葉が出てきたので復習しておきましょう．

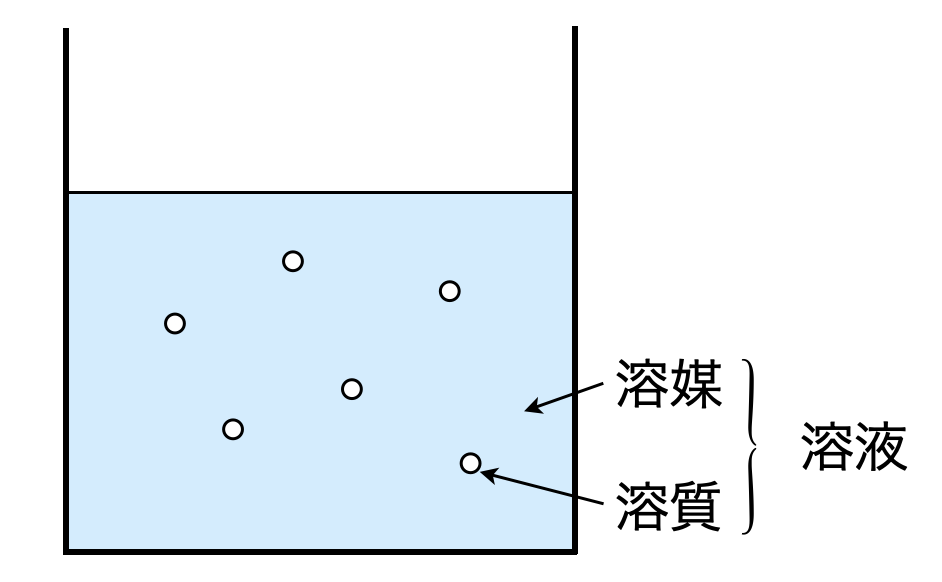
図のように液体中にある物質が混合して均一な液体となる現象を溶解といいます．そして溶液中の各物質には名前があります．
溶けている物質：溶質，溶質を溶かす液体：溶媒，溶質+溶媒：溶液

 
これらの名前は言葉として覚えるのではなく，上図のようなイメージで覚えるようにしましょう！用語を理解すると，溶解度とは一定量の水（\(\rm{100\ g}\)）などにどれだけ溶かすことができるのか？ということになります．

 
溶解度の問題を考えるには，溶かす物質（溶質）の種類によって大きく分けて\(2\)種類あります．

• 単純な物質（水を含まないパターン）
• 水和物（水を含むパターン）

 
水を含むかどうかで，水に溶かしたときに水の量が変化するのでこの\(2\)種類にわけて考える必要があるというわけです．ただ，解き方の本質はどちらも同じなのでまずは単純な物質（水を含まないパターン）から理解していきましょう．

水を含まないパターン

ここでまず溶解度とは，水\(\rm{100\ g}\)に対して溶質（今回は硫酸カリウム）が何\(\rm{g}\)溶けているか？ということです．水\(\rm{100\ g}\)に対しての値という点が重要なのでしっかりとおさえてくださいね！

では，一緒に解いていきましょう！

 
ステップ\(1：\)最初の温度
ステップ\(1\)として，溶液の最初の温度である\(\rm{40^\circ C}\)について考えていきます．
ここで，下のようなボックス図を書いてみましょう．

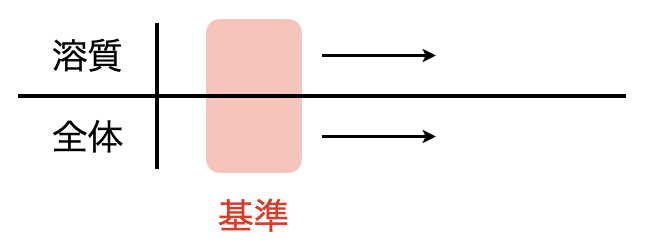
上の段に溶質（今回は硫酸カリウム），下の段に全体と書き，矢印の左側に基準となる値を書いていきます．
基準とは問題で与えられている溶解度のデータのことです．

 
今回の場合は，「\(\rm{40^\circ C}\)で\(60\)」という部分です．\(\rm{40^\circ C}\)で溶質が\(\rm{60\ g}\)溶解するので，溶液全体では\(\rm{160\ g}\)になりますね！

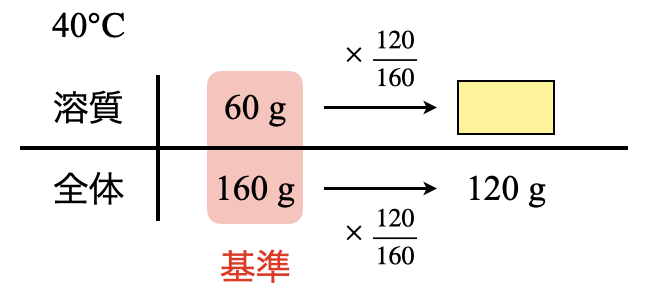
すると，今回の溶液では全体が\(\rm{120\ g}\)なので，このときの溶質の質量を求めることができます．全体を見ると左→右にいくために，\(\large \frac{120}{160}\)かけていることが分かります．そのため，上の段の溶質についても同じように\(\large \frac{120}{160}\)をかけると，溶質の質量を求めることができます．

溶質\(\rm{：60 × \large \frac{120}{160} \small = 45\ g}\)

 
 
ステップ\(2：\)次の温度
次に温度を上げているため，\(\rm{60^\circ C}\)で考えていきます．

\(\rm{60^\circ C}\)についても同じように丁寧に書いていきます．\(\rm{60^\circ C}\)の基準については，「\(\rm{60^\circ C}\)で\(110\)」であることがわかるため，全体は\(\rm{210\ g}\)となります．今回あと溶かすことのできる硫酸カリウムを\(x\ \rm{[g]}\)とします．

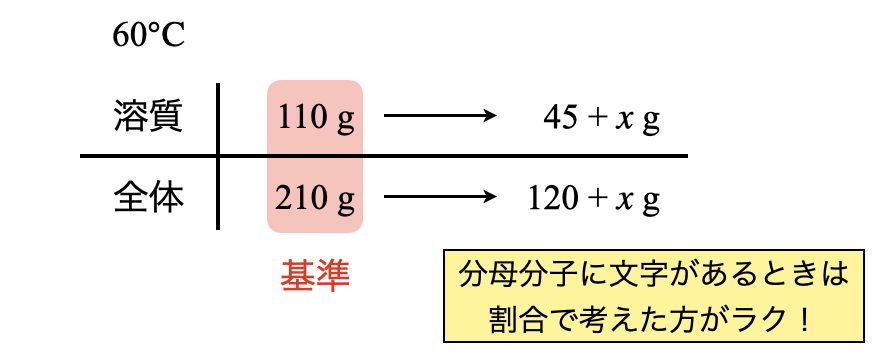
ここで左右の矢印で何倍というふうに考えてもよいのですが，今回は溶質と全体に文字が含まれているので，割合で考えてみましょう．溶質と全体の間に横線があるのですが，これを分母と分子を分ける線というふうに考えます．すると，下のような分数の式を書くことができます．

\(\large \frac{110}{210} \small = \large \frac{45\ +\ x}{120\ +\ x}\)

あとは，この数式を解くと答えを求めることができます．

\(x = 37.5\ \rm{g}\)

水を含むパターン

水を含むパターンは先ほどのパターンよりも若干難しいですが，丁寧に解説していきます！こちらのパターンは色々な角度から問題が出されるため，分けて解説していきます．

溶解度を求める

 
水を含むパターンの中でもパターンに分けて解説していきます．今回はまず溶解度を求める問題です．以下の\(2\)ステップで求めていきます．

 
ステップ\(1：\)溶質・溶媒の質量を求める
溶解させた溶質・溶媒の質量を求めていきます．\(\rm{CuSO_4 \cdot 5H_2O}\)を\(\rm{65\ g}\)溶解させたので，\(\rm{CuSO_4}\)は全体の\(\large \frac{160}{250}\)となります．

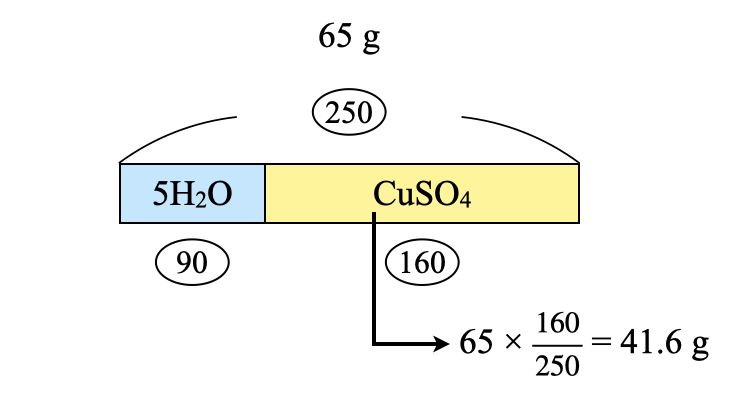
\(\rm{CuSO_4：65 × \large \frac{160}{250} \small = 41.6\ g}\)

\(\rm{H_2O：65\ – 41.6 = 23.4\ g}\)

 
 
ステップ\(2：\)溶解度を求める
溶解度を求めるために，先ほどと同じようにボックス図を書いていきます．

ただし，ここで例外があります．溶解度を求めるときは，下の段を水にしてください！これは，溶解度の基準が溶液全体ではなく，水であるためです．

 
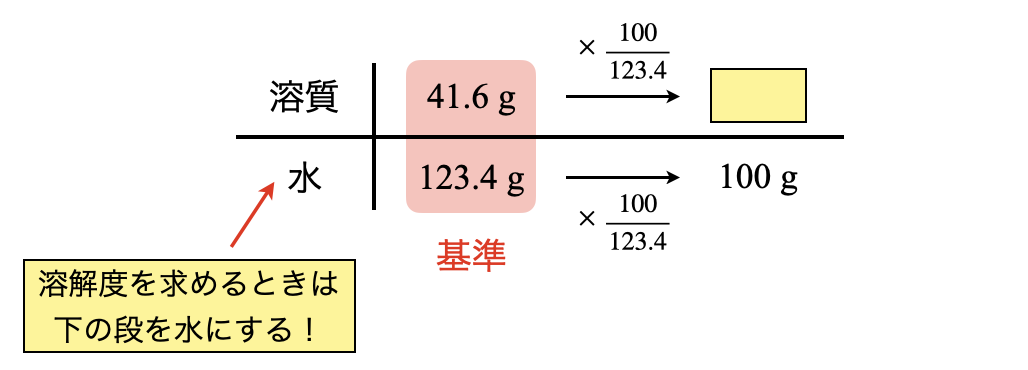
全体を見ると左→右にいくために，\(\large \frac{100}{123.4}\)かけていることが分かります．そのため，上の段の溶質についても同じように\(\large \frac{100}{123.4}\)をかけると，溶質の質量を求めることができます．

溶質\(\rm{：41.6 × \large \frac{100}{123.4} \small = 33.7\ g}\)

水\(\rm{100\ g}\)に対して溶質が\(\rm{33.7\ g}\)溶解するため，この\(33.7\)がそのまま溶解度ということになります．溶解度を求めるときには，「下の段を水にする！」という点にだけ注意してくださいね！

溶質を何\(\rm{g}\)入れる？

次は，必要な\(\rm{CuSO_4 \cdot 5H_2O}\)の質量を求める問題です．

 
ステップ\(1：\)飽和溶液\(\rm{100\ g}\)中に含まれる\(\rm{CuSO_4}\)を求める
まず，飽和溶液\(\rm{100\ g}\)中に含まれる\(\rm{CuSO_4}\)を求めます．ここでのボックス図は今までと同じように，下の段は「全体」で考えます！

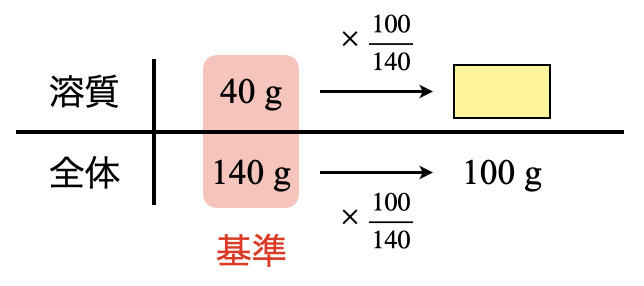
これからいつもの要領で溶質（\(\rm{CuSO_4}\)）を求めましょう！

溶質\(\rm{：40 × \large \frac{100}{140} \small = 28.6\ g}\)

 
 
ステップ\(\rm{2：CuSO_4→CuSO_4 \cdot 5H_2O}\)に変換！
先ほど求めた\(\rm{CuSO_4}\)の質量を\(\rm{CuSO_4 \cdot 5H_2O}\)に変換しましょう！

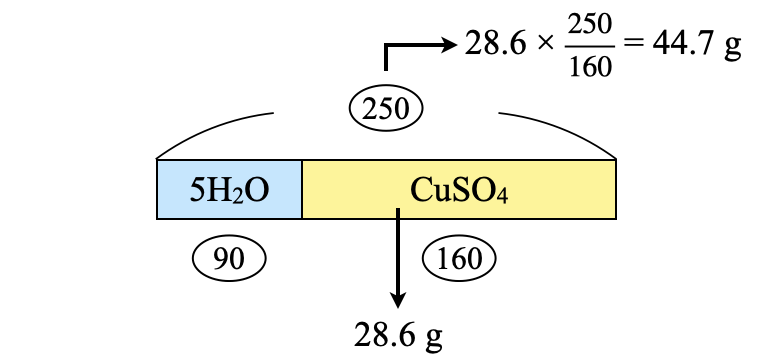
\(\rm{CuSO_4 \cdot 5H_2O：28.6 × \large \frac{250}{160} \small = 44.7\ g}\)

今回の問題は先ほどの練習問題\(2-1\)と逆のステップになっていますね！

水和物の析出

 
冷却によって水和物を析出する場合，残った水はその水和水の質量分だけ減少します．先ほどの飽和水溶液を冷却することで，\(\rm{CuSO_4 \cdot 5H_2O}\)の析出する質量を求めます．

 
析出する\(\rm{CuSO_4 \cdot 5H_2O}\)の質量を\(y\ \rm{[g]}\)とします．このとき析出する\(\rm{CuSO_4}\)（溶質）は，\(\large \frac{160}{250} \small y\ \rm{[g]}\)となります．これをふまえた上でボックス図を書いていきます．

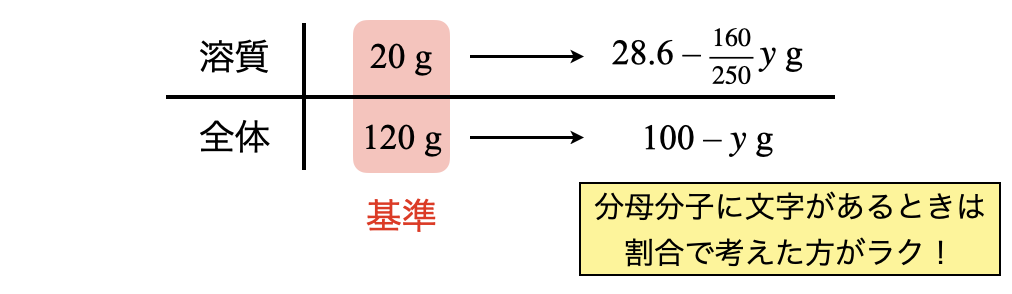
今回も分母分子に文字が含まれているので，割合で考えます！

\(\large \frac{20}{120} \small = \large \frac{28.6\ -\ \frac{160}{250}y}{100\ -\ y}\)

これを解くことで，\(y\)を求めます．

\(100\ – y = 6 (28.6\ – \large \frac{16}{25} \small y)\)

\(2500\ – 25y = 150(28.6\ – 16y)\)

\(y = 25.2\ \rm{g}\)

 
 
 
今回はここまでとなります．
固体の溶解度の問題は水を含む・含まないの\(2\)パターンありますが，どちらもボックス図で攻略することができます．何度も練習して確実に溶けるようにしておきましょう！