緩衝溶液（実践編）

理論化学

2021.09.17 2020.12.02

この記事は約7分で読めます。

今回は，緩衝溶液の実践編になります．
実際の計算問題について習得していきましょう！

緩衝溶液の解説編についてはこちらにあります．
緩衝溶液の基礎をまだ理解できていない方は，是非こちらからご覧ください．
緩衝溶液（解説編）

それでは今日も頑張っていきましょう！

緩衝溶液（パターン1）
緩衝溶液（パターン2）
緩衝溶液（パターン3）

緩衝溶液（パターン1）

今回は以下の問題について考えていきましょう．

\(0.1\ \rm{mol/L}\)の\(\rm{CH_3COOH}\ 10\ \rm{mL}\)と\(0.1\ \rm{mol/L}\)の\(\rm{CH_3COONa}\ 20\ \rm{mL}\)の溶液の\([\rm{H}]^+\)は？
\(\rm{CH_3COOH}\)の\(K_{\rm{a}} = 2.0 × 10^{-5}\ \rm{mol/L}\)

こちらの溶液は\(\rm{CH_3COOH}\)と\(\rm{CH_3COONa}\)の混合であるため，緩衝溶液です．
緩衝溶液の平衡定数は，以下のようになります．

\(K_{\rm{a}} = \large \frac{n_{\rm{CH_3COO}^-}}{n_{\rm{CH_3COOH}}} \small [\rm{H}^+] \)

\(\rm{CH_3COOH}\)のモル \(= 0.1 × 10 = 1.0\ \rm{mmol}\)
\(\rm{CH_3COO}^-\)のモル \(= 0.1 × 20 = 2.0\ \rm{mmol}\)

ここで，「mmol」という単位を使うことがポイントです！！

【mmolについて】
「mmol」という単位が出てきましたが，タイプミスではありませんよ！
「mm」や「mg」などはみなさん使ったことありますよね！？
この「m」は10^-3倍という意味です．
なので，答案で書かなければ，自分で考える上ではこちらの方が計算しやすくベターです！

これから\([\rm{H}^+]\)を求めることができます．

\(K_{\rm{a}} = \large \frac{2.0}{1.0} \small [\rm{H}^+] = 2.0 × 10^{-5}\)
\([\rm{H}^+] = 1.0 × 10^{-5}\ \rm{mol/L}\)

このように解くと，非常に簡単に解けますね！！

先程の溶液に\(0.1\ \rm{mol/L}\)の\(\rm{HCl}\ 1\ \rm{mL}\)加えたときの\([\rm{H}^+]\)は？

今回の溶液に加えた\(\rm{HCl}\)の物質量をまず初めに計算しておきましょう！
\(\rm{HCl}\)のモル\( = 0.1 × 1 = 0.1\ \rm{mmol}\)

\(\rm{CH_3COOH}\ +\ \rm{CH_3COONa}\)の溶液に\(\rm{HCl}\)を加えると，以下の反応が進行します．

CH₃COONa　+　HCl　→　CH₃COOH　+　NaCl

この反応での物質量変化を考えてみましょう！

【反応が\(0.1\ \rm{mmol}\)進行する理由】

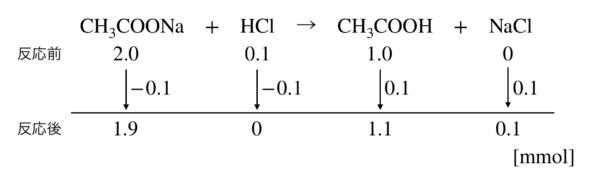
上の反応式では，\(\rm{NaCl}\)の反応前が\(0\)となっているため，反応が進行します．
\(\rm{CH_3COONa}\)と\(\rm{HCl}\)で先に「\(0\)」となったところで反応は終了します．
そのため上の反応式では，反応が\(0.1\ \rm{mmol}\)だけ進行しています．

これから
\(K_{\rm{a}} = \large \frac{1.9}{1.1} \small [\rm{H}^+] = 2.0 × 10^{-5}\)
\([\rm{H}^+] = 1.06 × 10^{-5}\ \rm{mol/L}\)
と求まります．

ここで，\([\rm{H}^+]\)を比較してみましょう．
ほとんど\([\rm{H}^+]\)が変化していないことが分かりますね！
\(\rm{pH}\)に直すと，\(0.03\)しか変化していないことになります．
これが緩衝溶液の効果となります．

緩衝溶液（パターン2）

では，次のパターンの問題を解いていきましょう．
先程とは少し違いますが，解き方は同じですよ！

\(0.1\ \rm{mol/L}\)の\(\rm{CH_3COOH}\ 10\ \rm{mL}\)と\(0.1\ \rm{mol/L}\)の\(\rm{NaOH}\ 4\ \rm{mL}\)の溶液の\([\rm{H}^+]\)は？
\(\rm{CH_3COOH}\)の\(K_{\rm{a}} = 2.0 × 10^{-5}\ \rm{mol/L}\)

今回の問題は一見するとどのように解けばよいかわからないかもしれません，
しかし，一緒に考えていきましょう！

\(\rm{CH_3COOH}\)の一部が\(\rm{NaOH}\)と中和反応し，\(\rm{CH_3COONa}\)が生成されます．
ということは，溶液中には\(\rm{CH_3COOH}\)と\(\rm{CH_3COONa}\)が存在するため，緩衝溶液ですね！

CH₃COOH　+ NaOH → CH₃COONa + H₂O

こちらの反応式の物質量変化を見てみましょう．

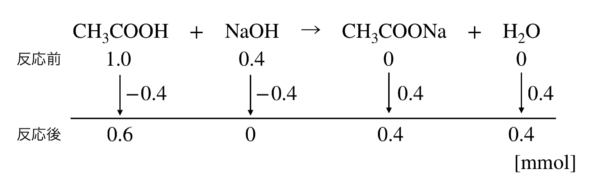
これより，
\(\rm{CH_3COOH}\)のモル \(= 0.6\ \rm{mmol}\)
\(\rm{CH_3COONa}\)のモル \(= 0.4\ \rm{mmol}\)
となりますので，
\(K_{\rm{a}} = \large \frac{0.4}{0.6} \small [\rm{H}^+] = 2.0 × 10^{-5}\ \rm{mol/L}\)
\([\rm{H}^+] = 3.0 × 10^{-5}\ \rm{mol/L}\)
と求められます．

緩衝溶液（パターン3）

次は，塩基性のパターンについて考えていきましょう！
これが最後の問題です．

最後まで頑張りましょう！

\(0.1\ \rm{mol/L}\)の\(\rm{NH_3}\ 20\ \rm{mL}\)と\(0.1\ \rm{mol/L}\)の\(\rm{HCl}\ 10\ \rm{mL}\)の\([\rm{H}^+]\)は？
\(\rm{NH_3}\)の\(K_{\rm{b}} = 2.0 × 10^{-5}\ \rm{mol/L}\)

\(\rm{NH_3}\)に\(\rm{HCl}\)を加えると，以下のような反応が起こります．
NH₃　+　HCl　→　NH₄Cl

物質量変化を考えると，下のようになります．

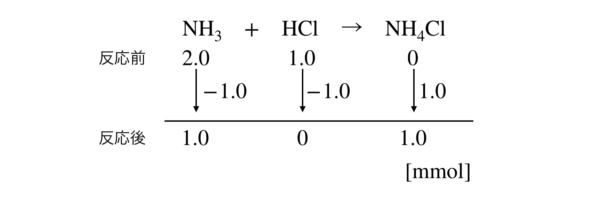
ここで，\(K_{\rm{b}}\)の式を確認してみましょう．
\(K_{\rm{b}}\)は以下の反応式の平衡定数です．
NH₃　+　H₂O　⇄　NH₄⁺　+　OH^–
これより，
\(K_{\rm{b}} = \large \frac{[\rm{NH_4^+}][\rm{OH}^-]}{[\rm{NH_3}]}\)
です．
この式にそれぞれの物質量（モル）を代入していきましょう．

\(K_{\rm{b}} = \large \frac{1.0}{1.0} \small [\rm{OH^-}] = 2.0 × 10^{-5}\)
\([\rm{OH^-}] = 2.0 × 10^{-5}\ \rm{mol/L}\)
となります．
\([\rm{H^+}] = \large \frac{K_{\rm{w}}}{[\rm{OH^-}]} \small = \large \frac{1.0 × 10^{-14}}{2.0 × 10^{-5}} \small = 5.0 × 10^{-10}\ \rm{mol/L}\)

本日は以上になります．