逆滴定（NH3編）

このような悩みをしっかりと解決していきます！
  

逆滴定の中でよく出てくる物質としてNH₃とCO₂があります．
今回はNH₃についてなぜ逆滴定をするのか，といった根本的な部分から説明していきます．
安心して最後までついてきてくださいね．
CO₂の逆滴定については次回解説していきます！
 
それでは今日も最後まで一緒に頑張りましょう！！
 
 

NH3の逆滴定（解説編）

まず，逆滴定についてお話ししていきましょう．

逆滴定とは，複数の酸・塩基を用いて中和滴定するということです．
複数の酸・塩基といってもイメージがわからないと思いますが，
最後まで読むと必ずわかるようになりますので，頑張っていきましょう．
 
 
まず，\(\rm{NH_3}\)の量を滴定しようとします．

しかし\(\rm{NH_3}\)は気体なので，そのままでは測定できません．
そこで水に吸収させて測定しようとする方もいるかもしれませんが，これには問題があります．
下の図のように，\(\rm{NH_3}\)は水に完全には溶解しないので，\(\rm{NH_3}\)が水から放出されてしまうのです．

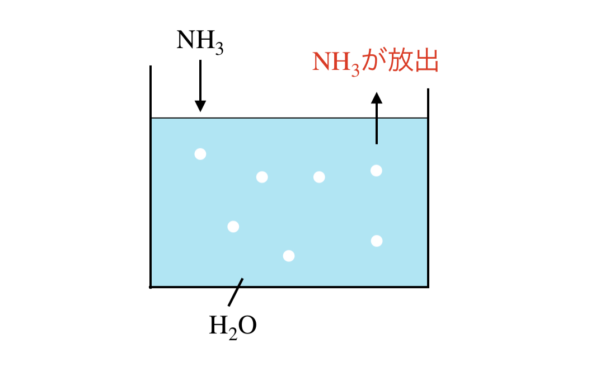
そのため\(\rm{NH_3}\)が完全に溶解する物質を使う必要があります．
これは強酸です！！
弱塩基の\(\rm{NH_3}\)を強酸と中和して吸収させるのです．

今回は強酸として\(\rm{HCl}\)を使用してみましょう！
\(\rm{HCl}\)は1価の酸で\(\rm{NH_3}\)と価数が等しいため，計算がラクです！
価数が異なるパターンについてもあとで練習しましょう．

この溶液の中には，過剰の\(\rm{HCl}\)が含まれています．

この溶液の中では以下のような反応が起こっています．

NH₃　+　HCl　→　NH₄Cl

この\(\rm{NH_4Cl}\)が溶液中から放出していかないので，
中和滴定を行うことで，\(\rm{NH_3}\)の量を正確に測定できるということです．
この場合は，\(\rm{NH_3 : NH_4Cl} = 1 : 1\)となっていますね！

この溶液には過剰の\(\rm{HCl}\)が含まれているので，下の図のようになりますね！
\(\rm{NH_3}\)と未反応の\(\rm{HCl}\)が残存しています．

この溶液は\(\rm{NH_4Cl+HCl}\)溶液になっています．
この溶液を強塩基である\(\rm{NaOH}\)で滴定することを考えていきましょう．

ここからは，どの物質が\(\rm{NaOH}\)と反応するかを見抜くことが非常に大切になります．
①溶液中に過剰に存在する\(\rm{HCl}\)との反応
HCl　+　NaOH　→　NaCl　+　H₂O
②溶液中に存在する\(\rm{NH_4Cl}\)との反応
NH₄Cl　+　NaOH　→　NaCl　+　NH₃　+　H₂O
③さらに加えていくと，\(\rm{NaOH}\)が過剰になっていきます．
これらを図にすると，下のようになります．

この反応について滴定曲線を描くと，下のようになります．

この滴定曲線で覚えておいてほしいことは，使用する\(\rm{pH}\)指示薬です．
図のように，メチルオレンジ（\(\rm{MO}\)）やメチルレッド（\(\rm{MR}\)）を使用します．
どちらの\(\rm{pH}\)指示薬を使用しても色の変化は赤→黄色となります．

\(\rm{pH}\)指示薬の色の変化がまだ覚えられていない方は，こちらの記事を参考にしてください！
中和滴定
すぐに覚えられますよ！
 
 
解説編は以上になります！
しっかりと理解して自分のものにしていってください．

NH3の逆滴定（実践編）

続いては，簡単な例題を解いて，理解したものを自分のものにしていきましょう！

（\(1\)）
硫酸アンモニウム\(\rm{(NH_4)_2SO_4}\)と水酸化ナトリウム\(\rm{NaOH}\)の反応式は必ず書けるようにして下さい．
テストで頻出ですよ！

(NH₄)₂SO₄ + 2NaOH → Na₂SO₄ + 2NH₃ + 2H₂O
 
 
 

（\(2\)）
この問題の全体像についてまず説明していきましょう．

（\(1\)）より\(\rm{(NH_4)_2SO_4}\)に\(\rm{NaOH}\)を加えて加熱することで，\(\rm{NH_3}\)が発生しますね．
そしてこの\(\rm{NH_3}\)を\(\rm{HCl}\)と中和反応したときに，\(\rm{HCl}\)が過剰であり，\(\rm{H^+}\)が残っている状態です．
残りの\(\rm{H^+}\)を中和するために最後に\(\rm{NaOH}\)を加えたということです．
いつものように図にすると，下のようになります．

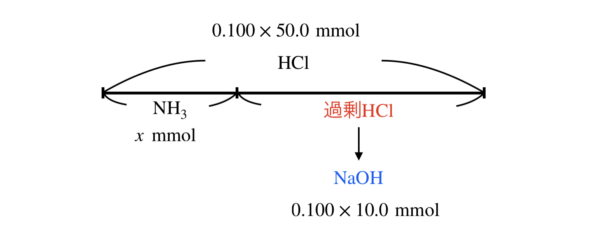
では，\(\rm{(NH_4)_2SO_4}\)の濃度を求めるために，発生した\(\rm{NH_3}\)のモルを求めていきましょう．
\(\rm{NH_3}\)を\(x\ \rm{mmol}\)とすると，中和点での\(\rm{H^+}\)のモル \(= \rm{OH^-}\)のモルとなるので，
\(0.100 × 50.0 = x + 0.100 × 10.0\)
\(x = 4.00\ \rm{mmol}\)
 

 
 
\(\rm{NH_3}\)のモルがわかれば，（\(1\)）の反応式に代入することで\(\rm{(NH_4)_2SO_4}\)のモルを求め，
最後に濃度を求めていきましょう．
\(\rm{(NH_4)_2SO_4}：\rm{NH_3} = 1：2\)なので，
\(\rm{(NH_4)_2SO_4}\)のモルは，\(4.00 × \large \frac{1}{2} \small = 2.00\ \rm{mmol}\)
\(20.0\ \rm{mL}\)に\(2.00\ \rm{mmol}\)が含まれているので，
\(\large \frac{2.00}{20.0} \small = 0.100\ \rm{mol/L}\)
となります．

では，今日はここまでです．
しっかりと復習して下さいね！！
 
 
次回は，CO₂の逆滴定について詳しく解説していきますね！