
初めて見たときは非常に難しく感じるかもしれません…
しかし,この記事を見ることで頭をスッキリとさせることができると思います!
今日も最後まで頑張りましょう!
物質の状態変化
物質の状態について考えるときには,\(p,V,T\)を考える必要があります.
その中でそれぞれを一定として考えると,以下の3パターンが考えられます.
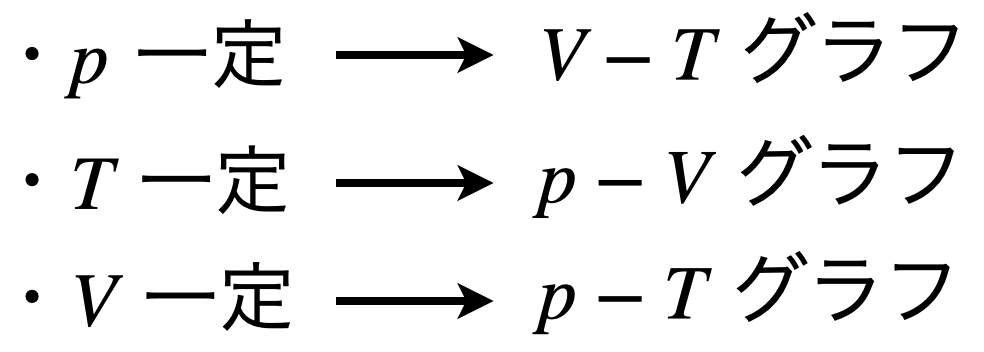
それぞれの条件におけるグラフを求められることもあるので,しっかりと考え,描けるようになっておきましょう!!
p一定におけるV-Tグラフ
\(p\)一定として,\(T\)を変化させたときの経路を状態図で確認してみましょう!
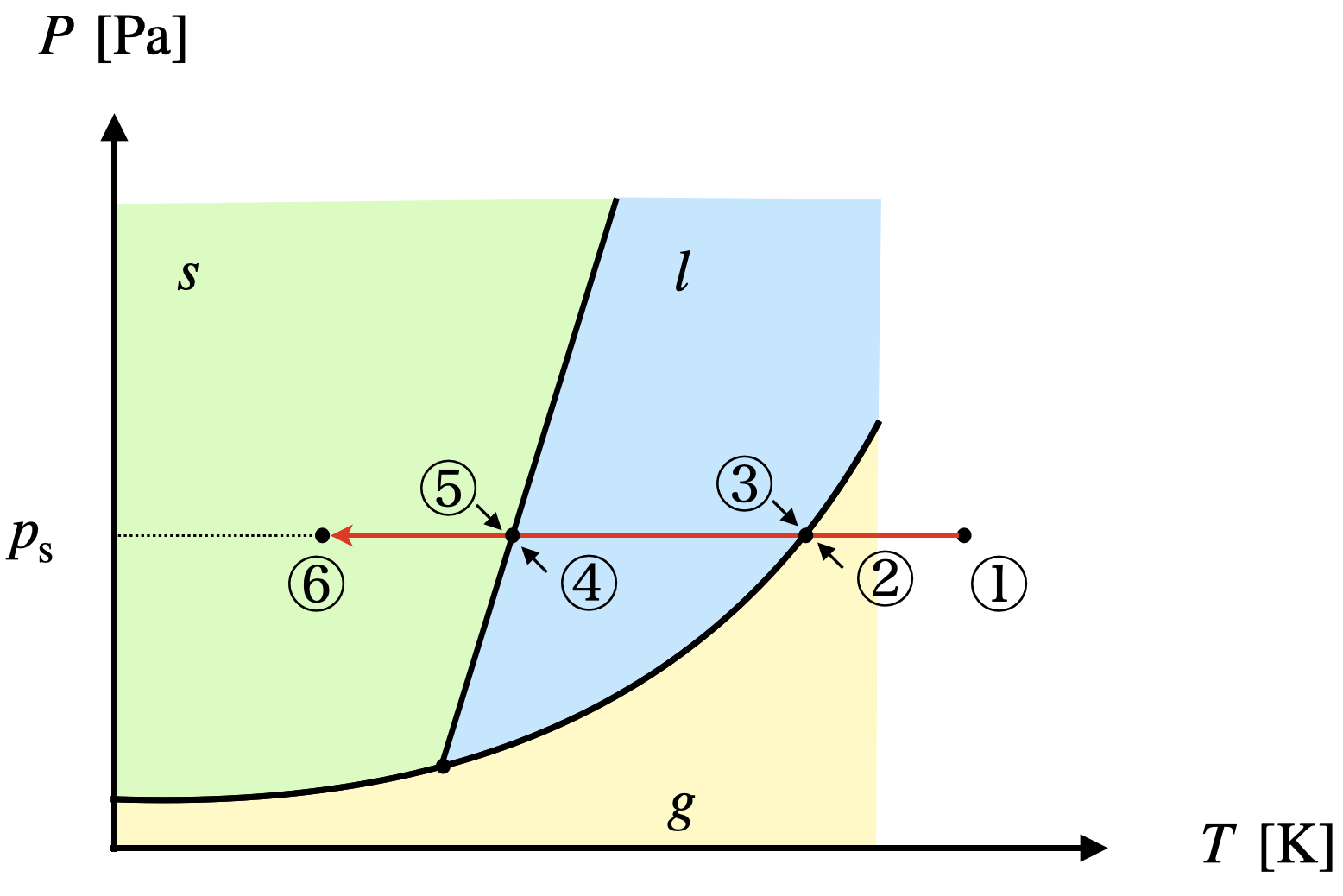
この図から,温度が①から⑥まで低下していることがわかります.
またそれぞれの状態についてみていきましょう.
①〜②:気体
②〜③:気液共存
③〜④:液体
④〜⑤:液固共存
⑤〜⑥:固体
次に体積について考えていきます.
①〜②:物質の状態が気体なので,状態方程式\(pV\ =\ nRT\)を使うことができます.
\(p,n\)一定となので,\(V\ =\ kT\)となります.
②〜③:気体が液体へと変化していきます.
ここで,一般に液体の体積は気体の体積と比較して,圧倒的に小さいので無視することができます.
つまり,容器内の物質がすべて液体になると,体積はほぼ0として考えることができるのです!
③〜⑥:この範囲においては,全て物質は液体なので,常に0となります.
以上より,\(V-T\)グラフを描くと下のようになります.
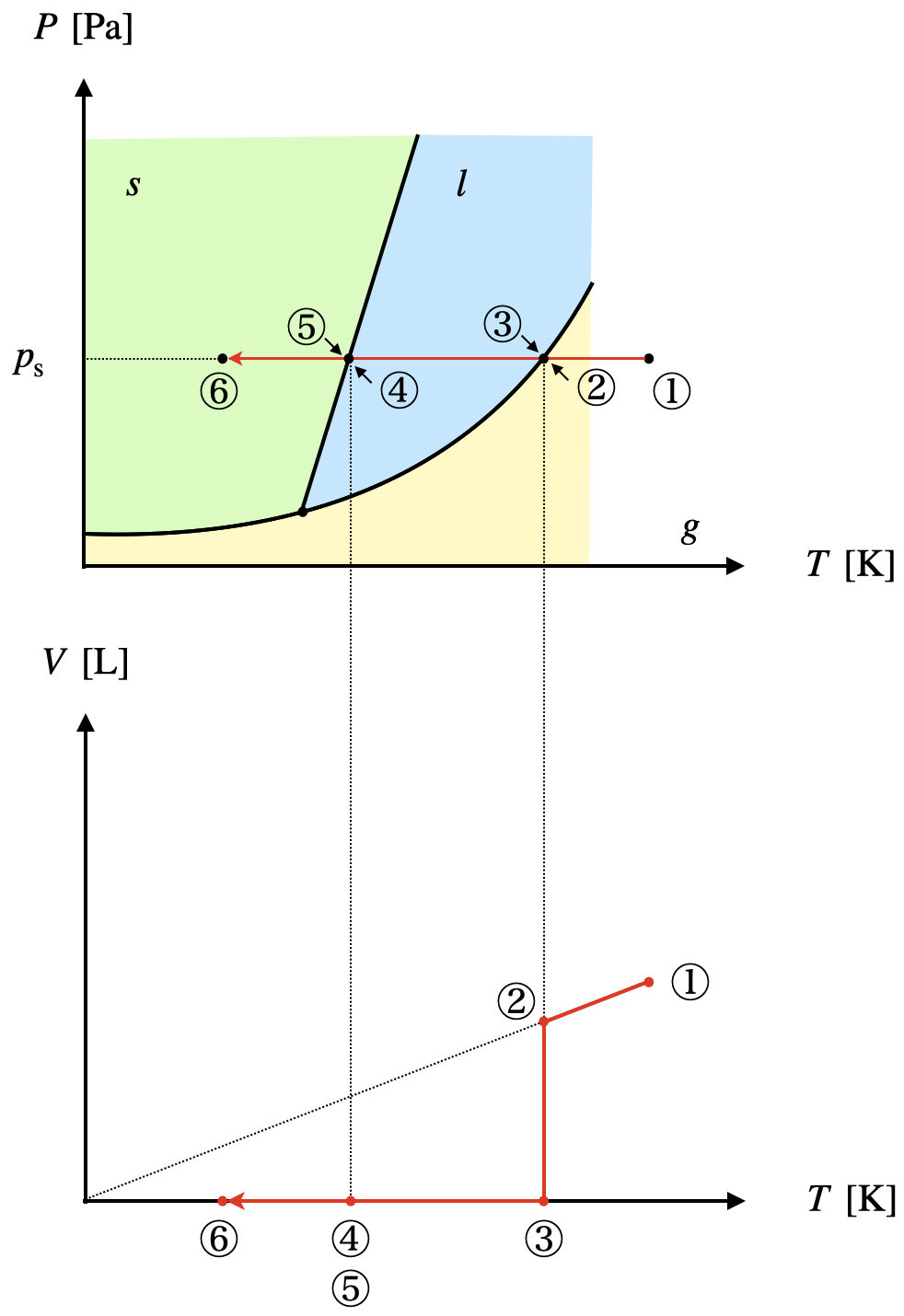
状態変化時の温度について注意するべき点があります.
それは,\(p\) 一定で\(T\)を下げていくと,気体から液体に変化しますが,そのときの温度は\(1\)点であるということです.
上のグラフで考えると,\(T_②\ =\ T_③\)の点です.
このとき,温度は変化していないことをしっかりと覚えてくださいね!
このグラフの形を覚えておくと,どこかで役に立つかもしれませんよ!
T一定におけるp-Vグラフ
\(T\)一定として,\(p\)を変化させたときの経路を状態図で確認してみましょう!
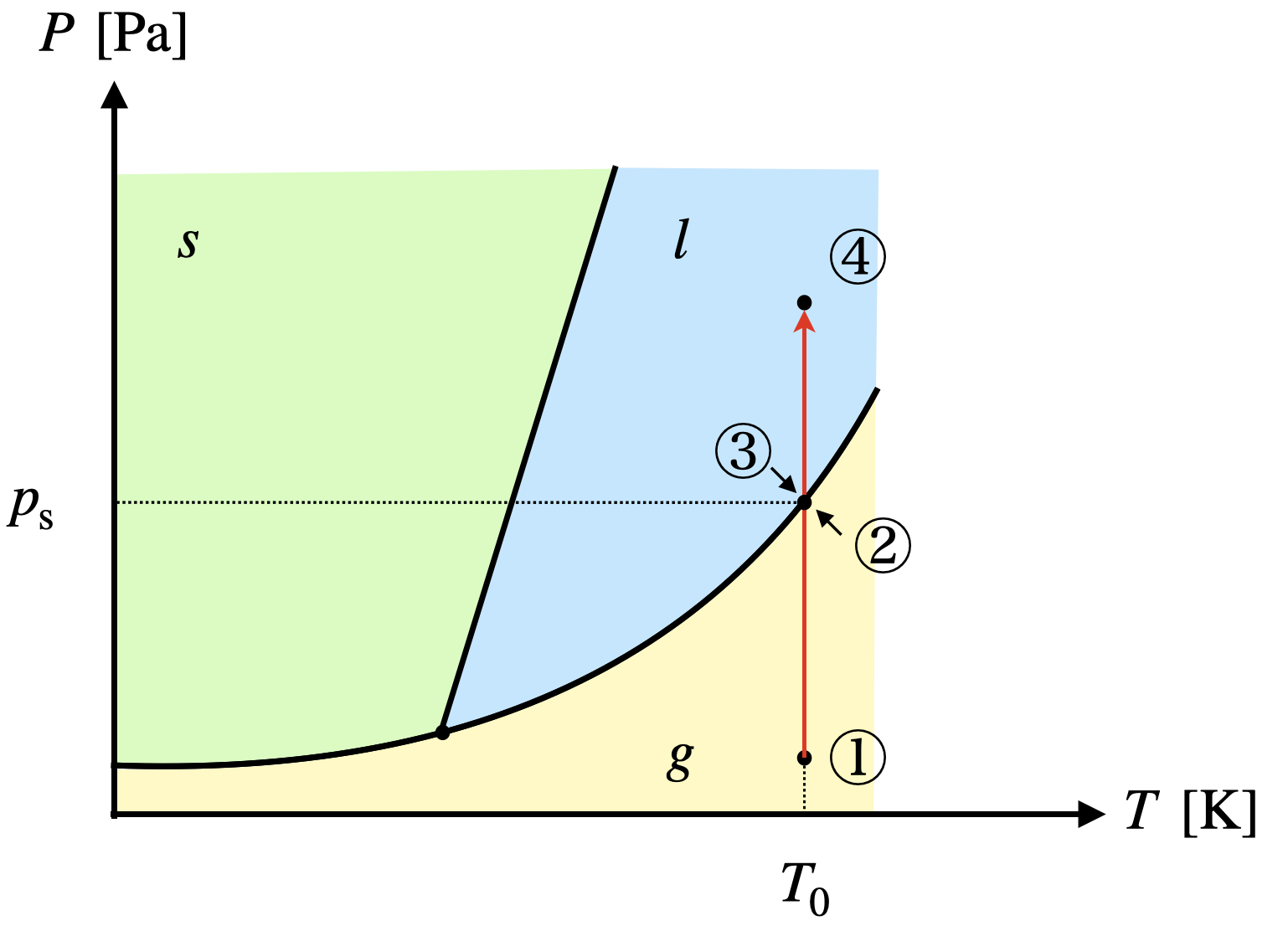
それぞれの状態をみていきましょう!
①〜②:気体
②=③:気液共存
③〜④:液体
次に,\(V\)(体積)について考えていきましょう!
①〜②:物質の状態が気体なので,先ほどと同様にして状態方程式\(pV\ =\ nRT\)を使うことができます.
\(n,T\)は一定なので,\(pV\ =\ k\)となり,反比例のグラフになります.
②〜③:液体が発生するので,体積は\(0\)へとむかいます.
③〜④:上でも説明したように,すべて液体なので体積は常に\(0\)となります.
以上をグラフにすると,以下のようになります.
ここでも液化はジワジワではなく,状態②・③の\(1\)点で起こります.
つまり「液化」が生じるときには,圧力は常に一定となっています.
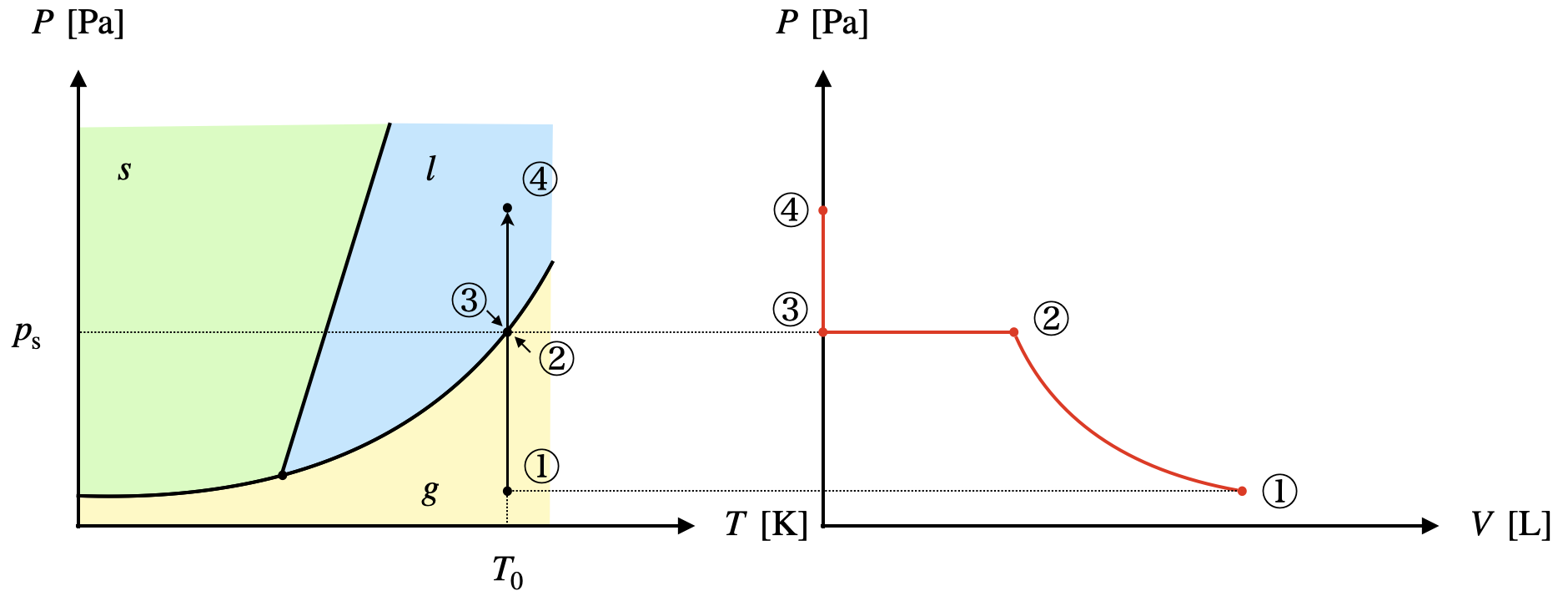
V一定におけるp-Tグラフ
今回も\(V\)一定としたときの変化について考えていきましょう.
ここで注意点があります.
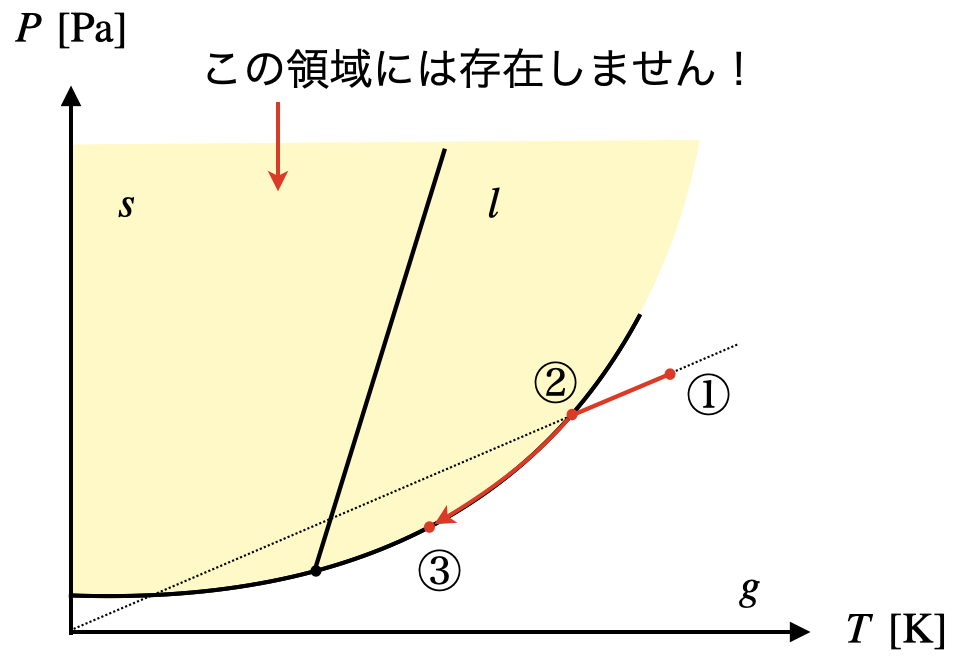
気体を体積一定の容器に入れて冷却し,液体や固体が生じたとしても,必ず気相が残るということです.
つまり,気液共存か気固共存となります.
これを状態図の中で考えると,
「\(V\)一定のときには,固体のみの領域,液体のみの領域は存在しない」ということです.
\(V\)一定のとき,圧力\(p\)を加えたときの様子を考えていきましょう.
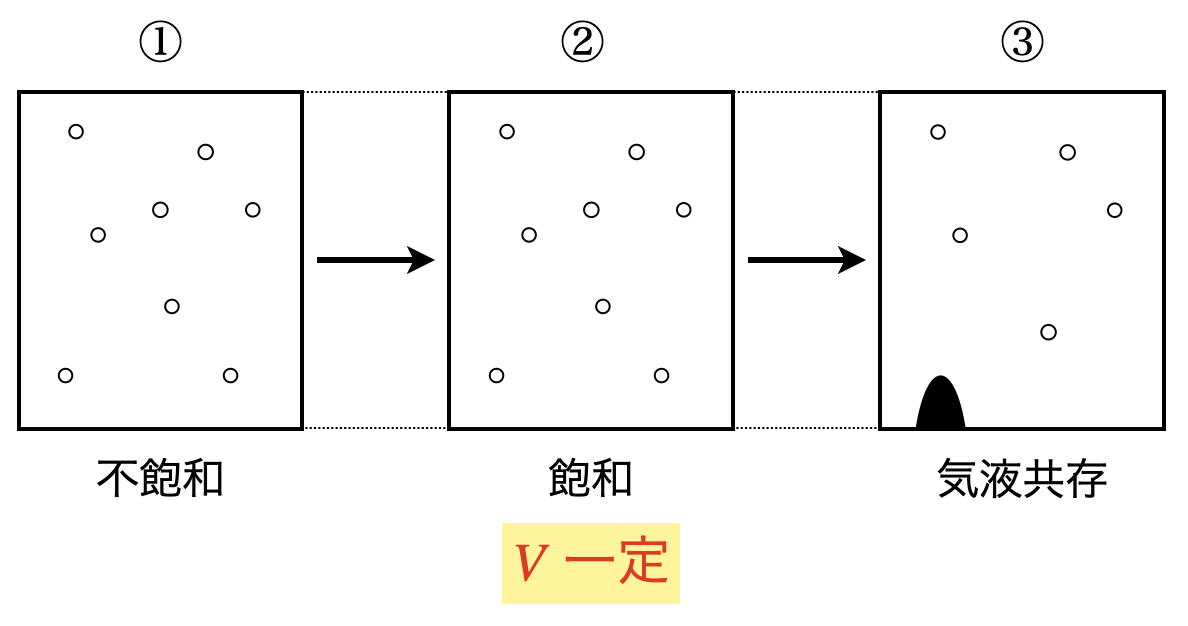
①〜②:容器内はすべて気体であり,このときは不飽和となっています..
\(n,V\)一定なので,\(p\ =\ kT\)となります.
②〜③:一部物質が液化しており,気液共存状態となっています.
容器内に液体が生じているので,容器内は飽和になっています.
これをグラフにすると,下のようになります.
②から③に変化するうちに,気液共存を保ちながらジワジワと液体が増加していき,圧力が減少していきます.
それぞれのグラフについてしっかりと描けるようにしておきましょう!
テストなどで求められることがありますよ!
状態変化の練習問題
それでは,練習問題を考えていきましょう!
今回の問題は少し難しいので,気合を入れて頑張りましょう!
メタノールの蒸気圧曲線がある.以下の問いに答えよ.
気体定数\(\ R\ =\ 8.3\ ×\ 10^3\ \rm{Pa\ L/mol\ K}\)とする.
(\(1\))ピストンつきの容器に\(\ 1.0\ \rm{mol}\)のメタノールを加え,\(1.0\ ×\ 10^5\ \rm{Pa}\)下で\(\ 40^\circ \rm{C}\)から\(\ 70^\circ \rm{C}\)まで加熱した.このときの\(V-T\)グラフは?
(\(2\))ピストンつきの容器に\(\ 1.0\ \rm{mol}\)のメタノールを加え,\(40^\circ \rm{C}\)で\(\ 1.0\ ×\ 10^5\ \rm{Pa}\)から\(\ 0.2\ ×\ 10^5\ \rm{Pa}\)まで変化させた.このときの\(p-V\)グラフは?
(\(3\))\(\ 1.0\ \rm{mol}\)のメタノールを\(\ 30\ \rm{L}\)の容器に加え,\(30^\circ \rm{C}\)から\(\ 70^\circ \rm{C}\)まで加熱した.このときの\(p-T\)グラフは?
(\(4\))\(\ 0.5\ \rm{mol}\)のメタノールと\(\ 0.5\ \rm{mol}\)の\(\ \rm{Ar}\)をピストンつきの容器に加えた.
①\(\ 1.0\ ×\ 10^5\ \rm{Pa}\)下でメタノールがすべて気体となるのは何\(^\circ \rm{C}\)以上か?
②\(\ 1.0\ ×\ 10^5\ \rm{Pa},40^\circ \rm{C}\)下で,メタノールの気体は何\(\rm{mol}\)か?また,容器の全体積はいくらか?
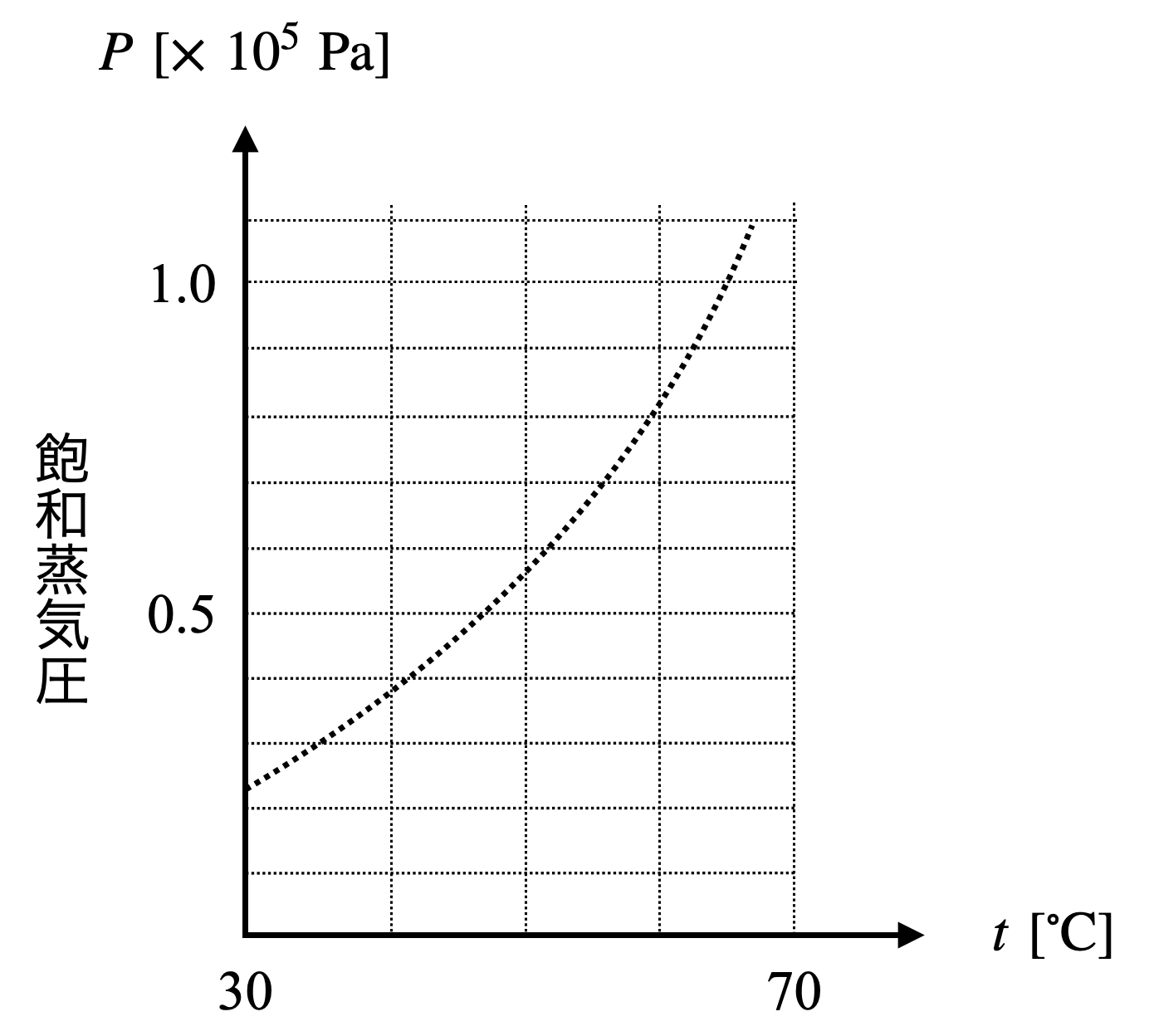
問題が多いですが,\(1\)つずつ解いていきましょう!まず問題に与えられている蒸気圧曲線は,状態図の気液境界線です.
(\(1\))
\(p\)一定で,\(T\)が変化しているため,\(1.0\ ×\ 10^5\ \rm{Pa}\)で\(\ 40^\circ \rm{C}\)から\(\ 70^\circ \rm{C}\)までの直線を書き込んでみましょう!
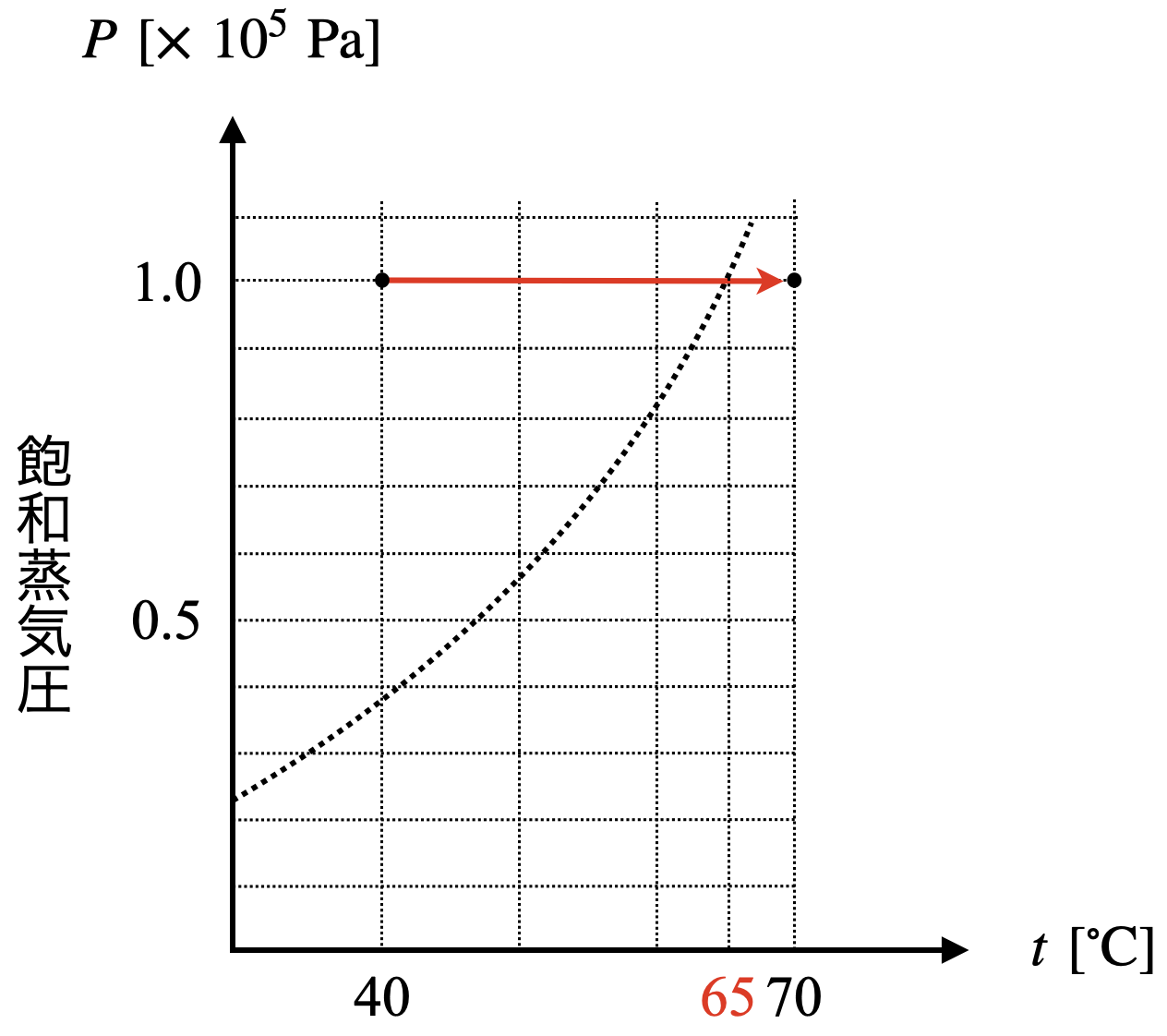
すると,約\(\ 65^\circ \rm{C}\)でこの直線と蒸気圧曲線が交わっていることがわかります.この点が気液共存状態となっており,液体から気体へとメタノールが状態変化しています.そのため,\(V-T\)グラフは以下のようになることがわかります.
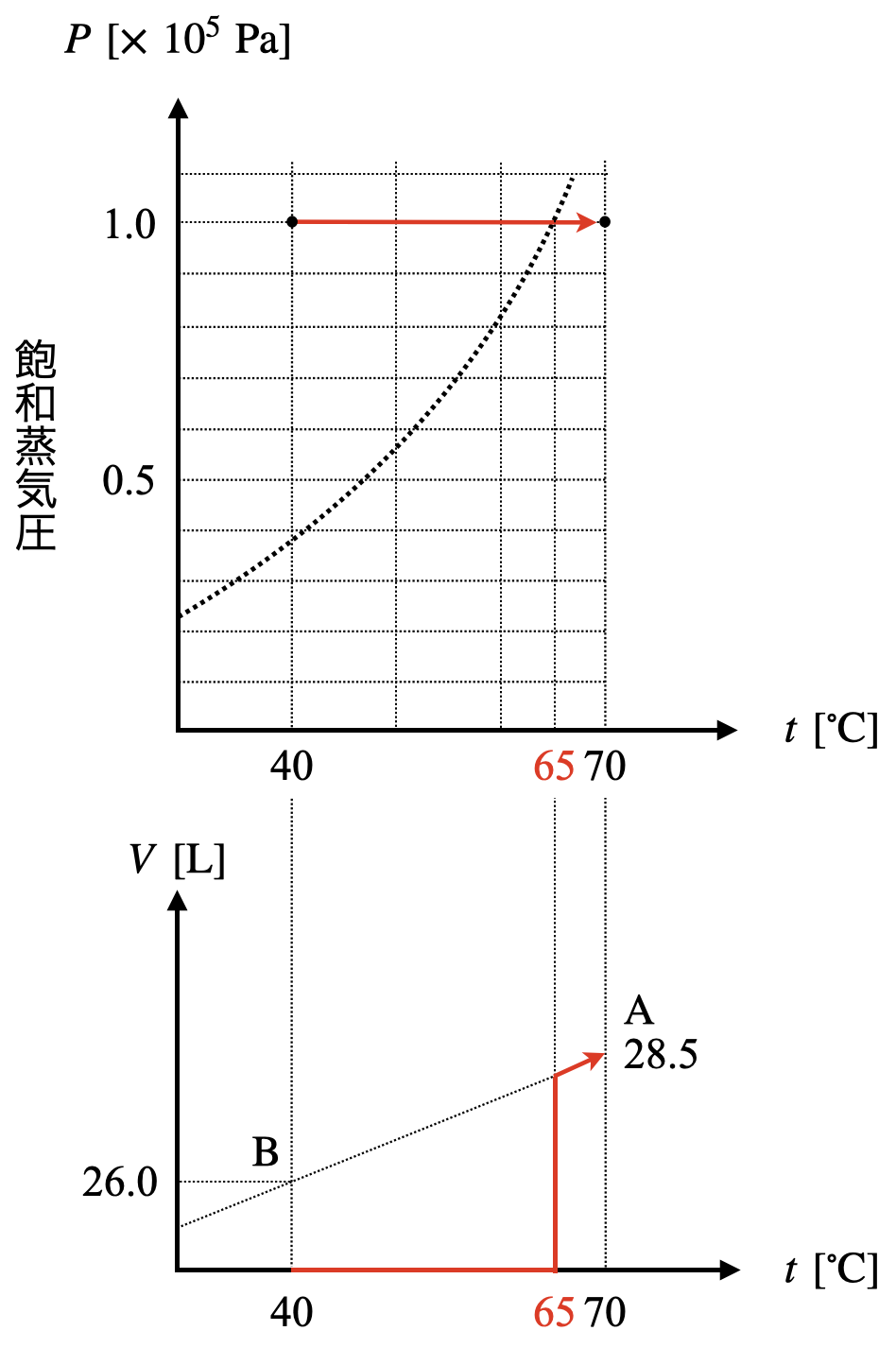
最後に,直線\(\rm{AB}\)を引く方法について解説していきます.
\(\ 40^\circ \rm{C}\)のとき,すべて気体であると仮定したときの圧力は以下のようになります.
\(V\ =\ \large \frac{nRT}{p}\ \small =\ \large \frac{1.0\ ×\ 8.3\ ×\ (273\ +\ 40)}{100}\ \small =\ 26.0\ \rm{L}\)
次に,\(\ 70^\circ \rm{C}\)での気体の体積を求めてみましょう!
\(\ 70^\circ \rm{C}\)ではすべて気体なので,
\(V\ =\ \large \frac{nRT}{p}\ \small =\ \large \frac{1.0\ ×\ 8.3\ ×\ (273\ +\ 70)}{100}\ \small =\ 28.5\ \rm{L}\)
となります.
この\(2\)点を結ぶ直線を引くことで,\(V-T\)グラフを完成させることができます!
(\(2\))
\(T\)一定で,\(p\)が変化しています.そのときの体積変化の様子をグラフに描いてみましょう!
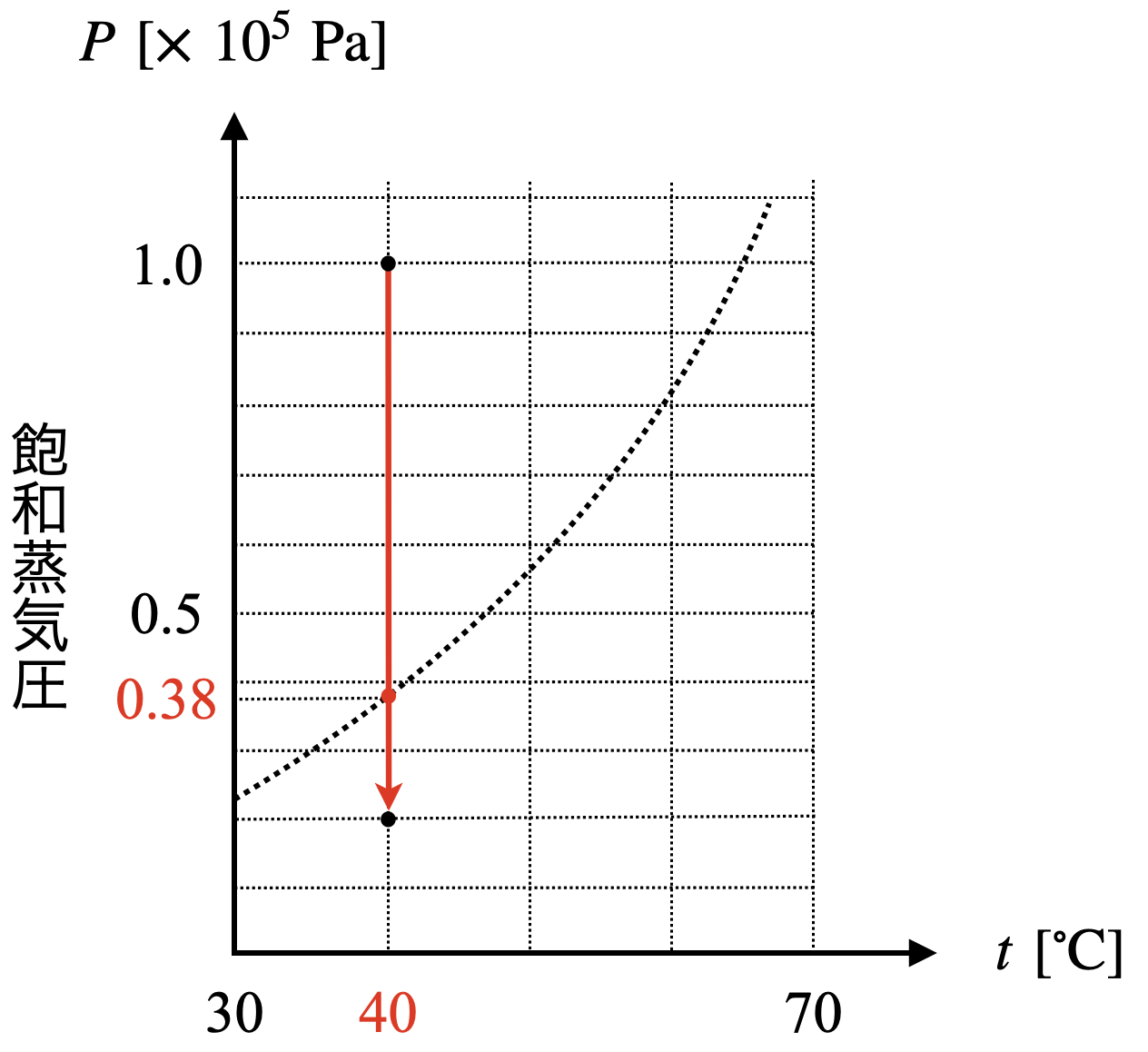
グラフから\(\ 40^\circ \rm{C}\)での飽和蒸気圧は約\(\ 38\ \rm{kPa}\)であるとわかります.
ここから場合分けをして考えていきましょう!
・\(\ p\ >\ 38\ \rm{kPa}\)のとき,
物質は液体なので,体積は\(\ 0\)となります.
・\(\ p\ <\ 38\ \rm{kPa}\)のとき,
物質は気体なので,状態方程式\(\ pV\ =\ nRT\)を使うことができます.
それぞれの体積\(V\)を求めていきましょう!
\(38\ \rm{kPa}\)のとき,
\(V\ =\ \large \frac{nRT}{p}\ \small =\ \large \frac{1\ ×\ 8.3\ ×\ (273\ +\ 40)}{38}\ \small =\ 68.4\ \rm{L}\)
\(20 \ \rm{kPa}\)のとき,
\(V\ =\ \large \frac{1\ ×\ 8.3\ ×\ (273\ +\ 40)}{20}\ \small =\ 130\ \rm{L}\)
となります.
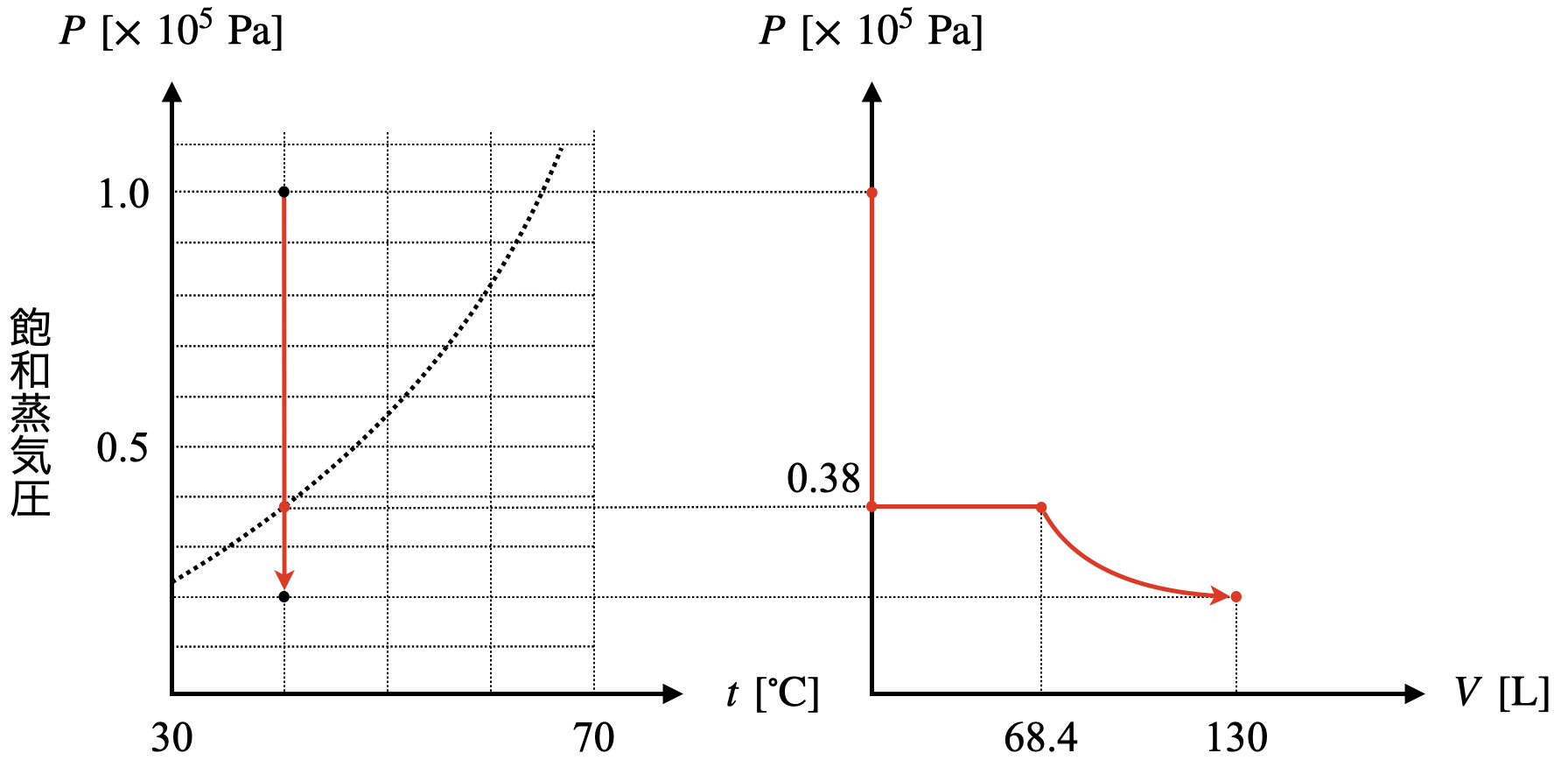
(\(3\))
\(V\)一定で,\(T\)を変化させたときの様子をグラフで描いてみましょう!
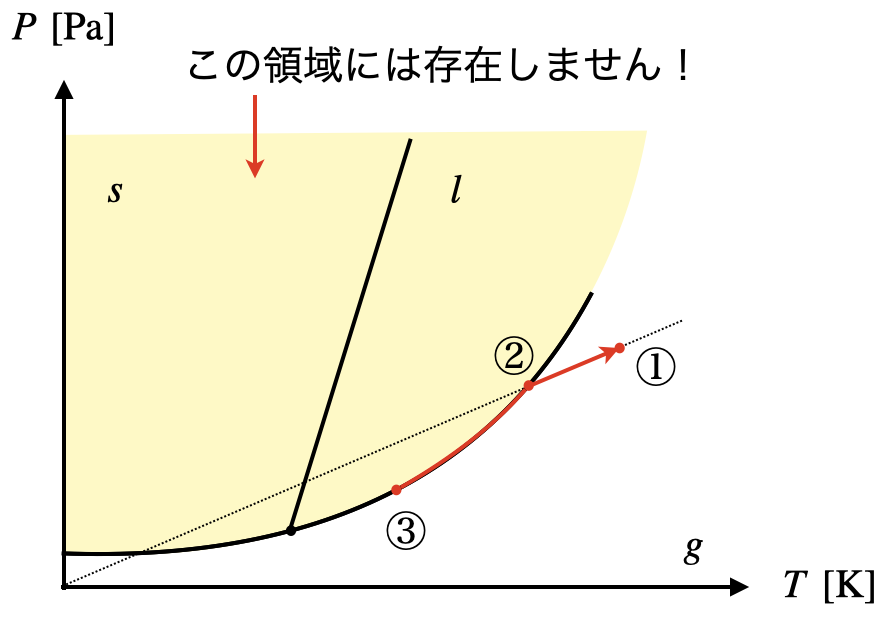
それぞれの温度における圧力を求めていきましょう!
・\(t\ =\ 30^\circ \rm{C}\)のとき,
\(p\ =\ \large \frac{1.0\ ×\ 8.3\ ×\ (273\ +\ 30)}{40}\ \small =\ 62.8\ \rm{kPa}\)
・\(t\ =\ 70^\circ \rm{C}\)のとき,
\(p\ =\ \large \frac{1.0\ ×\ 8.3\ ×\ (273\ +\ 70)}{40}\ \small =\ 71.2\ \rm{kPa}\)
そして図より直線\(\rm{AB}\)と蒸気圧曲線の交点の温度は約\(\ 55^\circ \rm{C}\)であることがわかります.
以上より,下のようなグラフを描くことができます!

(\(4\))
①\(メタノール:\rm{Ar}\ =\ 0.5\ \rm{mol}:\ 0.5\ \rm{mol}=\ 1:1\)の割合で混合されているので,この比を用いることでそれぞれの気体の分圧を求めることができます.
\(p_{メタノール}\ =\ p_{\rm{Ar}}\ =\ 100\ ×\ \large \frac{1}{2}\ \small =\ 50\ \rm{kPa}\)
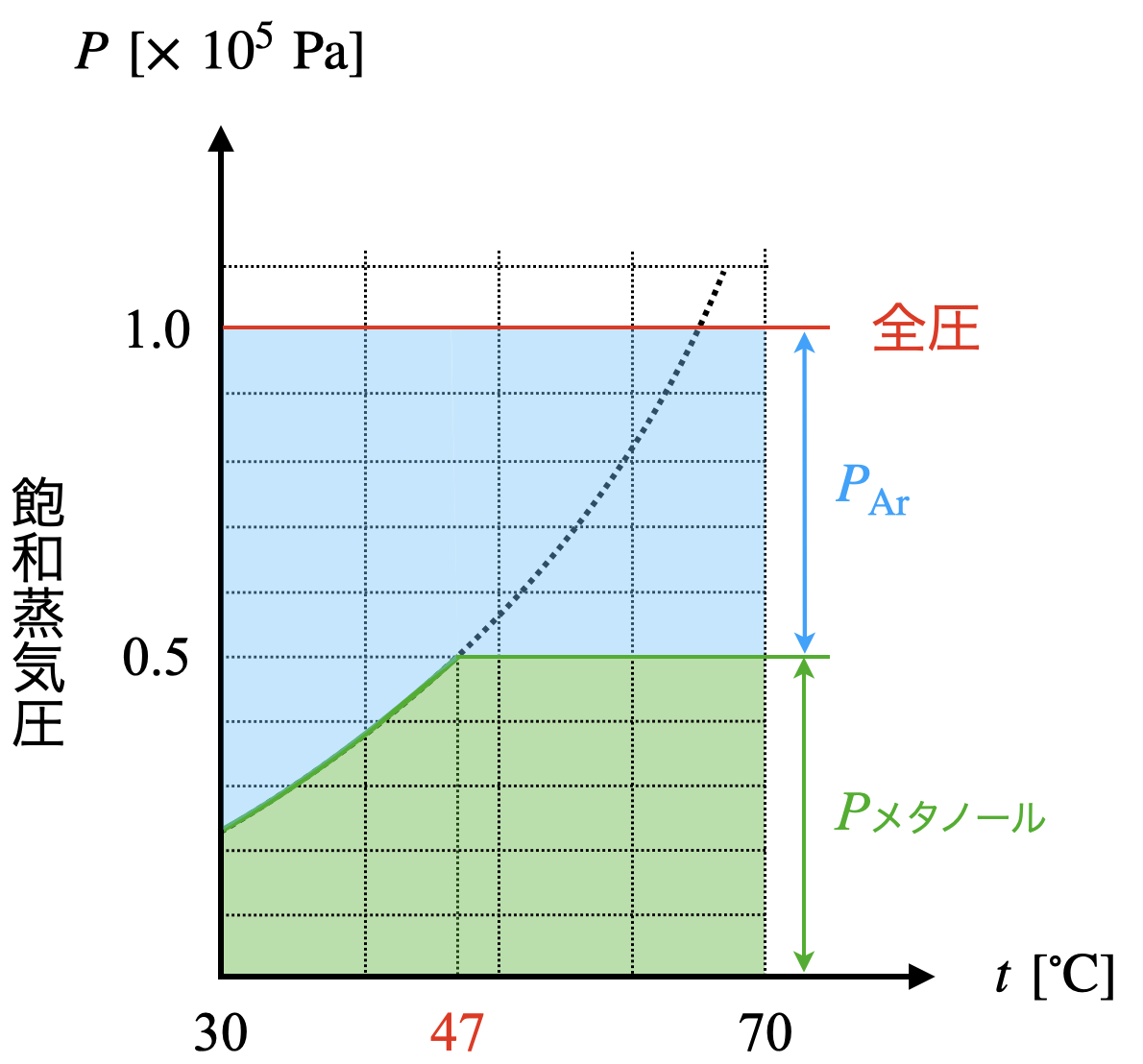
図より,メタノールの飽和蒸気圧が\(\ 50\ \rm{kPa}\)となるのは,約\(\ 47^\circ \rm{C}\)であるということがわかります.
②メタノールの\(\ 40^\circ \rm{C}\)での飽和蒸気圧は約\(\ 38\ \rm{kPa}\)となります.そのため,圧力についてメタノール:\(\rm{Ar}\ =\ 38\:\ 62\)となります.
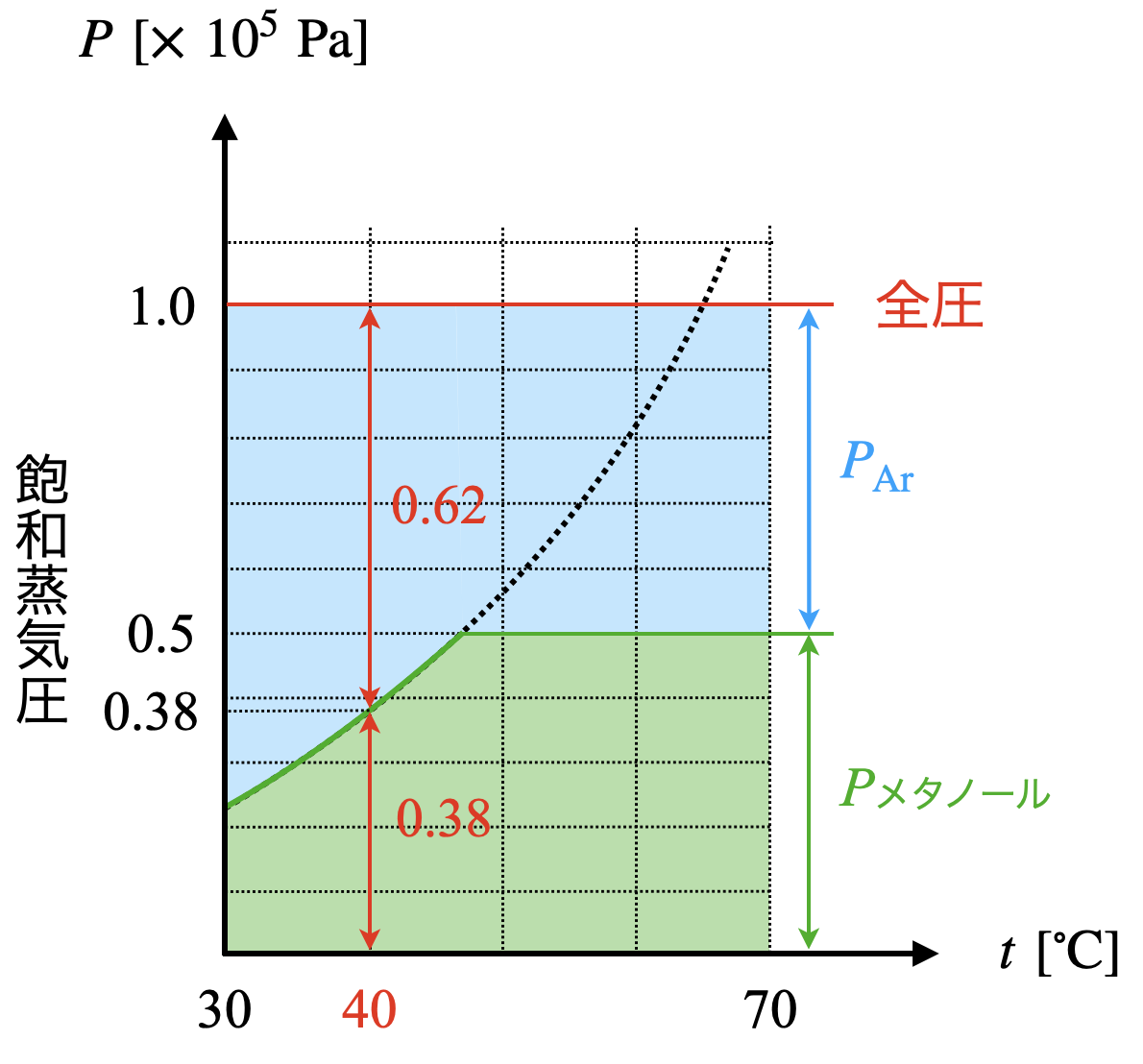
ここで,\(V,T\)一定なので,\(n\ =\ kp\)となります.つまり,圧力の比を考えることで,モルの比を考えることができるということです.
そのため,
\(n_{\rm{Ar}}\ ×\ \large \frac{38}{62}\ \small =\ 0.5\ \large \frac{38}{62}\ \small =\ 0.31\ \rm{mol}\)
またそのときの体積\(\ V\)は,すべて気体である\(\rm{Ar}\)に対して状態方程式\(pV\ =\ nRT\)を適用することで求めることができます.
\(V\ =\ \large \frac{0.5\ ×\ 8.3\ ×\ (273\ +\ 40)}{62}\ \small =\ 21.0\ \rm{L}\)
今回は以上となります!
今回も練習問題はかなり難しかったと思いますが,何度も復習すると必ずできるようになります!
この問題を使って,自分のものにしてくださいね!



コメント