
混合気体については,条件によってはモルを考えなくても解ける問題が多くあります!
その考え方や解き方などについて必ず理解できますよ!
それでは,今日も頑張っていきましょう!!
\(\rm{You Tube}\)ではより具体的な問題を解説しているので,ぜひそちらもご覧ください!
混合気体
混合気体の問題を考えるときは,仮想的に分けることが非常に重要になります.
種類ごとに分けるときに大切なのが,分体積と分圧という考え方です.
それぞれの考え方について,順に説明していきましょう.
分体積
分体積とは,気体が混合している状態で\(p,T\)一定の条件で種類ごとに分けた体積のことをいいます.
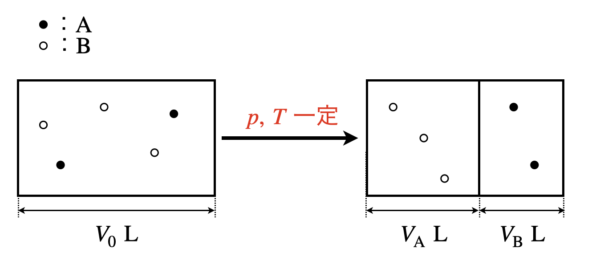
分体積を考えるときに重要な式が2つあります.
①\(\ V_0\ =\ V_{\rm{A}}\ +\ V_{\rm{B}}\)
②\(\ \large \frac{V_{\rm{A}}}{V_{\rm{B}}}\ \small =\ \large \frac{n_{\rm{A}}}{n_{\rm{B}}}\)
〈\(proof\)〉
①\(\ V_0 = \large \frac{(n_{\rm{A}}\ +\ n_{\rm{B}})RT_0}{P_0}\ \small =\ \large \frac{n_{\rm{A}}RT_0}{P_0}\ \small +\ \large \frac{n_{\rm{B}}RT_0}{P_0}\ \small =\ V_{\rm{A}}\ +\ V_{\rm{B}}\)
②\(\ \large \frac{V_{\rm{A}}}{V_{\rm{B}}}\ \small =\ \large \frac{\frac{n_{\rm{A}}RT_0}{P_0}}{\frac{n_{\rm{B}}RT_0}{P_0}}\ \small =\ \large \frac{n_{\rm{A}}}{n_{\rm{B}}}\)
このポイントを必ず覚えておいてください!!
分圧
分圧とは,気体が混合している状態で\(V,T\)一定の条件で種類ごとに分けた圧力のことをいいます.
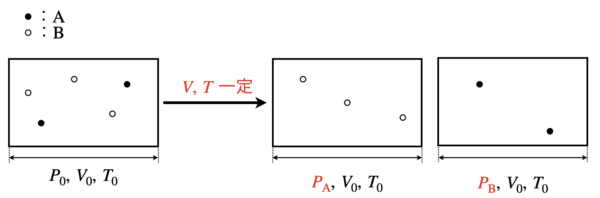
分圧を考えるときに重要な式が3つあります.
①\(\ P_0\ =\ P_{\rm{A}}\ +\ P_{\rm{B}}\)
②\(\ \large \frac{P_{\rm{A}}}{P_{\rm{B}}}\ \small =\ \large \frac{n_{\rm{A}}}{n_{\rm{B}}}\)
③\(\ P_{\rm{A}}\ =\ \large \frac{n_{\rm{A}}}{n_{\rm{A}}\ +\ n_{\rm{B}}}\ \small P_0\ =\ \)\(x_{\rm{A}}\)\(P_0 \) \(\ \left(x_{\rm{A}}\ =\ \large \frac{n_{\rm{A}}}{n_{\rm{A}}\ +\ n_{\rm{B}}} \right) \)
ここで,\(x_{\rm{A}}\)は\(\rm{A}\)のモル分率を表しています.
〈\(proof\)〉
①\(\ P_0\ =\ \large \frac{(n_{\rm{A}}\ +\ n_{\rm{B}})RT_0}{V_0}\ \small =\ \large \frac{n_{\rm{A}}RT_0}{V_0}\ \small +\ \large \frac{n_{\rm{B}}RT_0}{V_0}\ \small =\ P_{\rm{A}}\ +\ P_{\rm{B}}\)
②\(\ \large \frac{P_{\rm{A}}}{P_{\rm{B}}}\ \small =\ \large \frac{\frac{n_{\rm{A}}RT_0}{V_0}}{\frac{n_{\rm{B}}RT_0}{V_0}}\ \small =\ \large \frac{n_{\rm{A}}}{n_{\rm{B}}}\)
③\(\ P_{\rm{A}}\ =\ \large \frac{n_{\rm{A}}RT_0}{V_0}\ \small =\ \large \frac{n_{\rm{A}}}{n_{\rm{A}}\ +\ n_{\rm{B}}} \cdot \frac{(n_{\rm{A}}\ +\ n_{\rm{B}})RT_0}{V_0}\ \small =\ \large \frac{n_{\rm{A}}}{n_{\rm{A}}\ +\ n_{\rm{B}}} \small P_0\ =\ x_{\rm{A}}P_0\)
モル分率については,今後もよく出てくるので,しっかりと覚えてくださいね!
\(x_{\rm{A}}\)は全体に占める成分\(\rm{A}\)の割合を表しています.
以上より,以下のポイントをしっかりと覚えてください!
\(p,T\)一定 → 分体積
\(n,T\)一定 → 分圧
混合気体の練習問題
それでは練習問題を使いながら,慣れていきましょう!
(\(1\))\(\rm{C_2H_4}\)(エチレン)\(5.0\ \rm{L}\)と\(\rm{H_2}\)を\(2.0\ \rm{L}\)で付加反応をさせた.
反応前後で圧力,温度を変えない条件で,反応後の混合気体の体積を求めよ.
(\(2\))\(\rm{C_2H_4}\)(エチレン)\(5.0\ ×\ 10^5\ \rm{Pa}\)と\(\rm{H_2}\)を\(2.0\ ×\ 10^5\ \rm{Pa}\)で付加反応をさせた.
反応前後で体積,温度を変えない条件で,反応後の混合気体の体積を求めよ.
(\(1\))
まず反応式は以下のようになります.
\(\rm{C_2H_4\ +\ H_2\ →\ C_2H_6}\)
本問題では\(p,T\)一定なので,\(pV\ =\ nRT\)で考えると,\(V\ =\ kn\)となります.
つまり,モルの代わりに分体積で考えることができるということです!
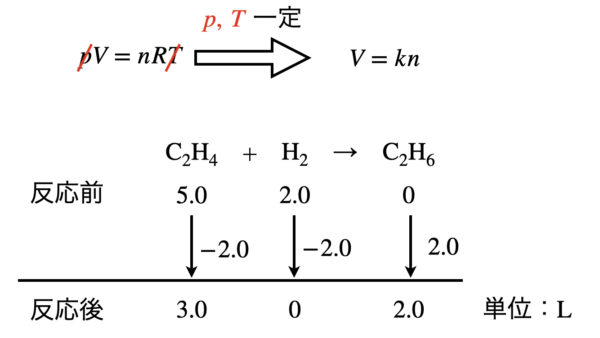
これから混合気体の体積は,\(5.0\ \rm{L}\)となります.
(\(2\))
本問題は,\(V,T\)一定なので,\(pV\ =\ nRT\)で考えると,\(p\ =\ kn\)となります.
つまり,モルの代わりに分圧で考えることができます.
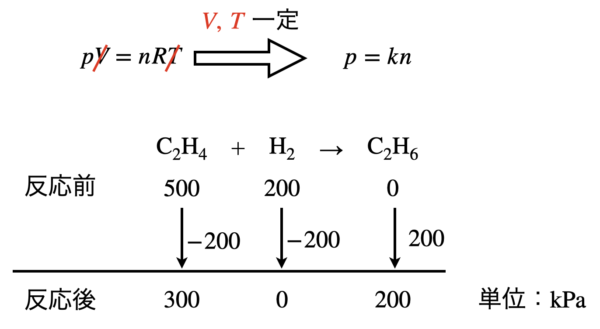
これより混合気体の圧力は,\(500\ \rm{kPa}\)となります.



コメント