
飽和蒸気圧については,今解いている問題が状態図のどこにいるのかを理解することが非常に重要になります!
今日も基礎からわかりやすく解説していきますよ!
それでは,今日も頑張っていきましょう!!
解説してほしい分野があればぜひ次の記事のコメント欄で教えてくださいね!

\(\rm{You Tube}\)ではより具体的な問題を解説しているので,ぜひそちらもご覧ください!
飽和蒸気圧
密閉空間内において,液体が蒸発できる圧力には限界があり,この限界圧力を飽和蒸気圧といいます.
液体が蒸発できる限界を物質量(モル)で考えないことには,理由があります.
それは液体が蒸発できる限界値は,密閉容器の体積に関係なく一定であるからです.
つまり下の図のように,容器の中の物質量(モル)に関係なく,圧力は一定になるということです.
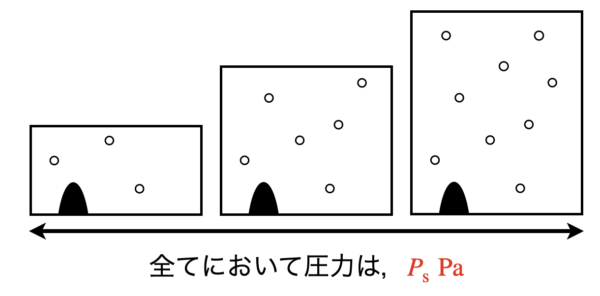
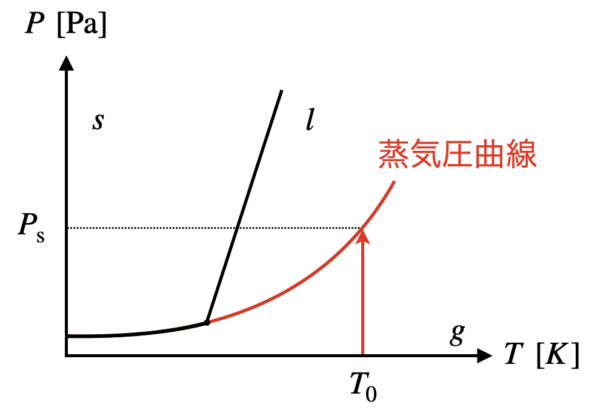
飽和蒸気圧を状態図で表すと,次のようになります.
ある温度と蒸気圧曲線の交点が飽和蒸気圧ということになります.
飽和蒸気圧とその状態
密閉容器中に存在する液体が全て蒸発できるかどうかを判定するためには,液体が全て蒸発したと仮定したときの圧力(\(p_{\rm{if}}\))と飽和蒸気圧(\(p_{\rm{s}}\):飽和(\(\rm{saturated}\)の\(\rm{s}\)))の大小を比較する必要があります.
では,それぞれの状態に区別して考えていきましょう.
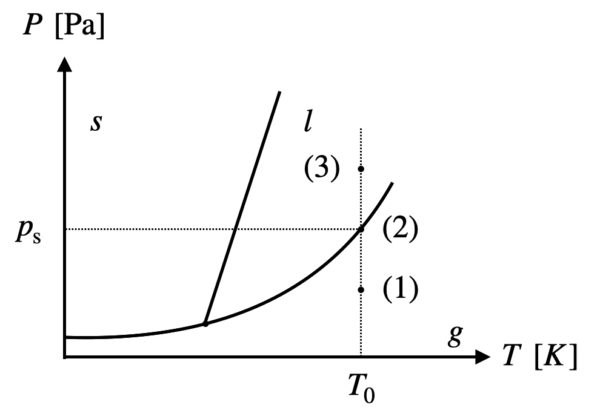
(1)のとき
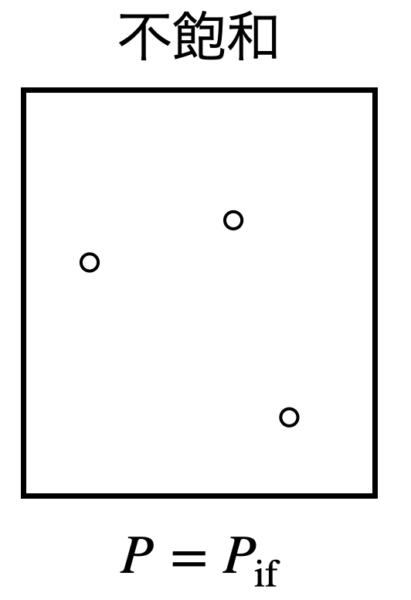
(\(1\))のとき,\(p_{\rm{if}}\ <\ p_{\rm{s}}\)となっています.
この場合は,状態図より物質は気体の領域にいます.
そのため容器中の物質は蒸発して全て気体となっており,まだまだ蒸発することができるので,不飽和となっています.
このときの容器内の圧力は\(pV=nRT\)で求めた\(p_{\rm{if}}\)となります.
(2)のとき
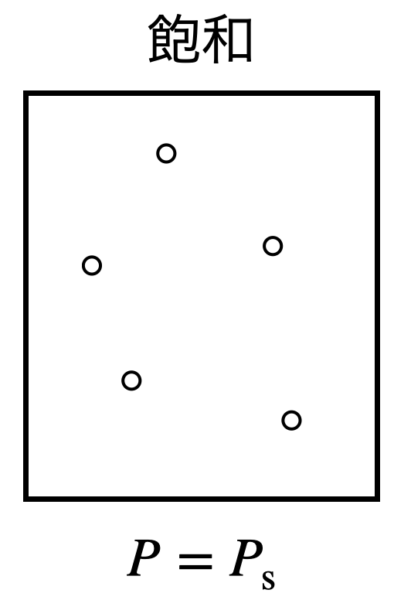
(\(2\))のとき,\(p_{\rm{if}}\ =\ p_{\rm{s}}\)となっています.
状態図より,液体は境界線ギリギリで全て蒸発し,気体になっていることが分かります.
そのため容器内は飽和となっていて,容器内の圧力は\(p_{\rm{s}}\)となります.
(3)のとき
(\(3\))のとき,\(p_{\rm{if}}\ >\ p_{\rm{s}}\)となっています.
仮定して求めた圧力が飽和蒸気圧よりも大きいときは,液体が蒸発できる空間が容器内にあるかどうかに着目して考える必要があります.
①容器内に液体が蒸発する空間があるとき
頑丈な容器などによって,気体がさらに蒸発できる空間が存在するときは,飽和していることが分かります.
また限界を越している分については液体へと変化しており,気液共存状態になっています.
そのため,容器内の圧力は飽和蒸気圧\(p_{\rm{s}}\)となります.
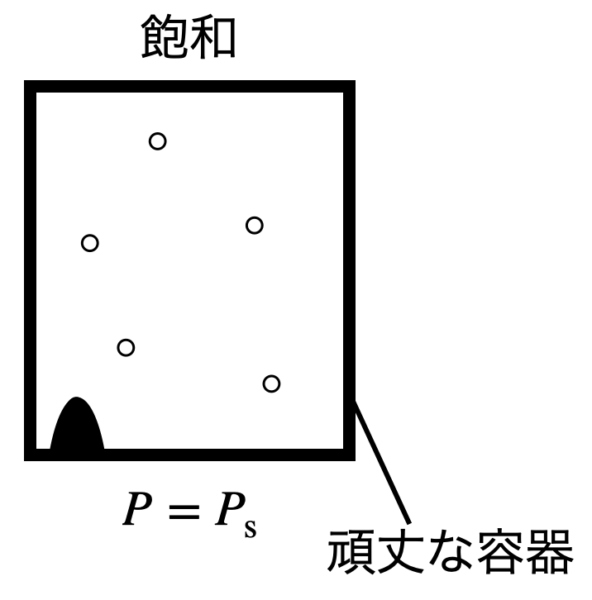
容器内の全物質量を\(n_0\ \rm{mol}\),飽和蒸気圧を\(p_{\rm{s}}\ \rm{kPa}\)として液体として残った物質量\(n_{\rm{l}}\ \rm{mol}\)を求めてみましょう.
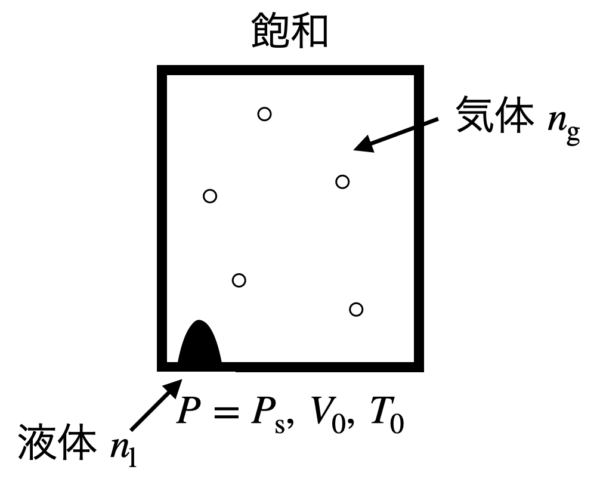
まずは,\(pV=nRT\)から気体になった物質量\(n_{\rm{g}}\ \rm{mol}\)を求めていきます.
圧力として\(p=p_{\rm{s}}\)を用いると,\(n_{\rm{g}}\ =\ \large \frac{p_{\rm{s}}V_0}{RT_0}\)
そのため,\(n_{\rm{l}}\)は\(n_0\)から\(n_{\rm{g}}\)を引くことで求めることができます.
\(n_{\rm{l}}\ =\ n_0\ -\ n_{\rm{g}}\ =\ n_0\ -\ \large \frac{p_{\rm{s}}V_0}{RT_0}\)
液体の体積は非常に小さいので,気体の体積を求めるときは無視してOKです!
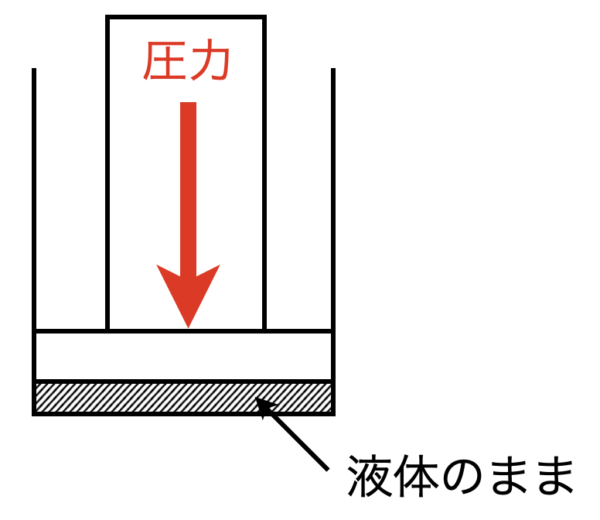
②容器内に液体が蒸発する空間がないとき
気体をピストンなどで押すと,容器が液体のみとなり,蒸発できる空間はなくなります.
この場合は,\(p_0\ \rm{kPa}\)となります.
混合気体と蒸気圧の混合問題の捉え方
混合気体の問題の中で,蒸気圧を考慮しなければならないときは,必ず分圧の問題と捉えてください!
そのため,すぐに\(V,T\)一定として図を描いてください!
\(A,B\)の物質が混合されて容器内に含まれているときは,先ほども説明したように\(A\)と\(B\)をそれぞれ別々に考え,液体\(B\)が,蒸発すると考えていきます.
この場合,先ほどと同様に,\(3\)パターンが考えられます.

(1)のとき
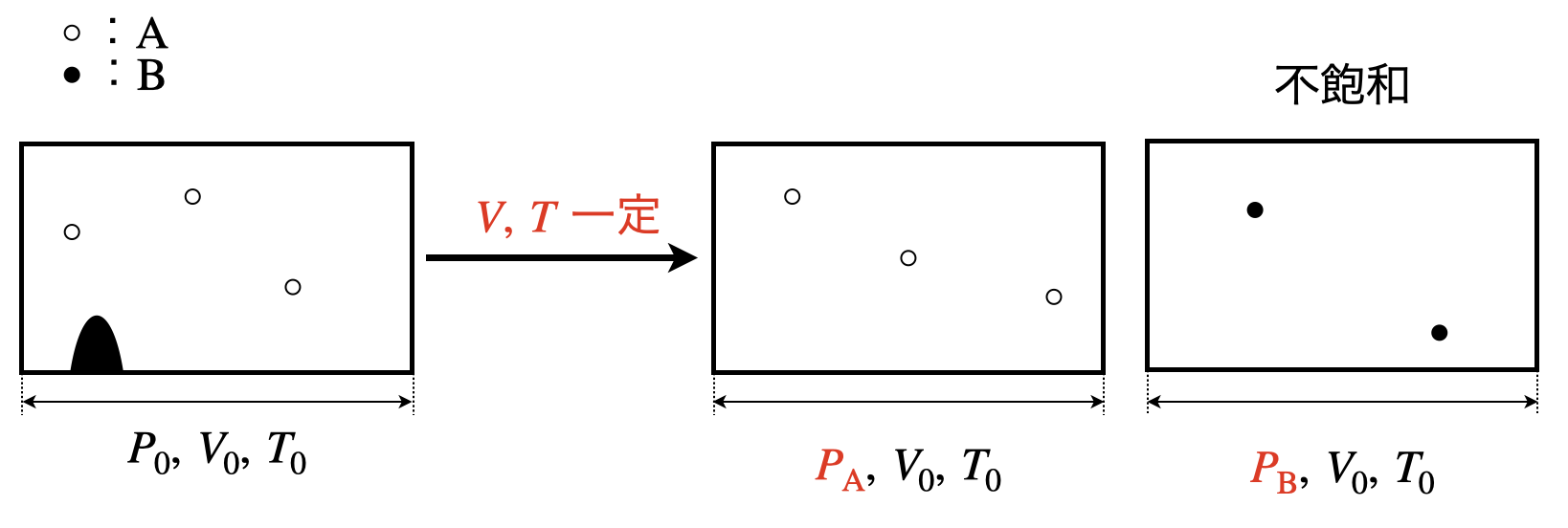
(\(1\))のとき,\(p_{\rm{B}}\ >\ p_{\rm{sB}}\)となっています.
この場合は,状態図より\(B\)は気体の領域にいます.
容器中の物質は蒸発して全て気体となっており,不飽和となっています.
そのため,容器内の\(B\)の圧力は\(p_{\rm{B}}\)となります.
また,物質\(A\)は物質\(B\)に関係なく,\(p_{\rm{A}}\)となります.
今後も物質\(A\)の圧力は常に\(p_{\rm{A}}\)となります.
そのため,全圧は\(p_{\rm{A}}\ +\ p_{\rm{B}}\)となります.
(2)のとき
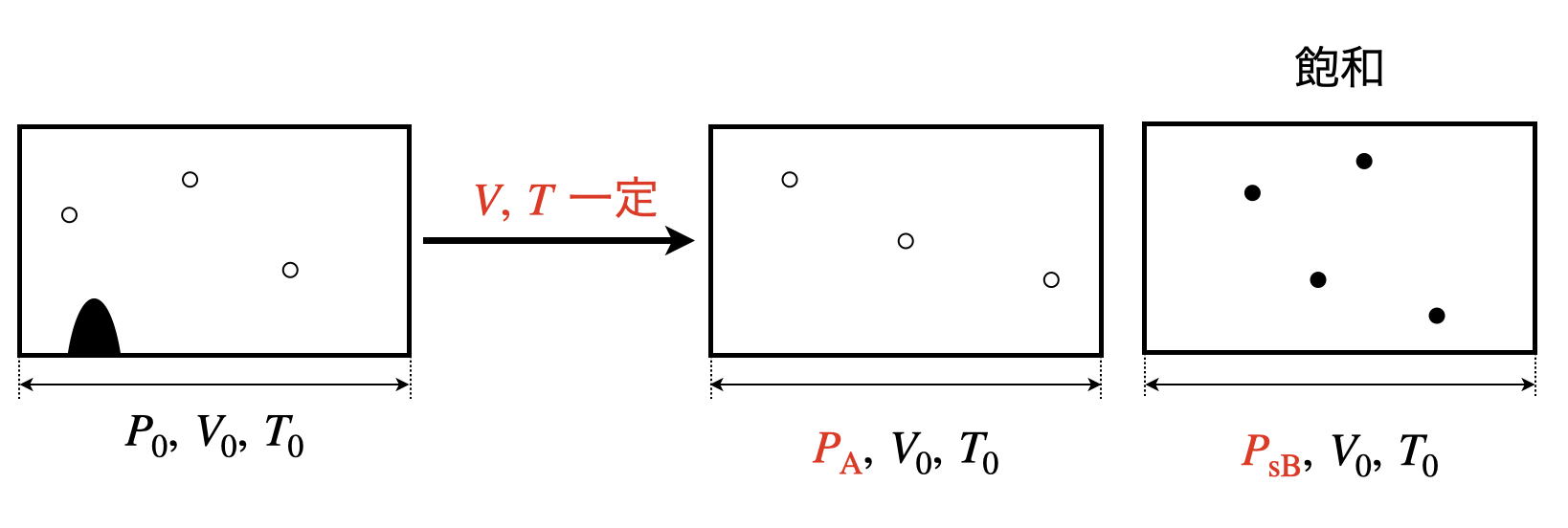
(\(2\))のとき,\(p_{\rm{B}}\ =\ p_{\rm{sB}}\)となっています.
状態図より,液体は境界線ギリギリで全て蒸発し,気体になっていることが分かります.
そのため物質\(B\)の圧力は\(p_{\rm{sB}}\)となります.
そのため,全圧は\(p_{\rm{A}}\ +\ p_{\rm{sB}}\)となります.
(3)のとき
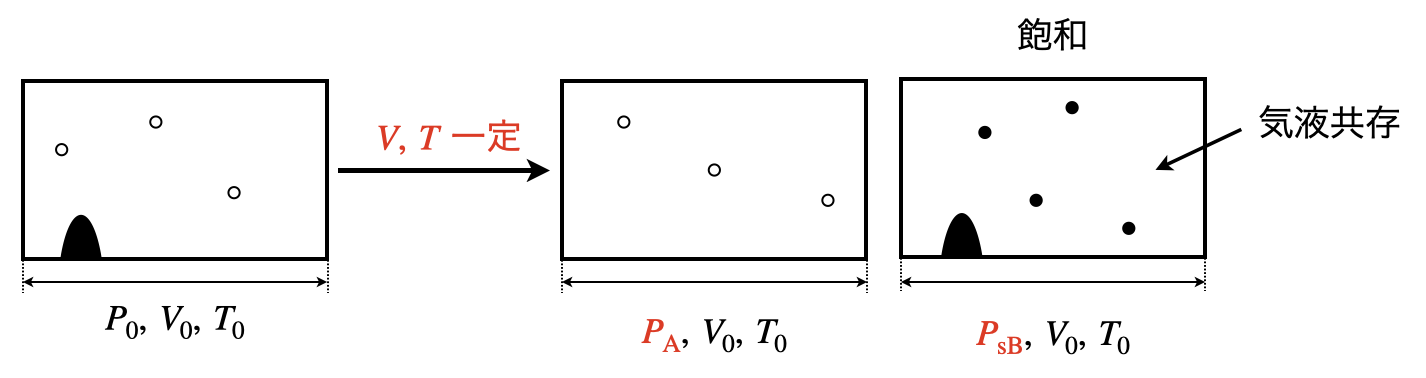
(\(3\))のとき,\(p_{\rm{B}}\ >\ p_{\rm{sB}}\)となっています.
このような状況では,物質\(A\)が存在し,容器内を飛び回っています.
物質\(B\)が蒸発して気体になる空間は存在しています.
そのため,先程の節の(\(1\))の状況に相当します.
物質\(B\)は気体の他に液体が存在しており,気液共存状態となっています.
このときの物質\(B\)の圧力は\(p_{\rm{sB}}\)となります.
そのため,全圧は\(p_{\rm{A}}\ +\ p_{\rm{sB}}\)となります.



コメント