
電子式
まずは電子式の基礎から復習していきましょう!
原子中の価電子は,\(2\)個で対になったときに安定します.このように逆向きのスピンをもつ\(2\)個の価電子が対になったものを電子対,対にならずにひとりで存在しているものを不対電子といいます.つまり,対になっていない(不対)電子ということですね.電子式では,電子対を「・・」,不対電子を「・」として表します.
具体的に第\(2\)周期の元素の電子配置を見てみましょう.
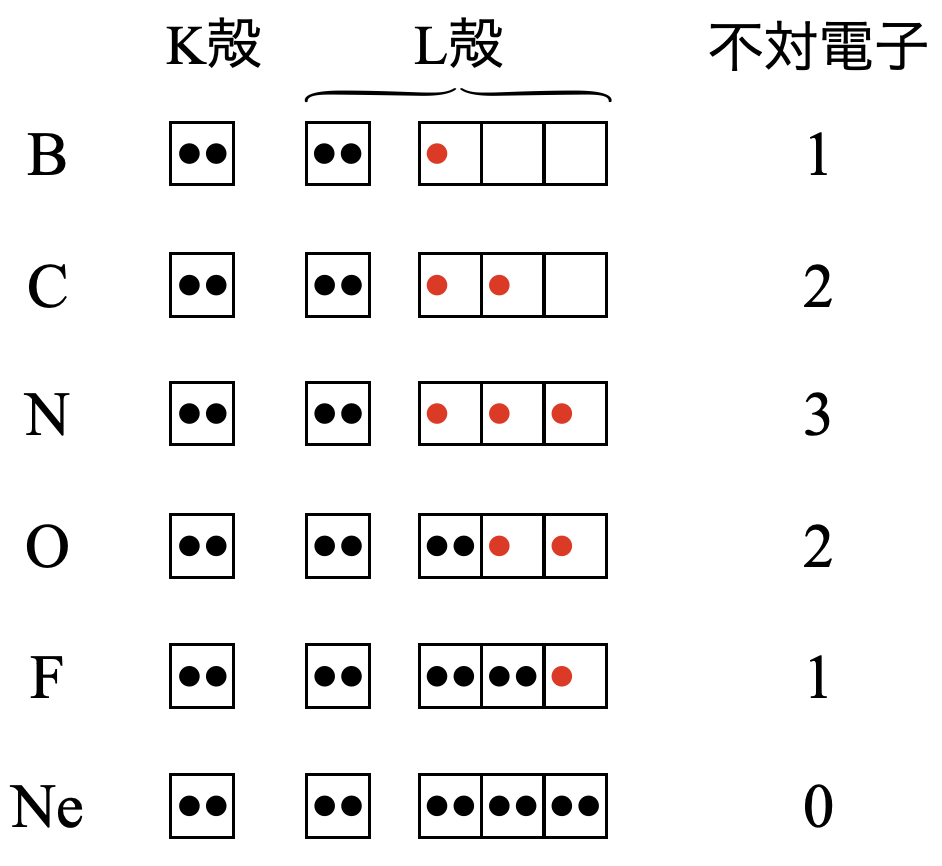
以上の原子の最も安定な電子配置を見ていくと,
「不対電子数が最大となる電子配置をとる」
ということです.これは非常に大切な点です.
そのため例えば\(\rm{O}\)原子について,下のようになることはない!ということです.
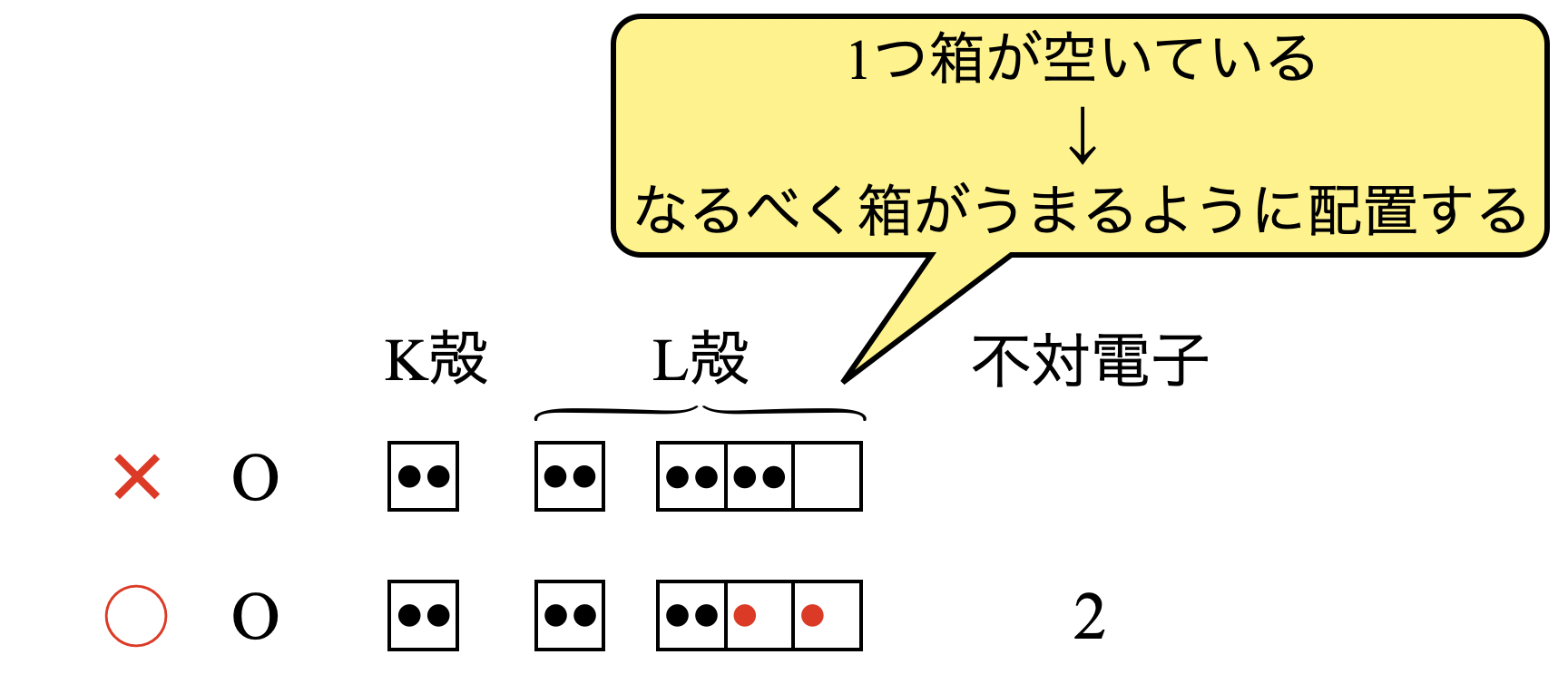
そしてこれらの電子配置をわかりやすく表示すると以下のようになります.このとき第\(2\)周期の元素については,\(\rm{L}\)殻の電子配置のみを示すというきまりがあります.

構造式
試験などでは見知らぬ物質と出くわすことがあります.そのときに構造式を聞かれたとします.
みなさんどうしますか?
覚えている物質しか構造式を書けないようではすべて暗記しなければいけません…そこで,この疑問にしっかりと答えられるような解法を今から丁寧に解説していきます!
以下の\(5\)ステップでどの物質についても完璧に構造式を書くことができるようになります.
\(\rm{Step1:}\)最外殻電子数の合計(\(x\))を求める
\(\rm{Step2:}\)周りの電子に\(8\)個電子を置き,その合計(\(y\))を求める
\(\rm{Step3:}\)足りない電子数(\(x\ – y\))を中心に配置する
\(\rm{Step4:}\)電子の調整をする
\(\rm{Step5:}\)電子の所有者をチェックする
言葉だけではまったくわからないと思いますので,二酸化炭素(\(\rm{CO_2}\))を例として説明していきます!
\(\rm{Step1}\)
まずは\(\rm{C}\)と\(\rm{O}\)のそれぞれの最外殻電子数(\(x\)とします)を求めます.最大殻電子数を数えると,\(\rm{C}\)原子が\(4\)コ,\(\rm{O}\)原子が\(6\)コであるため,
\(x = 4 + 6 × 2 = 16\)コ
となります.
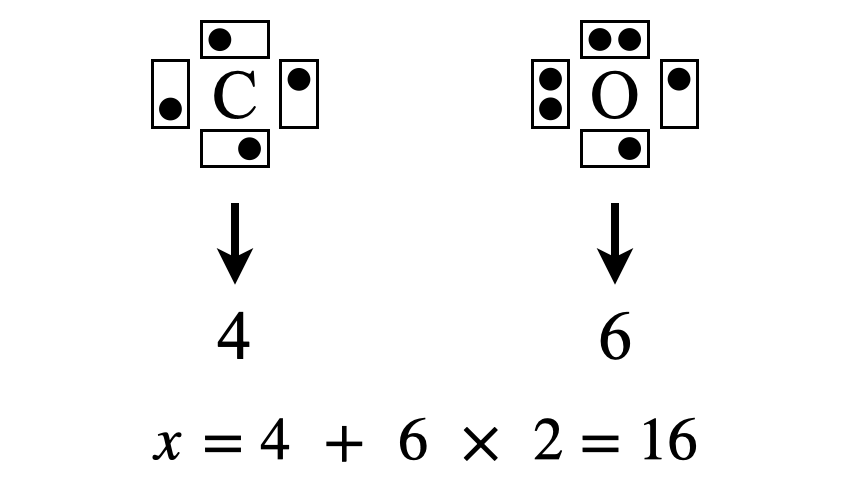
\(\rm{Step2}\)
中心に\(\rm{C}\)原子を,その周りに\(\rm{O}\)原子を置きます.そして\(\rm{C}\)原子の周りにある\(\rm{O}\)原子に\(8\)個の電子数を置き,その合計を求めます(\(y\)とします).
\(y = 8 × 2 = 16\)コ
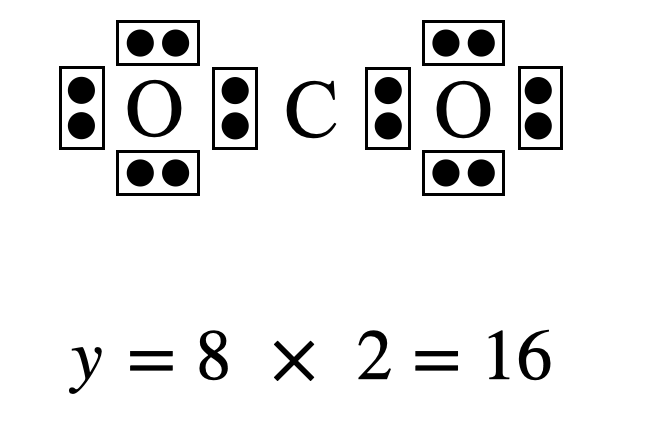
\(\rm{Step3}\)
ここで,\(x\ – y\)を求め,足りない電子数を中心原子の周りに配置します.今回の場合は,\(x\ – y = 16\ – 16 = 0\)となるので,この操作をする必要はありません.
\(\rm{Step4}\)
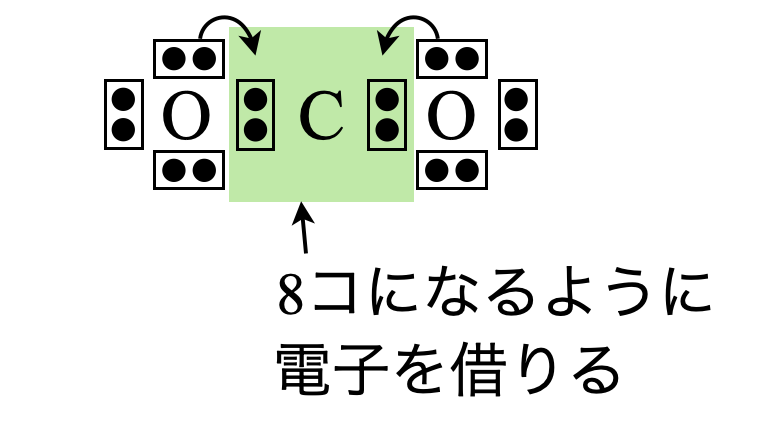
中心にある\(\rm{C}\)原子の周りの電子数が\(8\)個となるように隣にある\(\rm{O}\)原子から電子をもらいましょう!このように\(\rm{O}\)原子から電子を借りることで,\(\rm{C}\)原子の周りの電子数が\(8\)個となり,電子式が完成しました.
\(\rm{Step5}\)
最後にそれぞれの電子の所有者をチェックしておく必要があります.所有者が自分でないのにその電子を使っているのであれば,それは他の電子からの借り物であり,結合で考えると配位結合となります.
この場合も周りに存在する原子から考えていきましょう!
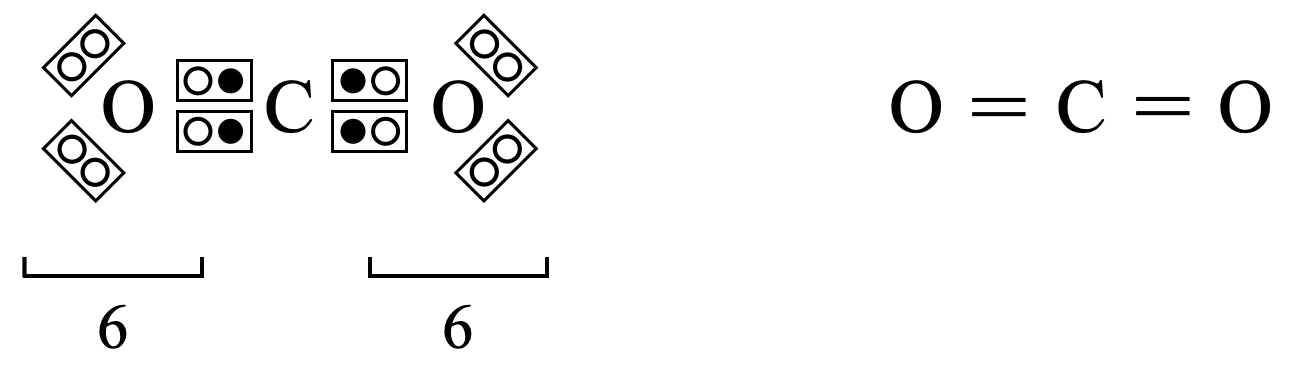
\(\rm{O}\)原子の最外殻電子数は\(6\)コなので,\(\rm{C}\)原子と\(\rm{O}\)原子間の結合はそれぞれが電子を出し合って結合,つまり共有結合であることがわかります.これより\(\rm{CO_2}\)の構造式は下のようになります.
一通り構造式の書き方を理解したところで,下の練習問題を解いてみましょう!テストによく出てくる物質から一度は練習しておいてほしい物質を厳選しました.この練習問題を解くことで,この\(5\)ステップを自分のものにしていきましょう!
練習問題
次の分子,イオンの電子式と構造式を書いてください.
\(\rm{(1)NH_3}\) \(\rm{(2)SO_2}\) \(\rm{(3)NO_3^-}\)
それでは\(1\)つずつ丁寧に考えていきましょう!
(\(1\))
まず,それぞれ\(x\)と\(y\)を求めていきましょう.
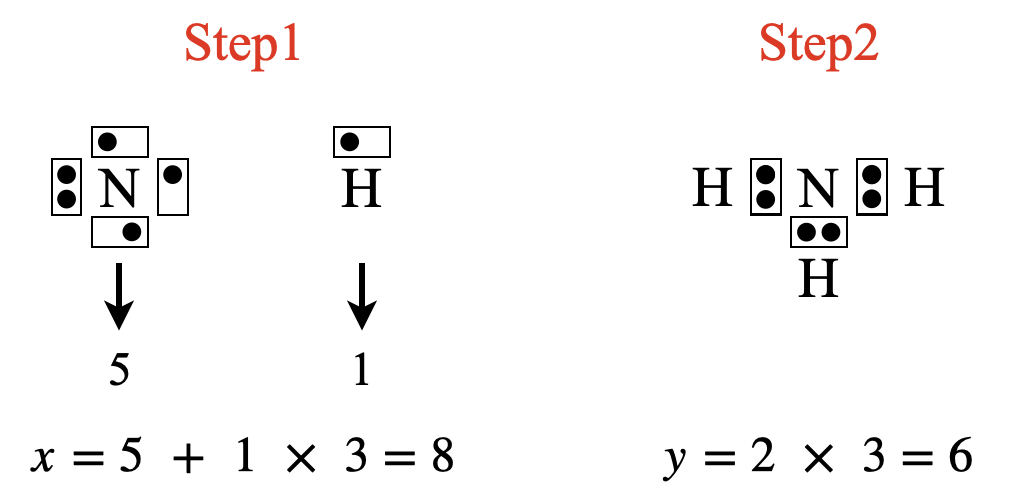
\(\rm{NH_3}\)の場合は,\(x = 5 + 1 × 3 = 8\)コ,\(y = 2 × 3 = 6\)コ
ここで,\(\rm{H}\)原子については例外があります.\(\rm{H}\)原子の周りに置く電子数は,\(2\)コにしてください!
\(x\ – y = 8\ – 6 = 2\)コなので,\(\rm{N}\)原子の周りに\(2\)コ電子を追加します.すると,\(\rm{N}\)原子の周りの電子数は\(8\)コとなり\(\rm{OK}\)です!

最後に電子の所有者をチェックしておきましょう!
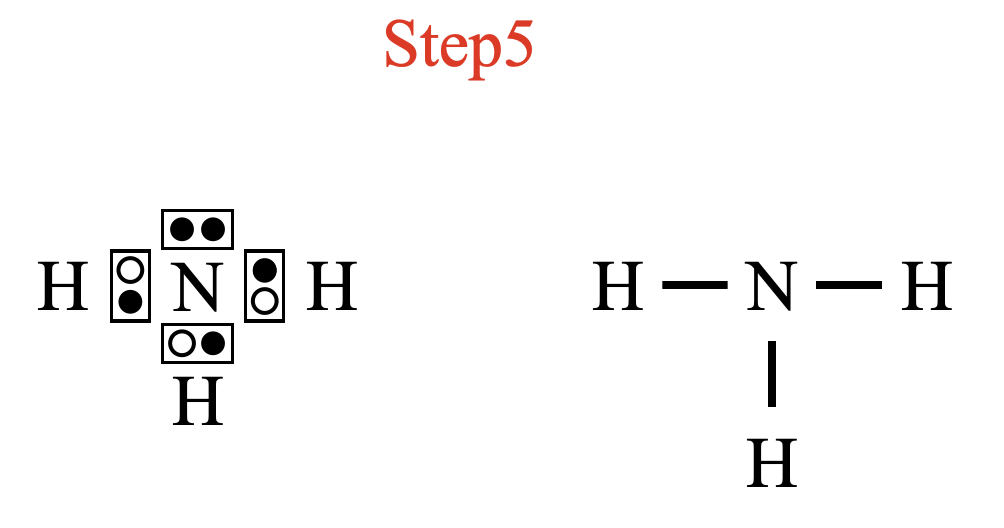
\(\rm{H}\)原子の最外殻電子は\(1\)コなので,それぞれ電子対を共有している共有結合であることがわかります.これから電子式と構造式は次のようになります.
(\(2\))
今回もやり方はまったく同じです.
\(\rm{SO_2}\)の場合は,\(x = 6 + 6 × 2 = 18\)コ,\(y = 8 × 2 = 16\)コ
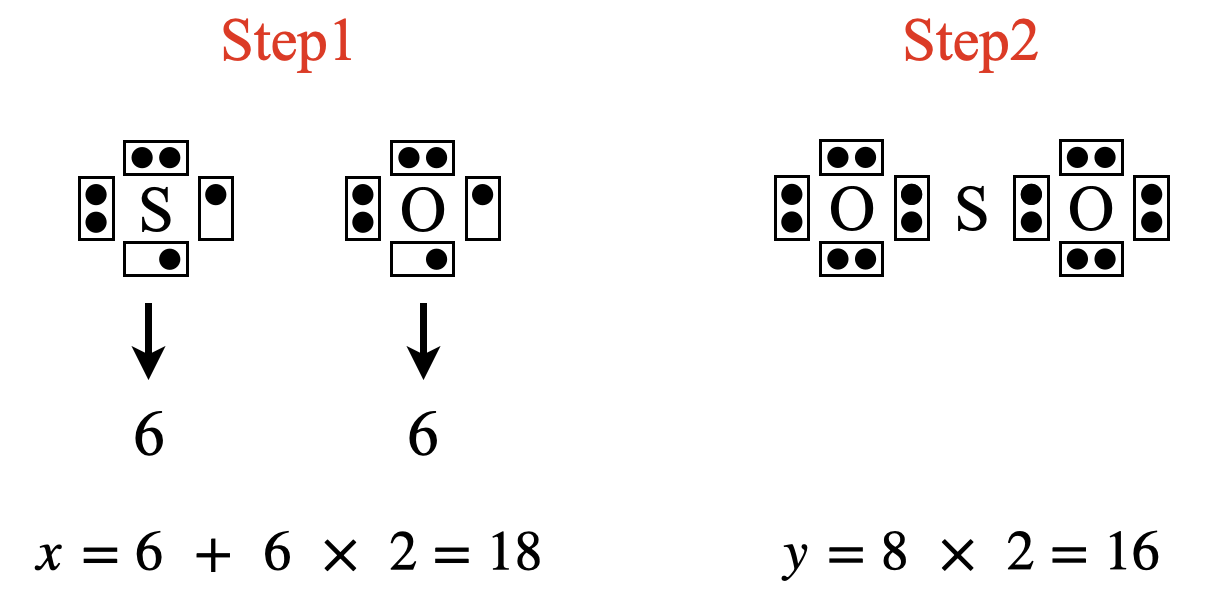
\(x\ – y = 18\ – 16 = 2\)コなので,\(\rm{S}\)原子の周りに\(2\)コ電子を追加します.
次に,\(\rm{S}\)原子の周りの電子数が\(8\)コとなるように\(\rm{O}\)原子から電子を\(2\)コ借りてきます.これによって\(\rm{S}\)原子の周りの電子数は\(8\)コとなりました!
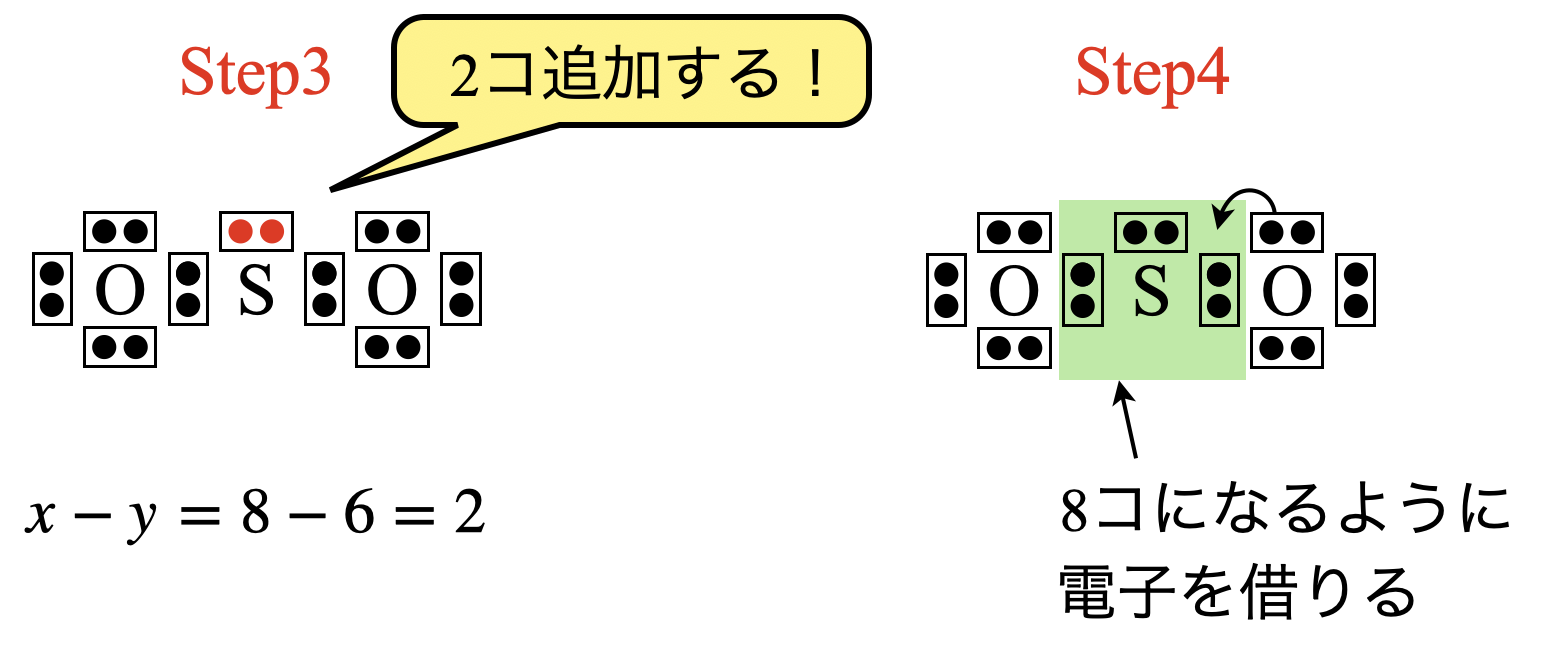
最後に電子の所有者のチェックを忘れずにしておきましょう!
\(\rm{O}\)原子の最外殻電子は\(6\)コなので,\(\rm{O:S}\)結合に関しては\(\rm{S}\)原子からの借り物であることがわかります.そのため,これは配位結合となり,\(\rm{O←S}\)と表すことができます.これから電子式と構造式は次のようになります.
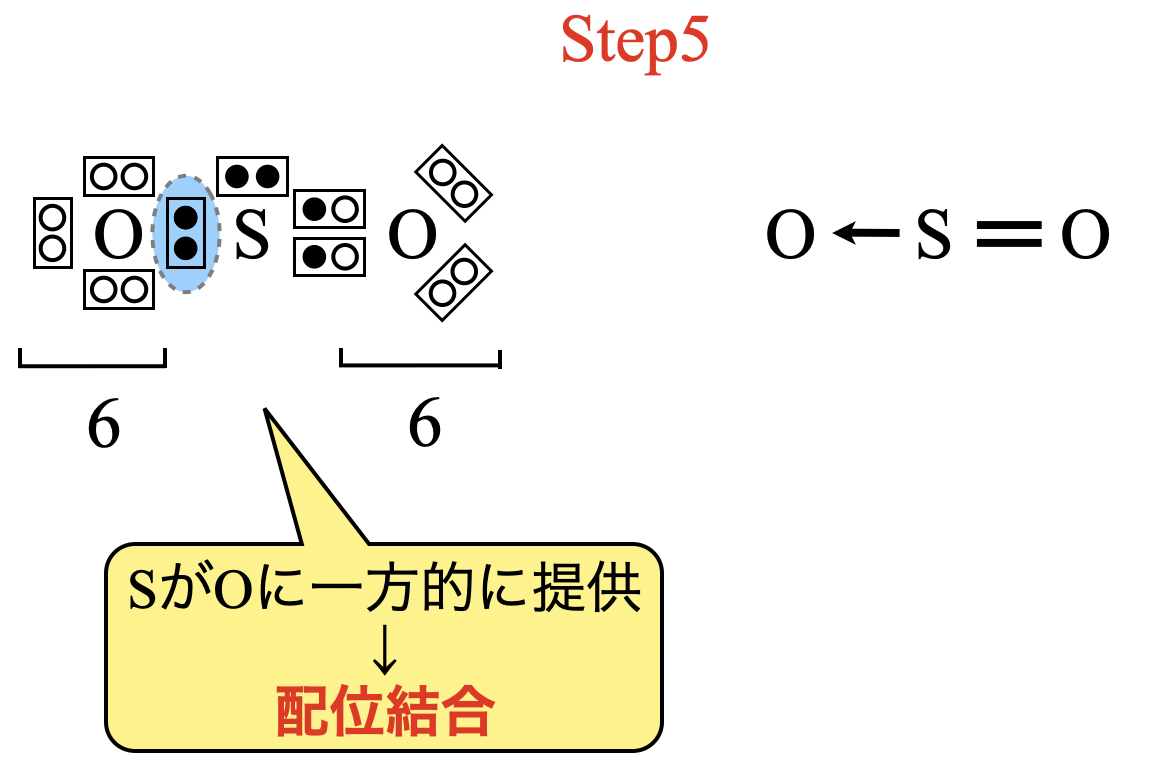
物質によって,配位結合をもつものともたないものがあります.
\(\rm{Step5}\)は必要ないのでは?と思う方もいるかもしれませんが,\(\rm{SO_2}\)のような物質のために毎回チェックを怠らないようにしましょう!
(\(3\))
今回もやり方はまったく同じです.
\(\rm{NO_3^-}\)の場合は,\(x = 5 + 6 × 3 + 1 = 24\)コ,\(y = 8 × 3 = 24\)コ
\(x\)をカウントするときに,陰イオンであるため,「\(+1\)」を忘れないでくださいね!
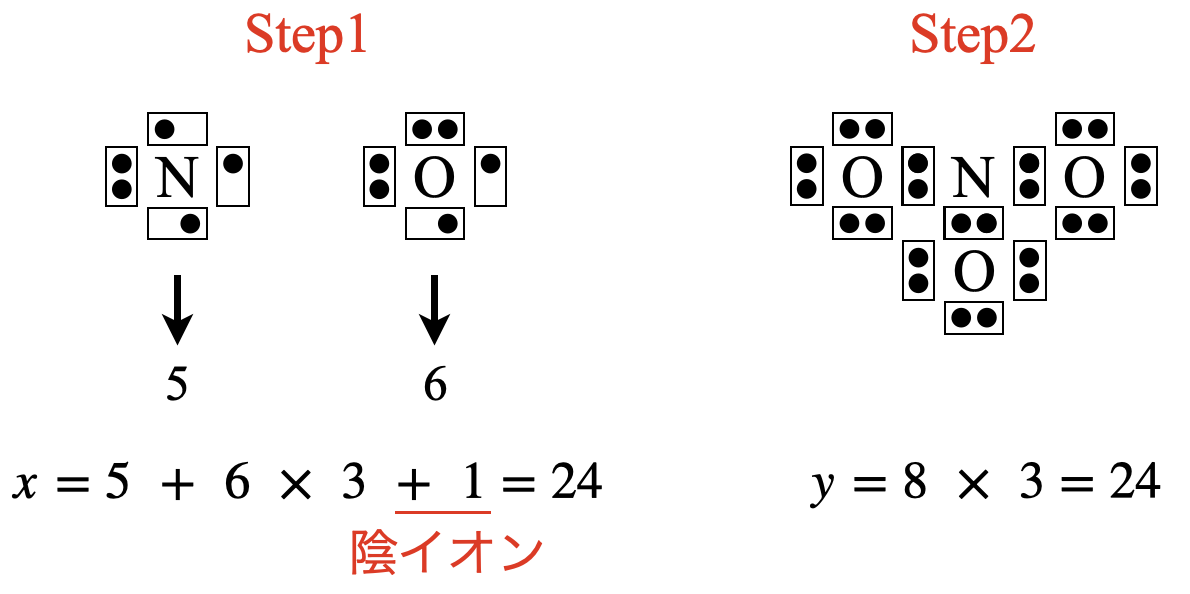
\(x\ – y = 24\ – 24 = 0\)コなので,電子を追加する必要はありません.
次に,\(\rm{N}\)原子の周りの電子数が\(8\)コとなるように\(\rm{O}\)原子から電子を\(2\)コ借りてきます.これによって\(\rm{N}\)原子の周りの電子数は\(8\)コとなりました!

最後に電子の所有者をチェックしておきましょう!
\(\rm{O}\)原子の最外殻電子は\(6\)コなので,\(\rm{O}\)と\(\rm{N}\)の結合の\(1\)つが配位結合であることがわかります.これから電子式と構造式は次のようになります.
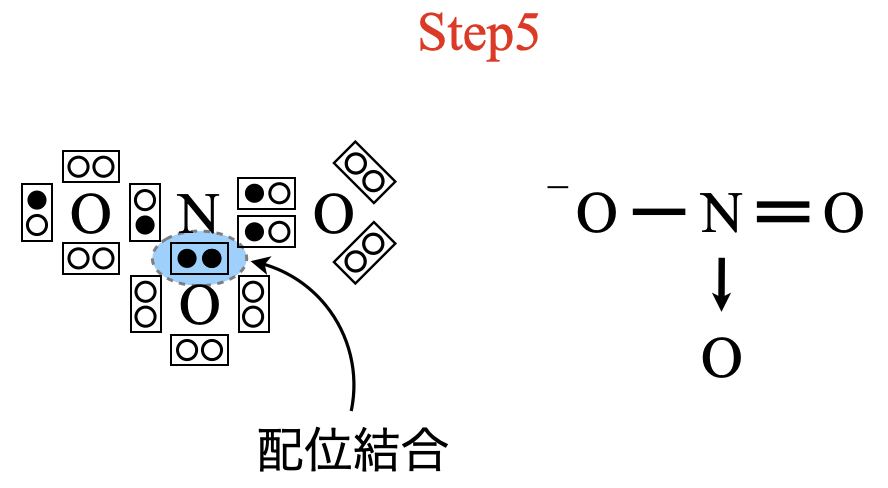
形の推定
ここまで読み進めていただいただけでもかなりレベルアップしています!これからさらに一歩踏み込んで,電子式から形の推定を行います.
形の推定については,電子の気持ちになれば理解することができます!笑 といってもそんな精神論だけではなく,しっかりとその論理的に説明していきますね!
\(\rm{H}\)原子をのぞいて全ての原子が\(4\)つの電子対をもっています.その\(4\)つの電子対の配置パターンを考えると次の\(3\)パターンが存在します.
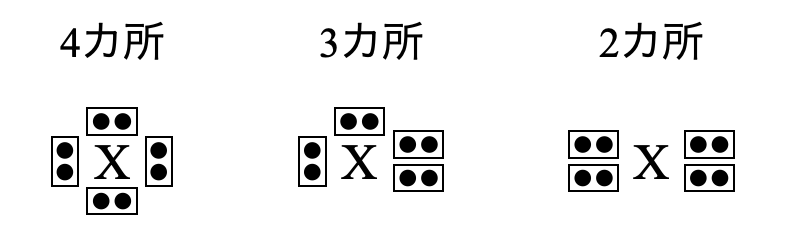
これらの電子対は負の電荷をもっているため,互いに電気的に反発し合います.そのためその反発をできるだけ避けるように配置していると考えられます.人間でも嫌いな人とは少し距離をおいたりしますよね?そんなイメージです笑
すると,電子配置が\(4\)カ所のときは正四面体の方向へ,\(3\)カ所のときは正三角形の方へ,\(2\)カ所のときは直線の左右方向へ配置されると考えられます.
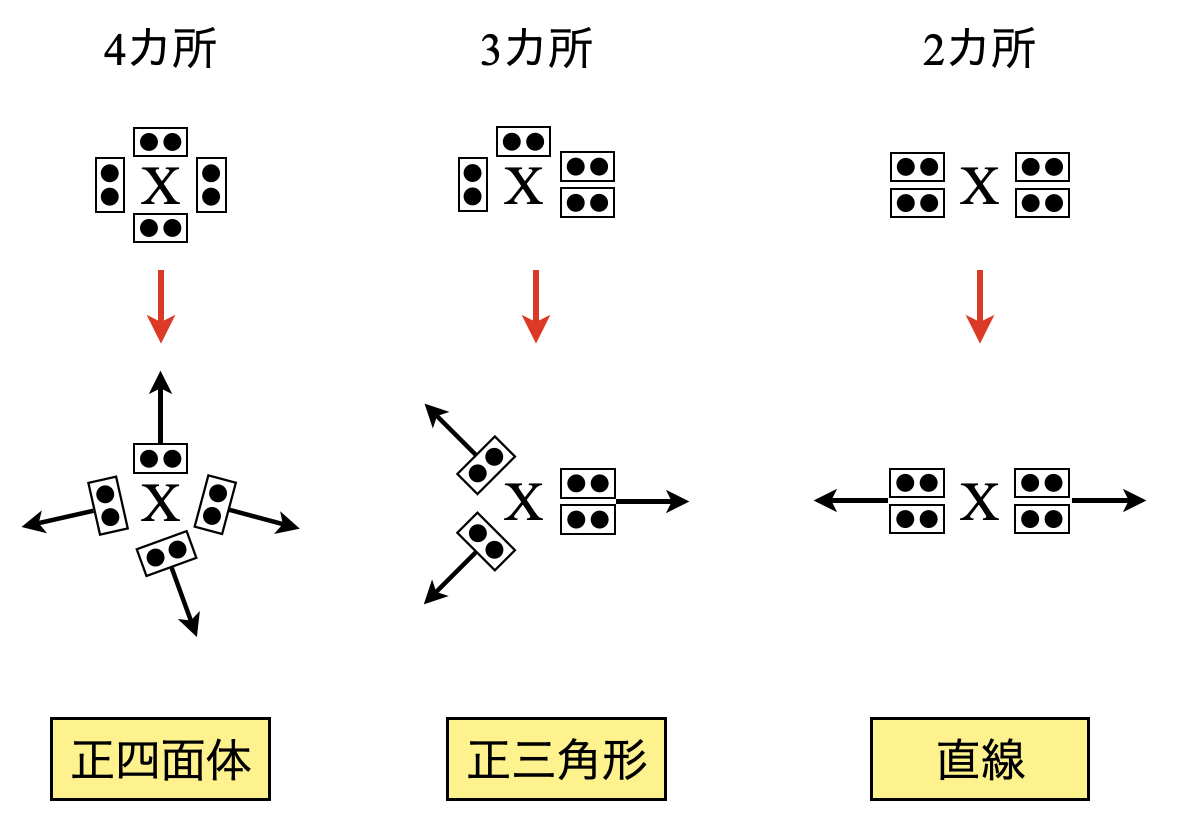
この考え方をもとに次では具体的に\(3\)ステップで解説していきます!
具体的な\(3\)ステップ
以下の\(3\)ステップを行うことで,どの物質についても形を推定することができます.
\(\rm{Step1:}\)電子式を決定する
\(\rm{Step2:}\)電子対が何カ所あるのか確認する
\(\rm{Step3:}\)電子対の配置を確認する
二酸化硫黄(\(\rm{SO_2}\))を例として考えていきましょう!
\(\rm{Step1}\)
先程の練習問題から\(\rm{SO_2}\)の電子式はわかります.
\(\rm{Step2}\)
\(\rm{SO_2}\)の電子式を見ると,中心の\(\rm{S}\)原子には電子対が\(3\)カ所あることがわかります.そのため三角形方向に電子が反発します.
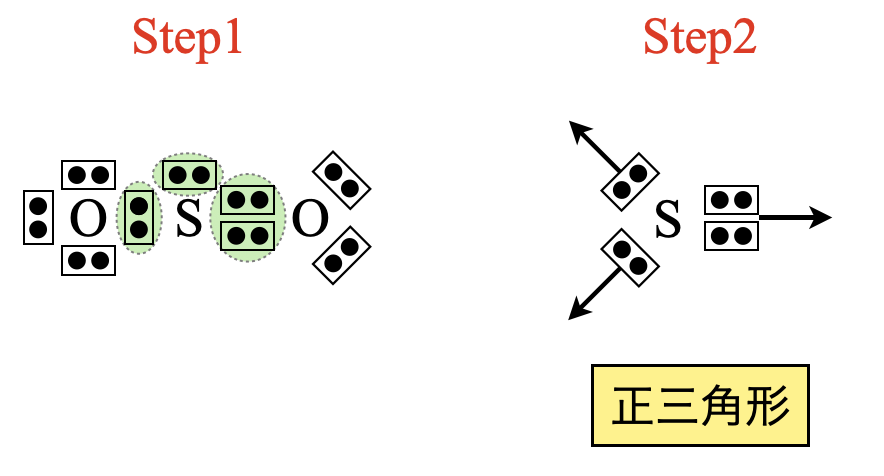
\(\rm{Step3}\)
結合状態について考えると,\(\rm{O←S=O}\)と\(\rm{O=S→O}\)が頻繁に入れ替わっている状態なので,\(\rm{O}\)と\(\rm{S}\)の左右の結合は同じような状態にあると考えて\(\rm{OK}\)です.そのため\(\rm{SO_2}\)は二等辺三角形と推定できます.
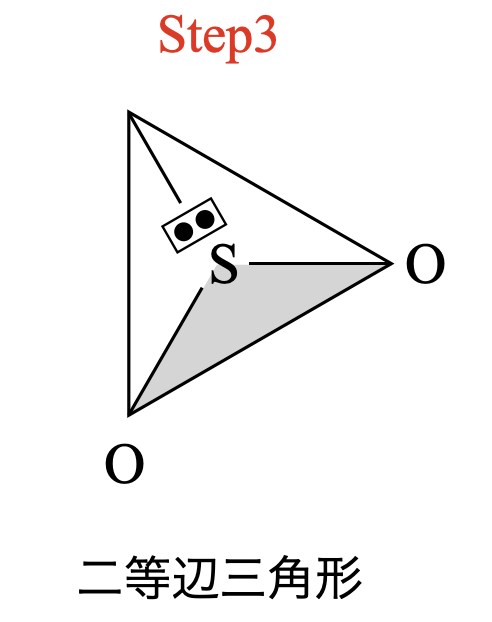
それでは練習問題を解いていきながら,様々なパターンを練習していきましょう!
練習問題
以下の分子,イオンの形を推定してください.
\(\rm{(1)CH_4}\) \(\rm{(2)NH_3}\) \(\rm{(3)H_2O}\) \(\rm{(4)SO_3}\)
丁寧に解いていきましょう!
(\(1\))
まずは電子式を書いていきましょう!これは先程の\(5\)ステップで書くことができます.
\(\rm{Step1}\)
\(\rm{CH_4}\)の場合は,\(x = 4 + 1 × 4 = 8\)コ,\(y = 2 × 4 = 8\)コ
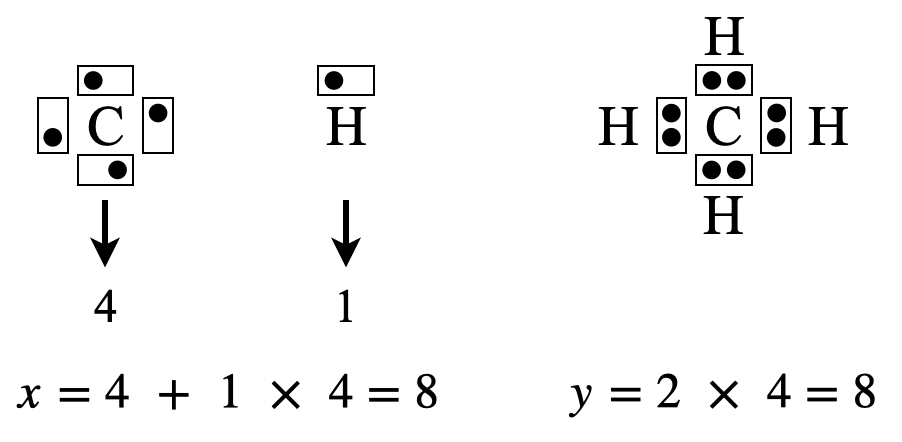
\(x\ – y = 8\ – 8 = 0\)コなので,電子を追加する必要はありません.
\(\rm{C}\)原子の周りの電子数は\(8\)コとなり,電子式はこのままで\(\rm{OK}\)です!
\(\rm{Step2}\)
\(\rm{CH_4}\)は電子対が\(4\)カ所あるので,正四面体の方向に配置します.
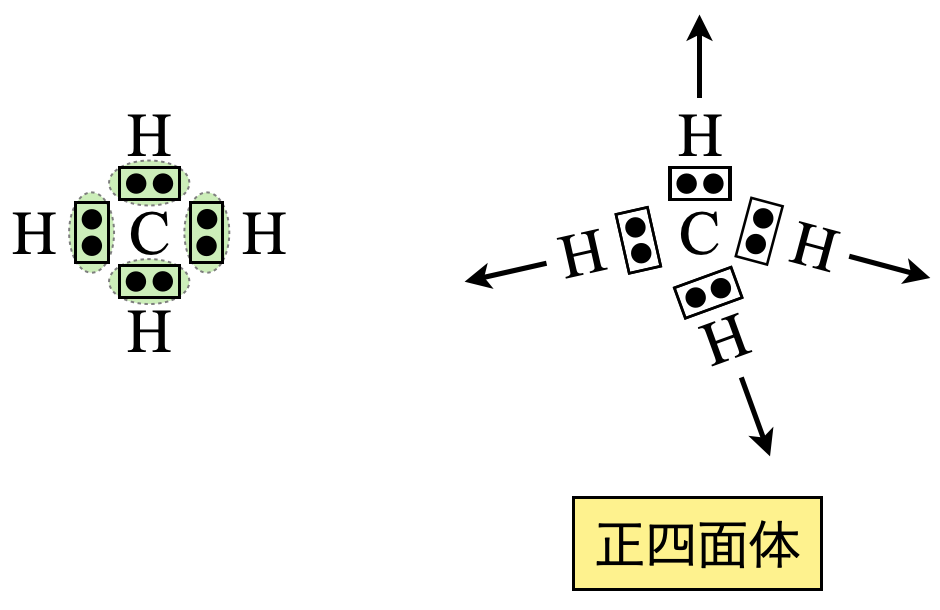
\(\rm{Step3}\)
これより\(\rm{CH_4}\)は正四面体になります.
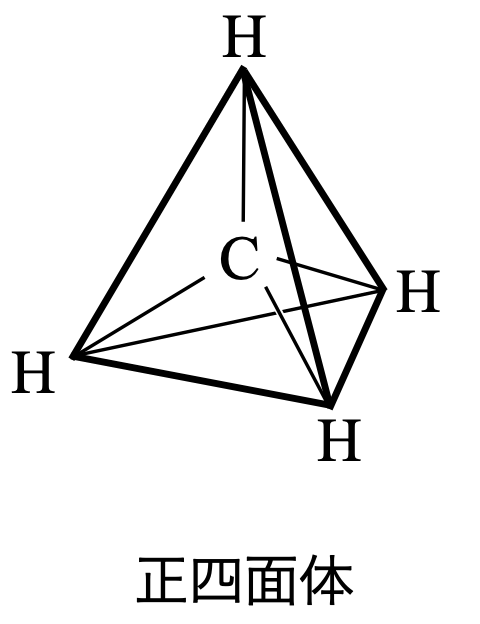
(\(2\))
次は\(\rm{NH_3}\)です.
\(\rm{Step1}\)
\(\rm{NH_3}\)は先程の練習問題\(1\)から電子式はわかっていますね!
\(\rm{Step2}\)
\(\rm{NH_3}\)についても電子対が\(4\)カ所あるので,正四面体の方向に配置します.
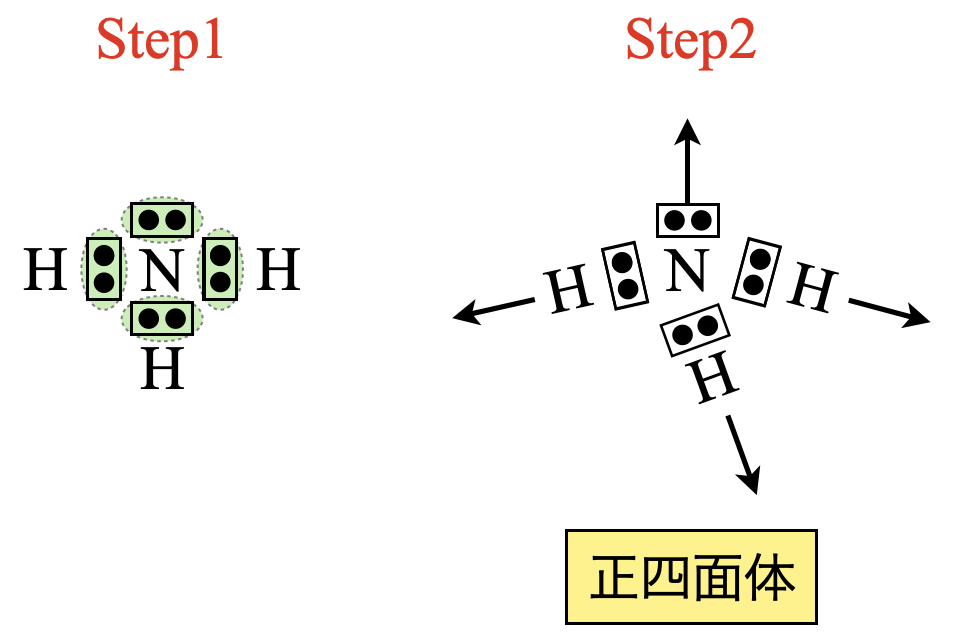
\(\rm{Step3}\)
正四面体の方向に配置しますが,非共有電子対が\(1\)つあるため,正三角錐となります.このように「形の推定では非共有電子対の存在を無視して形を推定」します!

(\(3\))
\(\rm{Step1}\)
まずは電子式を考えていきましょう.
\(\rm{H_2O}\)の場合は,\(x = 1 × 2 + 6 = 8\)コ,\(y = 2 × 2 = 4\)コ
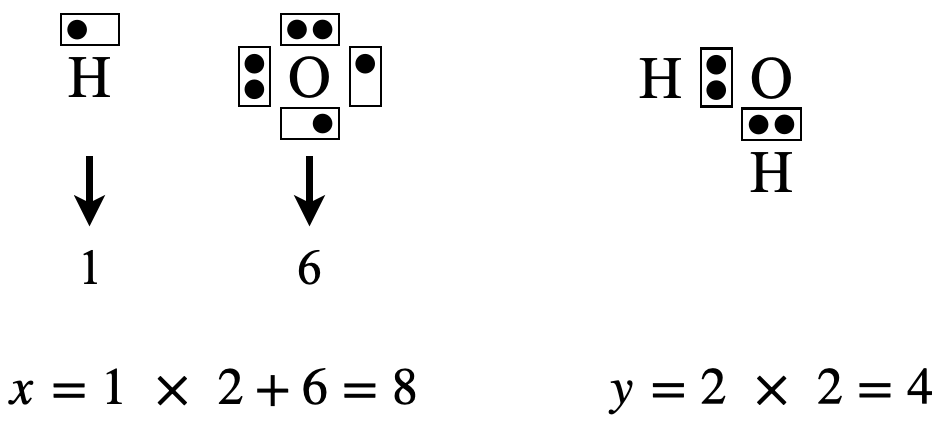
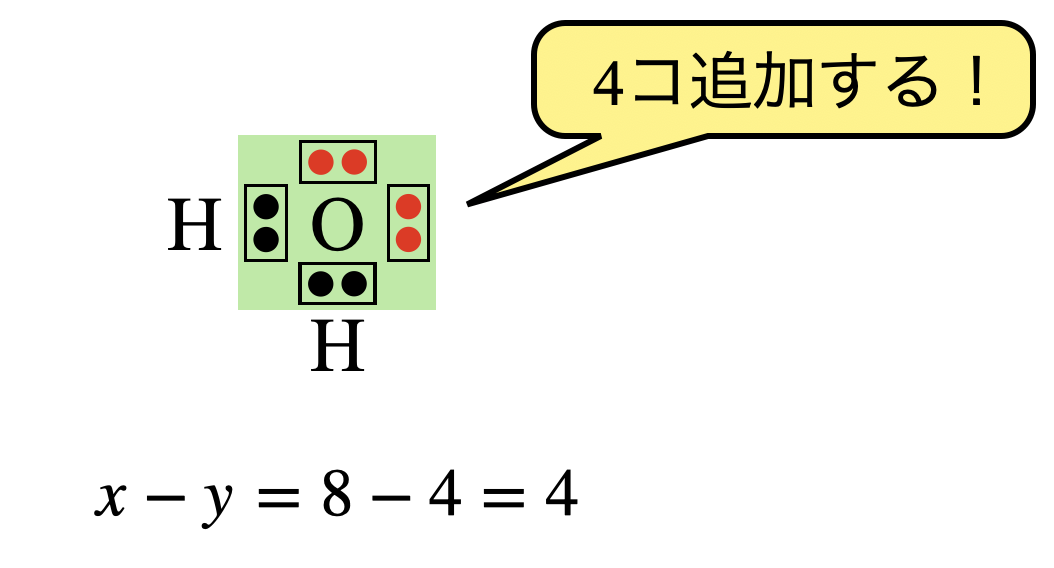
\(x\ – y = 8\ – 4 = 4\)コなので\(\rm{O}\)原子の周りに電子を\(4\)コ追加します.
すると,\(\rm{O}\)原子の周りの電子数は\(8\)コとなり,電子式は下のようになります.
\(\rm{Step2}\)
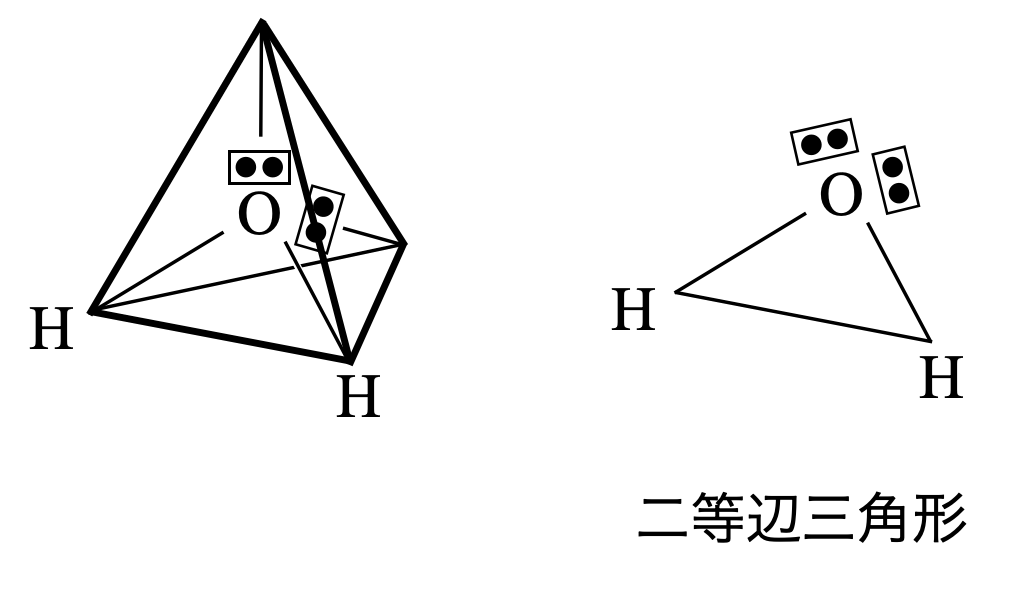
\(\rm{H_2O}\)についても電子対が\(4\)カ所あるので,正四面体の方向に配置します.
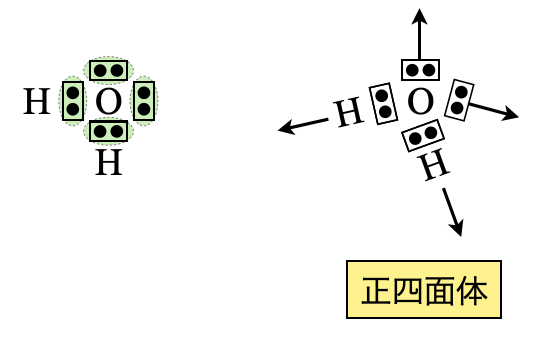
\(\rm{Step3}\)
正四面体の方向に配置しますが,非共有電子対が\(2\)つあるため,二等辺三角形となります.今回も非共有電子対があるため,その存在を無視して形を推定します.
(\(4\))
\(\rm{Step1}\)
まずは電子式を考えていきましょう.
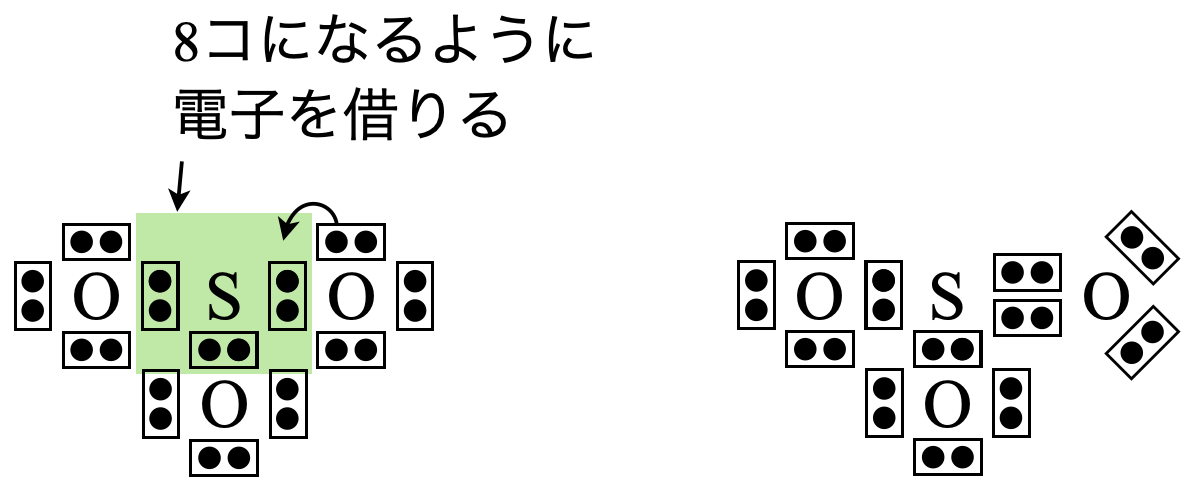
\(\rm{SO_3}\)の場合は,\(x = 6 + 6 × 3 = 24\)コ,\(y = 8 × 3 = 24\)コ

\(x\ – y = 24\ – 24 = 0\)コなので,電子を追加する必要はありません.
\(\rm{S}\)原子の周りの電子数が\(8\)コとなるように\(\rm{O}\)原子から電子を\(2\)コ借りてきます.これによって\(\rm{S}\)原子の周りの電子数は\(8\)コとなりました!
\(\rm{Step2}\)
\(\rm{SO_3}\)は電子対が\(3\)カ所なので,正三角形の方向に配置します.
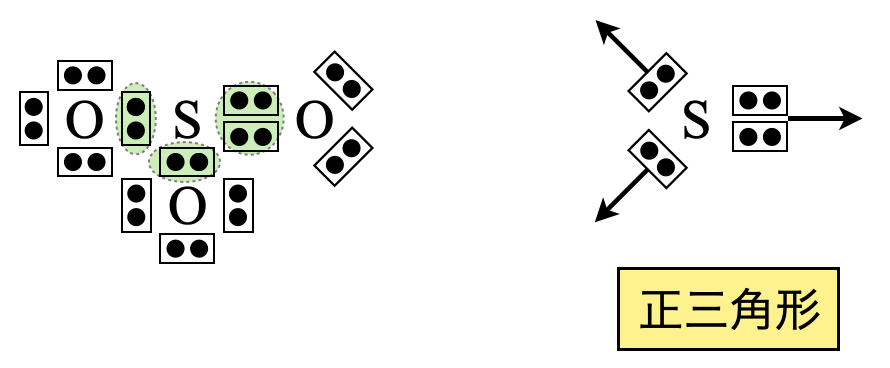
\(\rm{Step3}\)
これから正三角形と推定できます.

今日は以上です.お疲れ様です.
電子式の書き方から形の推定までを無理なくできるように解説してきました.
このステップをマスターすることで初めての物質と出会ってもしっかりと推定できると思います!わからない点があれば遠慮なくコメントくださいね!



コメント