
それでは今日も頑張っていきましょう!
解説してほしい分野があればぜひ次の記事のコメント欄で教えてくださいね!

\(\rm{You Tube}\)ではより具体的な問題を解説しているので,ぜひそちらもご覧ください!

凝固点降下
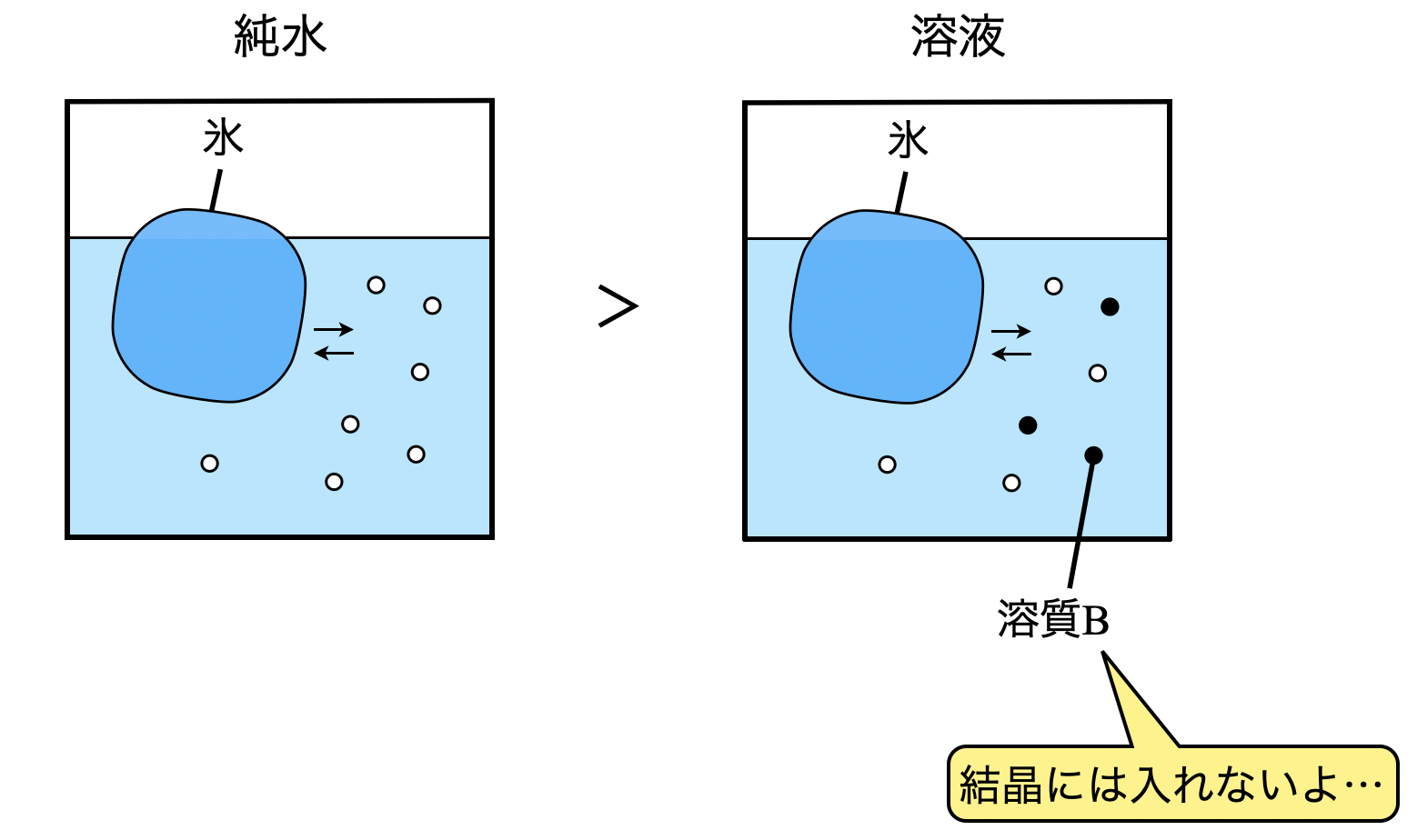
溶媒である水分子\(\rm{H_2O}\)と溶質\(\rm{B}\)を考えてみましょう.ここで,溶質\(\rm{B}\)については液の表面から蒸発しないとします.(この蒸発しないという性質のことを不揮発性といいます!)
この溶液を冷却して温度を下げていくと,氷が析出します.この氷は\(\rm{H_2O}\)分子が規則的に配列した結晶であり,この中には溶質\(\rm{B}\)は存在しません.つまり,凝固のときも「溶媒と溶質で別々の行動をとっています!」
\(\rm{H_2O}\)分子が固体になるとき,溶質分子がその邪魔をするため,固体に向かう粒子の量が減少します.そこで,より温度を低くして,固体になりやすくする必要があります.この現象を凝固点降下といいます.
凝固点降下は以下の式で表されます.
\(\Delta t = k_{\rm{f}} m\)
\(k_{\rm{f}}\):モル凝固点降下,\(m\):溶液の質量モル濃度です.つまり,蒸気圧降下や沸点上昇と同様に,質量モル濃度\(m\)に比例するということです.
状態図
それでは次に,状態図を使って理解していきましょう.
凝固点降下は\(\rm{101.3\ kPa}\)での固液平衡点に関する性質です.
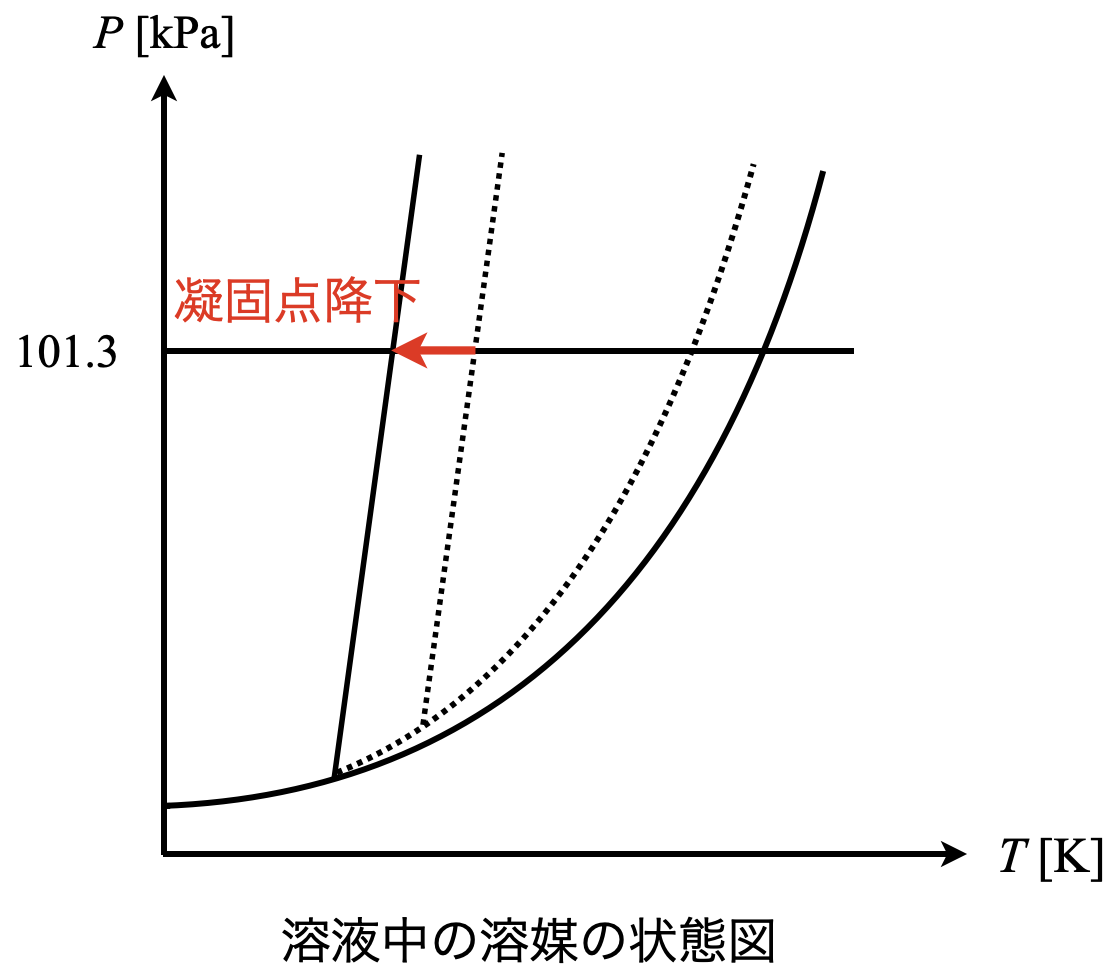
今まで学んできた状態図のまとめを示しておきます!覚えるときは,下の図で覚えてくださいね!

この図を見ると,溶質の添加によって状態図の液相が広がったことがわかります.蒸気圧降下・沸点上昇・凝固点降下は,これをどのポイントで見ているかの違いだけであることがわかります.
求め方も質量モル濃度\(m\)に比例します.この公式から見てもこれらは兄弟のような関係であることがわかりますね!
冷却曲線
冷却曲線は,純溶液と溶質が溶解した溶液によって異なるため,それぞれ分けて解説していきます.ただし,純溶液の冷却曲線が基本となるので,まずは純溶液の場合をしっかりと理解していきます!
純溶液
溶媒である水分子のみの純溶液を考えてみましょう.
この溶液の温度を下げると,固体が析出します.これをグラフにすると下のようになります.
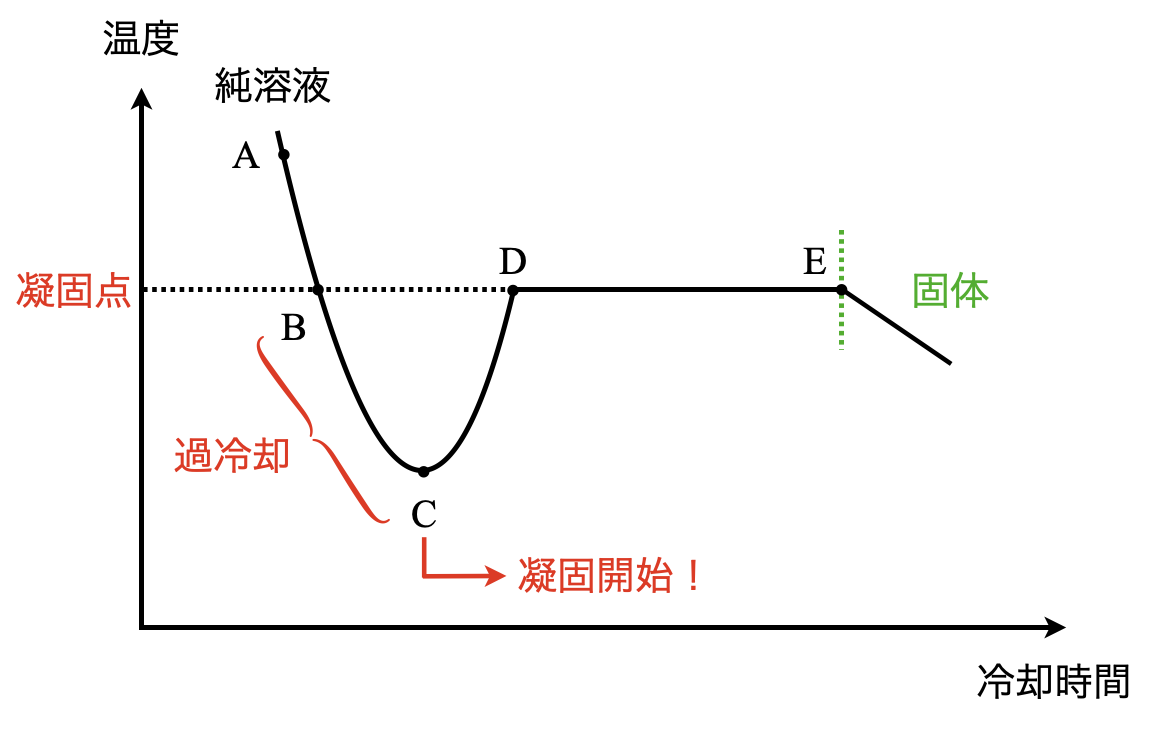
このグラフの見方を\(3\)ステップで解説していきます!
\(\rm{Step2}\):\(\rm{C}\)点で結晶が析出する
\(\rm{Step3}\):温度が\(\rm{D}\)点まで上昇して一定となる
\(\rm{Step1}\)
液の温度は時間とともに降下しますが,水の凝固点である\(\rm{0^\circ C}\)(\(\rm{B}\)点)になっても凝固は始まりません.凝固点以下の温度になっても,液体のまま存在している状態を過冷却といいます.
結晶が析出するためには,温度の条件に加えてある程度の大きさをもつ結晶核が存在する必要があります.過冷却が起こるのは,この結晶核がまだ存在していないためです.
結晶核は温度が低いほど生成しやすいため,過冷却が進むと,あるとき核が生成し,過冷却を脱します!
\(\rm{Step2}\)
\(\rm{C}\)点で過冷却状態を完全に解消し,外から奪った熱分だけ結晶が析出します.この点から凝固が開始します!
\(\rm{Step3}\)
冷却しているにもかかわらず温度が一定に保たれるのは,吸収した熱量の分だけ凝固が進み,発熱量\(=\)吸熱量というようにつりあっているからです.溶媒がすべて凝固すると,さらに温度が一定の割合で降下していきます.
溶液
純溶媒の冷却曲線をもとに,溶媒である水分子に溶質\(\rm{B}\)が溶解している溶液の冷却曲線を考えましょう.
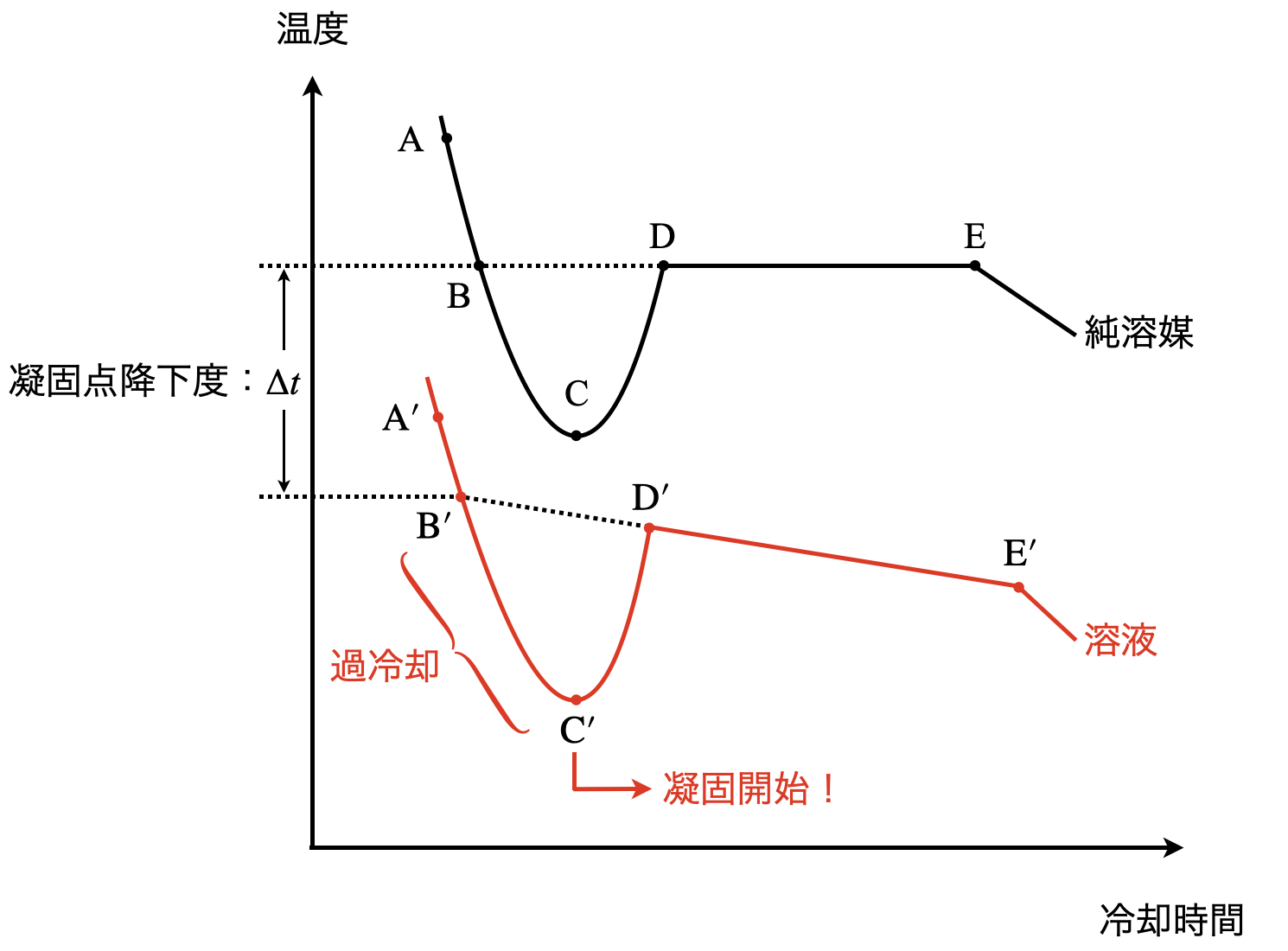
この冷却曲線の見方は\(2\)ステップでいきます!
\(\rm{Step2}\):凝固点(\(\rm{B’}\))の取り方に注意する
\(\rm{Step1}\)
溶液が凝固するとき,溶媒(\(\rm{H_2O}\))のみが凝固し,溶質\(\rm{B}\)については何も変化は起こりません.そのため,溶液の濃度は次第に増加していきます.
凝固点降下は公式から質量モル濃度に比例するので,濃度が高まるにつれて温度が低下していくというわけです!
\(\rm{Step2}\)
凝固点には注意が必要です.\(\rm{D’E’}\)を延長し,凝固前の冷却曲線と交差する\(\rm{B’}\)点が凝固点となります.そして\(\rm{B}\)点と\(\rm{B’}\)点の温度差\(\Delta t\)が凝固点降下度になります.
浸透圧
最後に浸透圧について解説していきましょう!
浸透圧は蒸気圧降下・沸点上昇・凝固点降下とは少し違う性質なので,兄弟ではなく,親戚といった雰囲気になります.
溶媒分子は通れるが,溶質\(\rm{B}\)は通れない半透膜という膜で仕切ることを考えます.
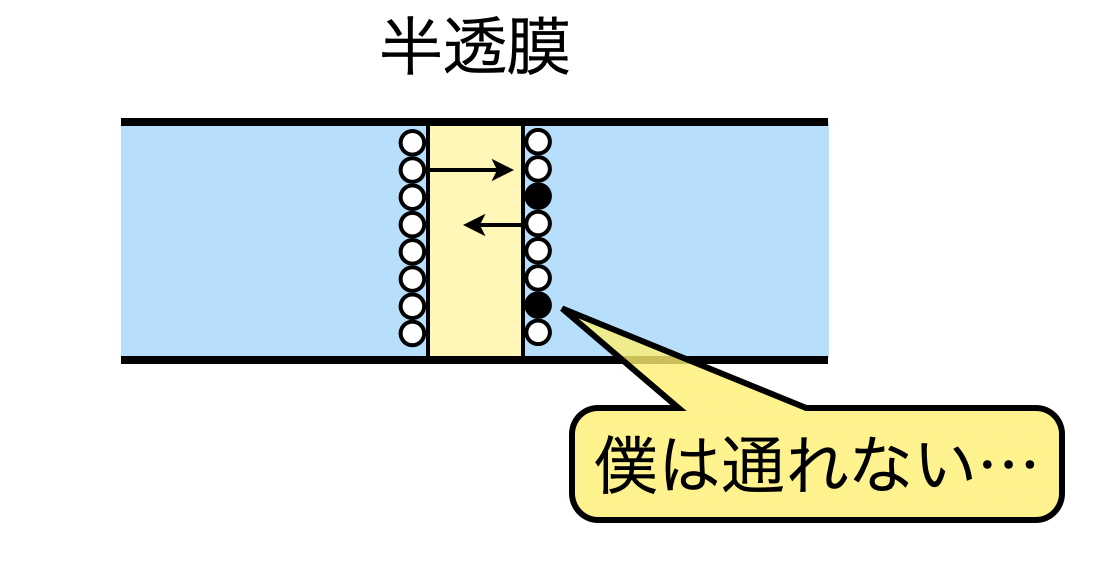
溶媒は通過でき,溶質は通過できないため,ここでも溶媒分子と溶質分子で別々の行動をとっていますね!
溶媒である水分子は半透膜を通過できるため,純水⇄溶液と自由に移動できます.ただ,溶液→純水への移動は,溶質\(\rm{B}\)が邪魔するため,移動できる水分子の数が少なくなります.この移動により,左右の液面差が生じに,あるところで平衡になることで水の浸透が止まります.
ここで,左右の液面差をなくすために溶液側に加える余分な圧力を浸透圧といいます.
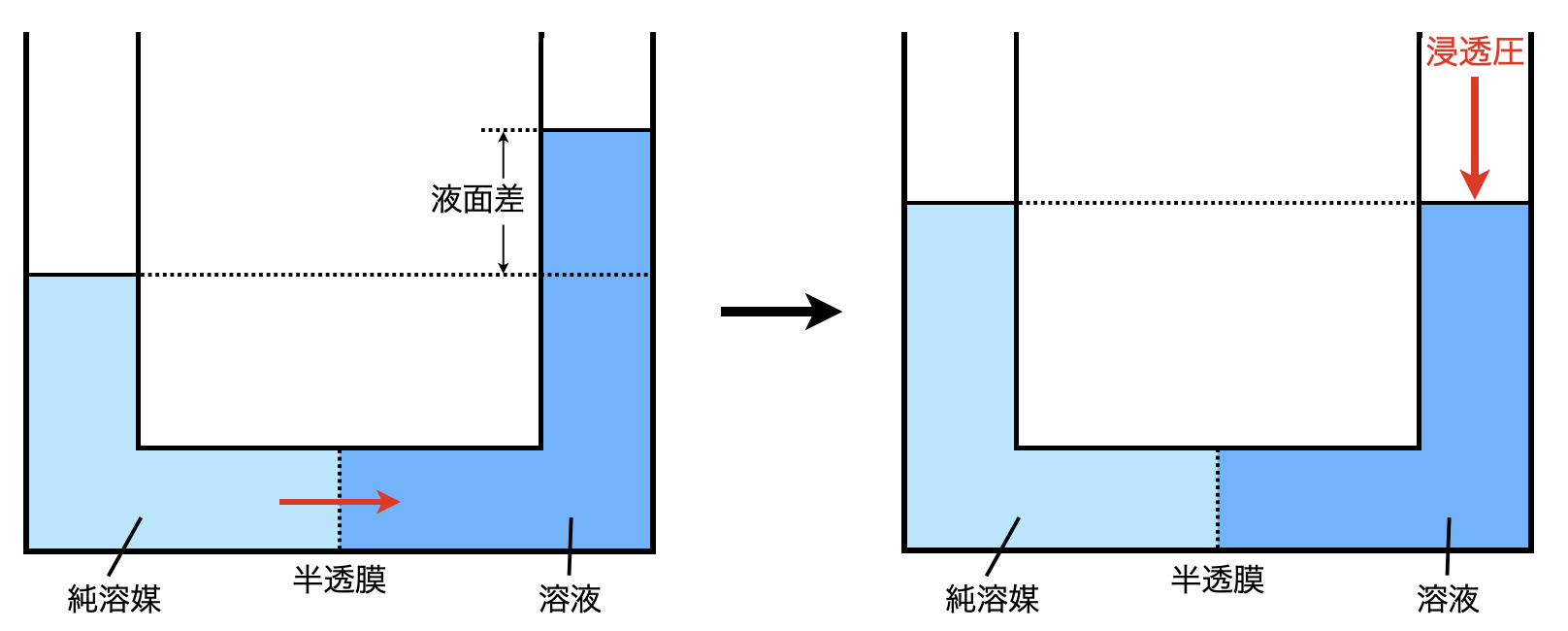
一般に浸透圧\(\Pi\)を求める公式は次のようになります.
\(\Pi = CRT\)
\(R\)は気体定数と一致しています.これをファントホッフの法則といいます.
また,\(C=\large \frac{n}{V}\)であるため,
\(\Pi V = nRT\)
となります!
なんとこれは,気体の方程式:\(pV = nRT\)と同じような形になっていることがわかります.これは覚えやすいですね!
練習問題
では,実際に問題を解きながら,理解を定着させていきましょう!まずは凝固点降下に関する問題です!
ベンゼンを冷却したところ,曲線\(\rm{A}\)の冷却曲線が得られた.次に,\(\rm{50.0\ g}\)のベンゼンに\(\rm{1.22\ g}\)のナフタレン\(\rm{C_{10}H_8}\)を溶解させ冷却すると,曲線\(\rm{B}\)の冷却曲線が得られた.
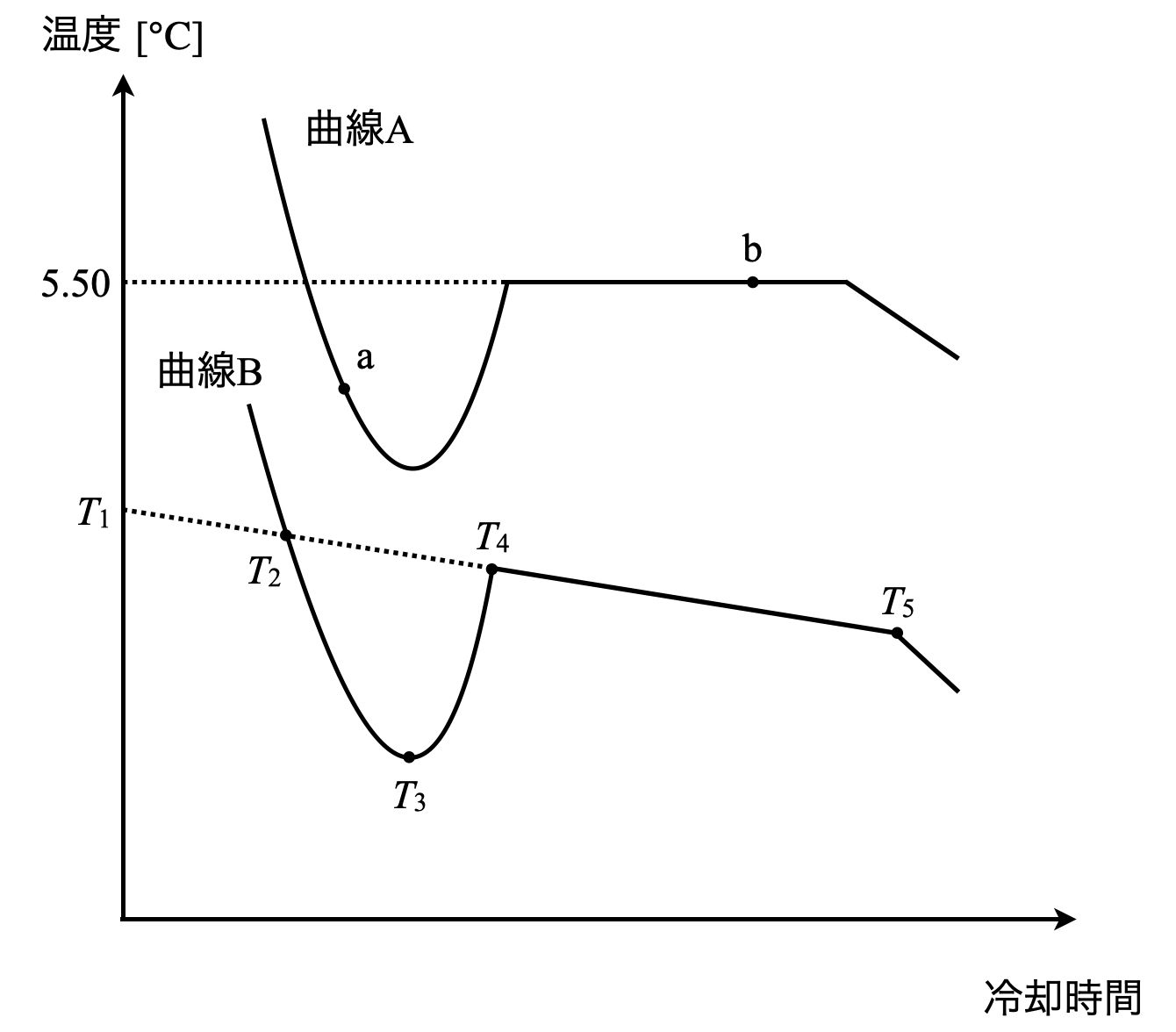
(\(1\))曲線\(\rm{A}\)の点\(\rm{a \cdot b}\)におけるベンゼンの状態は?
(\(2\))安息香酸のベンゼン溶液の凝固点は\(T_1\)〜\(T_5\)のいずれか?
(\(3\))ベンゼン\(\rm{50.0\ g}\)に\(\rm{0.500\ g}\)のナフタレン\(\rm{C_{10}H_8}\)を溶かして凝固点を測定したところ,凝固点は\(\rm{5.10^\circ C}\)であった.ベンゼンのモル凝固点降下 \(\rm{[K \cdot kg/mol]}\)は?
(\(1\))
\(\rm{a}\)
液体を冷却していくと,凝固点を過ぎても凝固せずに液体のままで温度が低下していきます.この現象を過冷却というのでしたね!
そのため,液体です.
\(\rm{b}\)
過冷却を脱して凝固が始まると,凝固熱が発生して液温は上がります.吸収した熱量の分だけ凝固が進み,発熱量=吸熱量というようにつりあっているのが\(\rm{b}\)の状態になります.
よって,液体と固体になります.
(\(2\))
\(T_4\)と\(T_5\)を結ぶ直線を左へ延長し,元の冷却曲線との交点\(T_2\)が凝固点になります.
(\(3\))
ベンゼンのモル凝固点降下とは,\(\Delta t = k_{\rm{f}}m\)の\(k_{\rm{f}}\)になります.これは\(2\)ステップで求めていきましょう!
\(\rm{Step2}\):質量モル濃度\(m\)を求める
\(\rm{Step1}\)
ナフタレン\(\rm{C_{10}H_8}\)を溶解させたときの凝固点が\(\rm{5.10^\circ C}\)です.そのため,温度差は
\(\Delta t = 5.50\ -\ 5.10 = \rm{0.40^\circ C}\)
\(\rm{Step2}\)
ベンゼン\(\rm{50.0\ g}\)に\(\rm{0.500\ g}\)のナフタレン\(\rm{C_{10}H_8}\)を溶かしています.ナフタレンのモル質量は\(\rm{128\ g/mol}\)なので,質量モル濃度は,
\(m = \large \frac{\frac{0.500}{128}\ \rm{[mol]}}{\frac{50.0}{1000}\ \rm{[kg]}} \small = \large \frac{5}{64}\ \small \rm{mol/kg}\)
これらの値を\(\Delta t = k_{\rm{f}} m\)に代入して\(k_{\rm{f}}\)を求めます.
\(0.40 = k_{\rm{f}} \cdot \large \frac{5}{64}\)
\(k_{\rm{f}} = 5.12\ \rm{K \cdot kg/mol}\)
今回はもう\(1\)問解説していきます!次は,浸透圧に関する問題です!
断面\(\rm{5.0\ cm^2}\)の\(\rm{U}\)字管の中央が半透膜で仕切られた容器の左側に純水\(\rm{50\ mL}\),右側にある非電解質\(\rm{X}\)がある一定量溶解している水溶液\(\rm{50\ mL}\)を入れて,\(\rm{300\ K}\)で放置した.その結果液面差が生じたため,\(\rm{U}\)字管の右側に\(\rm{77\ g}\)のおもりをのせ,両液面の高さをつりあわせた.水溶液の密度は\(\rm{1.0\ g/cm^3}\)とする.
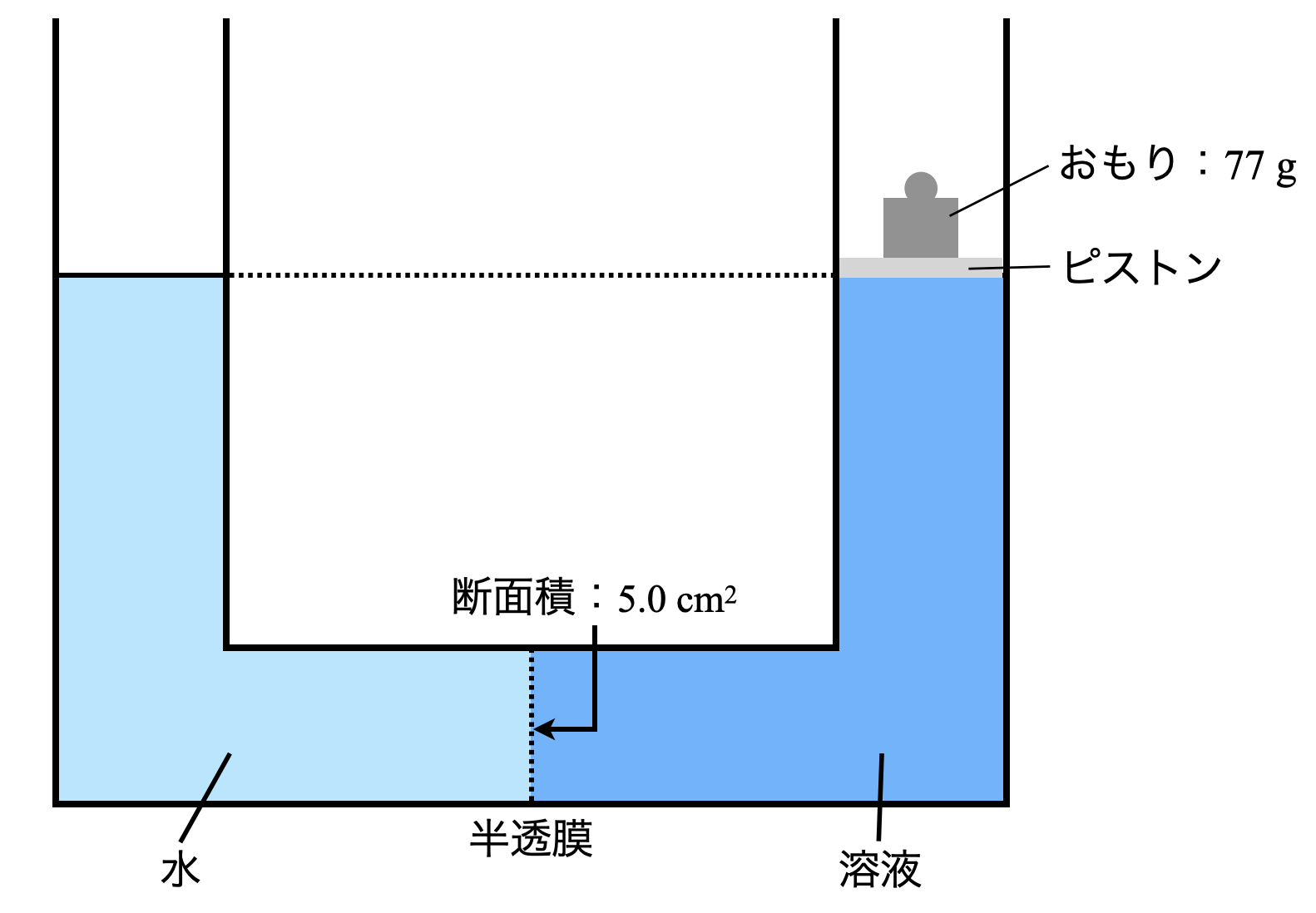
(\(1\))この溶液の浸透圧は何\(\rm{Pa}\)であるか?ただし,\(\rm{1.0 × 10^5\ Pa = 760\ mmHg}\)とし,水銀の密度を\(\rm{13.5\ g/cm^3}\)とする.
(\(2\))この水溶液\(\rm{50\ mL}\)中に含まれる非電解質\(\rm{X}\)は,何\(\rm{mol}\)であるか?
(\(3\))次におもりを取り除いて放置すると,水溶液の液面が次第に上昇した.このときの左右の液面差は何\(\rm{cm}\)であるか?
この問題はなかなか難易度の高い問題ですが,大事なポイントがたくさん詰まっていますので,しっかりと理解していきましょう!
(\(1\))
まず,この問題を見て「なんで水銀が出てくるの?」と思われた方が多いのではないでしょうか?」その感覚を持たれている方が正しいですよ!私も受験生の頃は同じように疑問でした!
ただし,これは単位換算のために水銀が登場しただけ!ということがわかり,スッキリしたのを覚えています!
これから以下の\(2\)ステップで詳しく解説していきますね!
\(\rm{Step2}\):単位換算をする
\(\rm{Step1}\)
まず,おもりによって左右の液面の高さが等しいので,おもりによる圧力と溶液の浸透圧がつりあっているということになります.
では,おもりによる圧力を求めましょう!ここで,圧力の単位の意味をしっかりと覚えておく必要があります.
圧力とは,「単位面積(\(\rm{1\ cm^2\ or\ 1\ m^2}\)など)あたりに働く力」という意味です.
これを今回出てくる単位で考えると,\(\rm{g/cm^2}\)となります.よって,おもりによる圧力は,断面積が\(\rm{5.0\ cm^2}\)なので,
\(\large \frac{77\ \rm{g}}{5.0\ \rm{cm^2}} \small = 15.4\ \rm{g/cm^2}\)
となります.
\(\rm{Step2}\)
求める圧力の単位を見ると,\(\rm{Pa}\)となっていますが,\(\rm{Step1}\)で求めたのは\(\rm{g/cm^2}\)でした.そのため,\(\rm{g/cm^2→Pa}\)に変換する必要があります.ここで,「水銀」という魔法の物質を使って変換していきます!
最初にまとめておくと,下のような流れになります.
①液柱の圧力(\(\rm{g/cm^2}\))→水銀柱の高さ(\(\rm{cmHg}\))
水銀の密度が\(\rm{13.5\ g/cm^3}\)と与えられているので,これらの値を使って水銀柱に換算したときの水銀柱の高さを求めることができます.
\(\rm{Hg}\)の高さ:\(\large \frac{15.4\ \rm{g/cm^2}}{13.5\ \rm{g/cm^3}} \small = 1.1407\ \rm{cmHg}\)
②水銀柱の高さ(\(\rm{cmHg}\))→パスカル(\(\rm{Pa}\))
ここでさらに問題文から\(\rm{Hg}\)の高さ\(\rm{760\ mm=76\ cm}\)が\(\rm{100\ kPa}\)であることが記載されています.そのため,\(\rm{1.1407\ cmHg}\)のときの圧力(\(\rm{Pa}\))がわかるというわけです.
\(1.1407 × \large \frac{100}{76} \small = 1.5\ \rm{kPa} = 1.5 × 10^3\ \rm{Pa}\)
なぜこの問題で水銀を使ったのかというと,これはたまたまではありません.
\(1643\)年にトリチェリーというイタリアのおじさんが水銀を用いて研究をしていました.そして標準的な大気圧\(\rm{101.3 \ kPa=760\ mmHg}\)であるということを発見しました.これは水銀柱\(\rm{760\ mm=76\ cm}\)が\(\rm{101.3 \ kPa}\)と等しいということです.
これによって先ほど説明したように,溶液の高さからパスカル(\(\rm{Pa}\))を求めることができるのです!他の問題でも出てくることがあるので,しっかりと計算方法をおさえておきましょう!
(\(2\))
求める物質量を\(n\ \rm{[mol]}\)とします.先ほど解説した浸透圧の公式:\(\Pi V = nRT\)を使って求めていきましょう!
\(1.5 × \large \frac{50}{1000} \small = n × 8.3 × 300\)
\(n ≒ 3.0 × 10^{-5}\ \rm{mol}\)
(\(3\))
液面差が\(x\ \rm{[cm]}\)のときに両液面がつりあったとします.

液面差が\(x\ \rm{[cm]}\)あるとき,純水→溶液側に移動した水は,\(\large \frac{x}{2}\ \small \rm{[cm]}\)分だけ浸透したことになります.底面積が\(\rm{5.0\ cm^2}\)なので,
\(5.0 × \large \frac{x}{2} \small = 2.5x\ \rm{[mL]}\)
このときの浸透圧と溶液の体積を求めましょう!
①浸透圧
先ほどと同じように求めていきます!
\(\rm{Step1}\)
\(5 × x = 5x\ \rm{[cm^3]}\)
密度を\(\rm{1\ g/cm^3}\)と考えてよいので,\(5x\ \rm{[g]}\).さらに断面積は\(\rm{5.0\ cm^2}\)なので,
\(\large \frac{5x\ \rm{[g]}}{5.0\ \rm{cm^2}} \small = x\ \rm{[g/cm^2]}\)
\(\rm{Step2}\)
\(\rm{Hg}\)の高さ:\(\large \frac{x\ \rm{g/cm^2}}{13.5\ \rm{g/cm^3}} \small = \large \frac{x}{13.5}\ \small \rm{[cmHg]}\)
\(\rm{Step3}\)
最後に,\(\rm{cmHg→Pa}\)に変換していきます.
\(\large \frac{x}{13.5} \small × \large \frac{100}{76}\ \small \rm{[Pa]}\)
先ほどと同じように\(3\)ステップで求めることができますね!
②溶液の体積
もともと\(\rm{50\ mL}\)あり,さらに\(2.5x\ \rm{[mL]}\)加わったため,
\(\large \frac{50\ +\ 2.5x}{1000}\ \small \rm{[L]}\)
となります.
これらの値を浸透圧の公式:\(\Pi V = nRT\)を用いて\(x\)を求めていきます!
\(\large \frac{x}{13.5} \small × \large \frac{100}{76}\ \small × \large \frac{50\ +\ 2.5x}{1000} \small = 3.0 × 10^{-5} ×8.3× 10^3 × 300\)
\(x^2\ +\ 20x\ -\ 308 = 0\)
\(x≒10\ \rm{cm}\)
となります.最後の計算は結構めんどくさいですが,頑張ってください…笑
今日は以上となります.本当にお疲れ様でした.
練習問題が2題と多くて難しかったと思いますが,本当に大切な内容を厳選しているので,しっかりと復習して解けるようにしてくださいね!疑問があれば遠慮なくコメントくださいね!



コメント