
- \(\rm{COD}\)のイメージをもつ(なぜその操作を行うのか?)
- 酸化剤・還元剤の\(e^-\)に注目する
- 攻略\(4\)ステップを完全理解する
を特にポイントとしています.昨日の自分より少しでもレベルアップしていきましょう!
解説してほしい分野があればぜひ次の記事のコメント欄で教えてくださいね!

\(\rm{COD}\)とは?
\(\rm{COD}\)とは,\(\rm{Chemical}\)(化学的) \(\rm{Oxygen}\)(酸素) \(\rm{Demand}\)(要求量)のことです.これを聞いただけでは,なんのことはわからないと思いますので,かみくだいて解説していきます.
\(\rm{COD}\)を理解するためには,酸化還元の基礎的な知識が必要となります.酸化剤や還元剤などの知識に不安がある方は以下の中から不安なものについて読んでみてください!

\(\rm{COD}\)とは,水中に有機物がどれだけあるのかを酸素の質量に換算して数値化したものです.
ここで,なぜ有機物に注目するのでしょうか?
水中に有機物があると,その有機物と結合した窒素やリンをプランクトンが利用することで,有害プランクトンが大量増殖してしまいます.これが赤潮の原因となります.
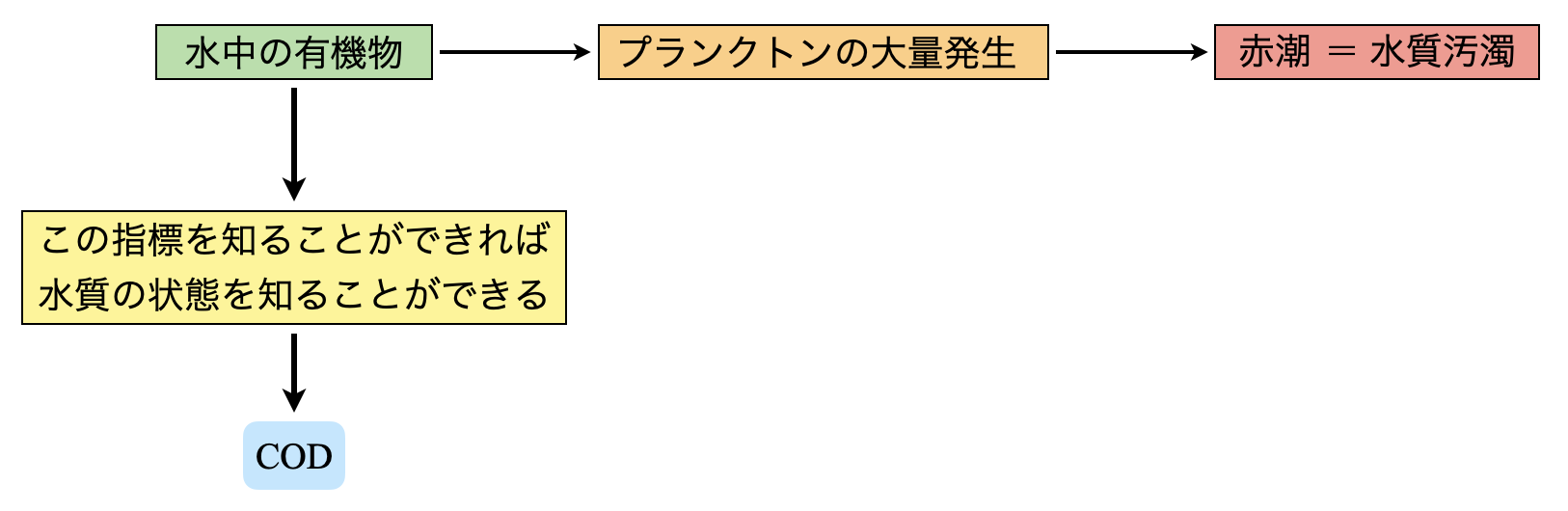
この流れを考えると,水中の有機物量を測定することが,その川や海の汚染量を測定することにつながることがわかると思います.\(\rm{COD}\)では,水中(\(\rm{1\ L}\))に存在する有機物を酸化させ,その酸化に必要な酸素質量(\(\rm{mg}\))で示しています.
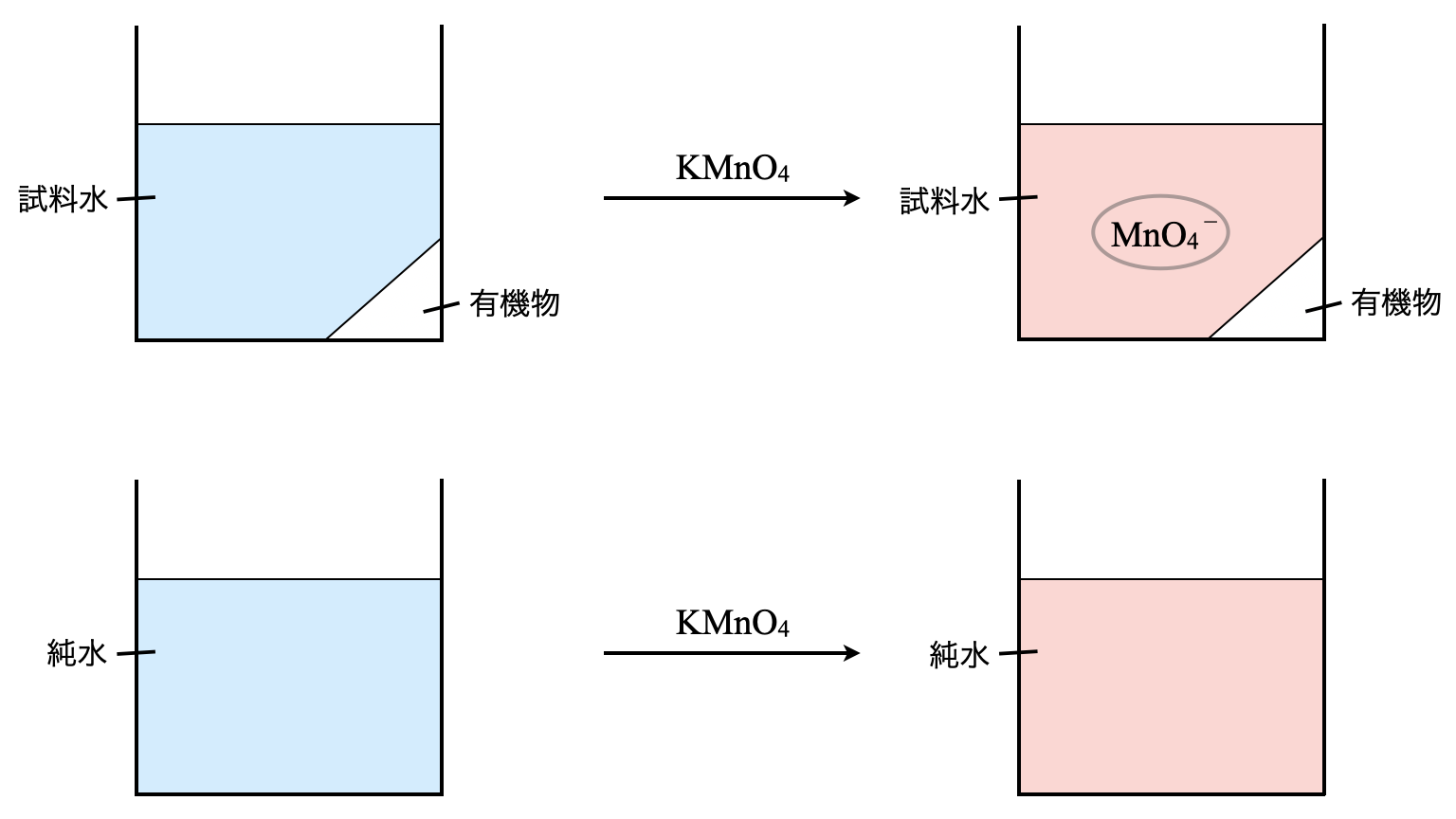
過マンガン酸カリウムを使う理由
\(\rm{COD}\)の意義などは理解していただけたと思いますので,次はより具体的に解説していきます.
その前に\(\rm{COD}\)では過マンガン酸カリウムを利用するので,その理由についても解説しておきましょう.
酸化還元滴定には主に以下の\(2\)種類があります.
- \(\rm{KMnO_4}\)(過マンガン酸)滴定
- ヨウ素滴定
ここでヨウ素滴定は,ヨウ素デンプン反応を用いて滴定を行います.ここで用いるデンプンも有機物です.未知の有機物量を測定するために,追加で有機物を加えたのでは,未知の有機物量を測定することはできませんよね.
そのため,今回はヨウ素滴定ではなく,\(\rm{KMnO_4}\)(過マンガン酸)滴定を用いて,未知の有機物量を測定します.
\(\rm{COD}\)の手順を徹底解説
それでは例題を用いて\(\rm{COD}\)の手順を徹底解説していきましょう.これをしっかりと読んでいただくことで,\(\rm{COD}\)関連の問題は確実に得点することができるようになります!最後までついてきてくださいね!
操作①:ある河川で採取した試料水\(\rm{50\ mL}\)に\(\rm{6.0\ mol/L}\)希硫酸\(\rm{5\ mL}\)を加えて酸性とし,ここへ\(\rm{2.0 × 10^{-3}\ mol/L}\)の\(\rm{KMnO_4}\)水溶液を\(\rm{10\ mL}\)加えて\(30\)分間煮沸する.加熱後,フラスコ中の水溶液は薄い赤紫色に呈色していた.
操作②:熱い間に,\(\rm{5.0 × 10^{-3}\ mol/LNa_2C_2O_4}\)水溶液を\(\rm{10\ mL}\)加える.
操作③:これにビュレットから\(\rm{2.0 × 10^{-3}\ mol/LKMnO_4}\)水溶液を滴下すると,終点までに\(\rm{2.5\ mL}\)要した.
この河川の\(\rm{COD}\)(単位\(\rm{:mg/L}\))を求めよ.
かなりの長文で読むだけで疲れてしまうような問題です.各操作について図を書きながら,わかりやすく解説していきます.
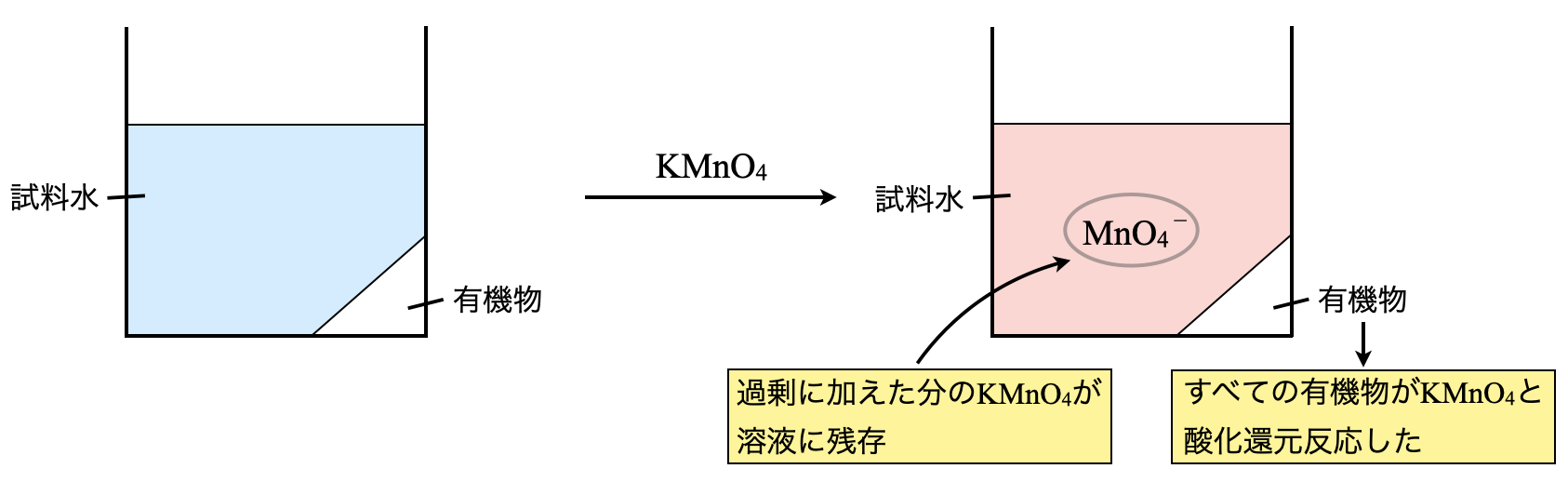
操作①
まずは試料水を\(\rm{KMnO_4}\)水溶液と混合させます.このとき\(\rm{KMnO_4}\)の加えた量が過剰であるため,\(\rm{KMnO_4}\)は一部残存します.
この操作を\(e^-\)の物質量の線分図で書くと,下のようになります.\(\rm{COD}\)は理解が難しいので,操作の図と\(e^-\)の物質量の線分図の\(2\)本立てでいきますよ!
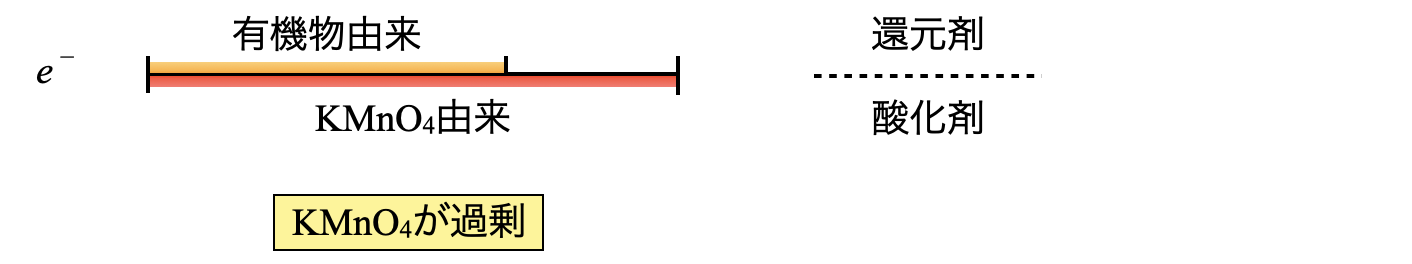
希硫酸を加えた理由についても解説しておきます.
希硫酸を加えたことで,試料溶液は酸性となります.酸性溶液になると,\(\rm{{MnO_4}^-}\)は強力な酸化作用を示して以下のように\(\rm{Mn^{2+}}\)となります.
\(\rm{{MnO_4}^-\ +\ 8H^+\ +\ 5e^-\ →\ Mn^{2+}\ +\ 4H_2O}\)
そのためこの問題に書かれている希硫酸の濃度は計算として使うことはありません.
操作②
次に,\(\rm{Na_2C_2O_4}\)水溶液を加えます.操作①の\(\rm{KMnO_4}\)に加えて,今回の\(\rm{Na_2C_2O_4}\)も過剰に加えています.先ほど残存していた\(\rm{KMnO_4}\)と酸化還元反応し,さらに過剰分が\(\rm{Na_2C_2O_4}\)として残存しているという状態です.
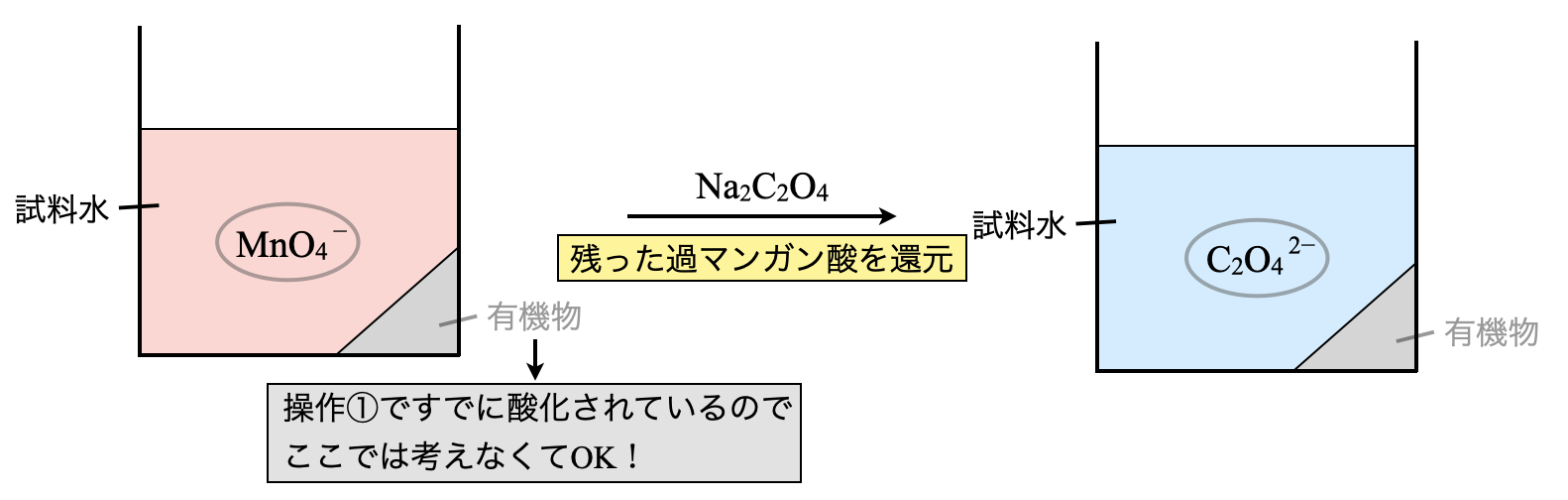
線分図は下のように変化します.

操作①で残存していた\(\rm{{MnO_4}^-}\)とちょうど等しくなる\(\rm{{C_2O_4}^{2-}}\)を加えればいいのに…と思う方が多くいるかもしれません.私も受験生時代は本当にそう思っていました.
ただこれは自分で研究をしだして分かったことなのですが,\(\rm{{MnO_4}^-}\)とちょうど等しくなる\(\rm{{C_2O_4}^{2-}}\)の量というのは正確に求めることができません.そのため\(\rm{{C_2O_4}^{2-}}\)を少し過剰量加えて,それを操作③で滴定していきます.
操作③
ここから操作①と同じ濃度の\(\rm{KMnO_4}\)水溶液をさらに加えていきます.ここでようやく過マンガン酸カリウムのワザである「\(\rm{{MnO_4}^-}\)の赤紫色が残るようになったら滴定終了」を使います.
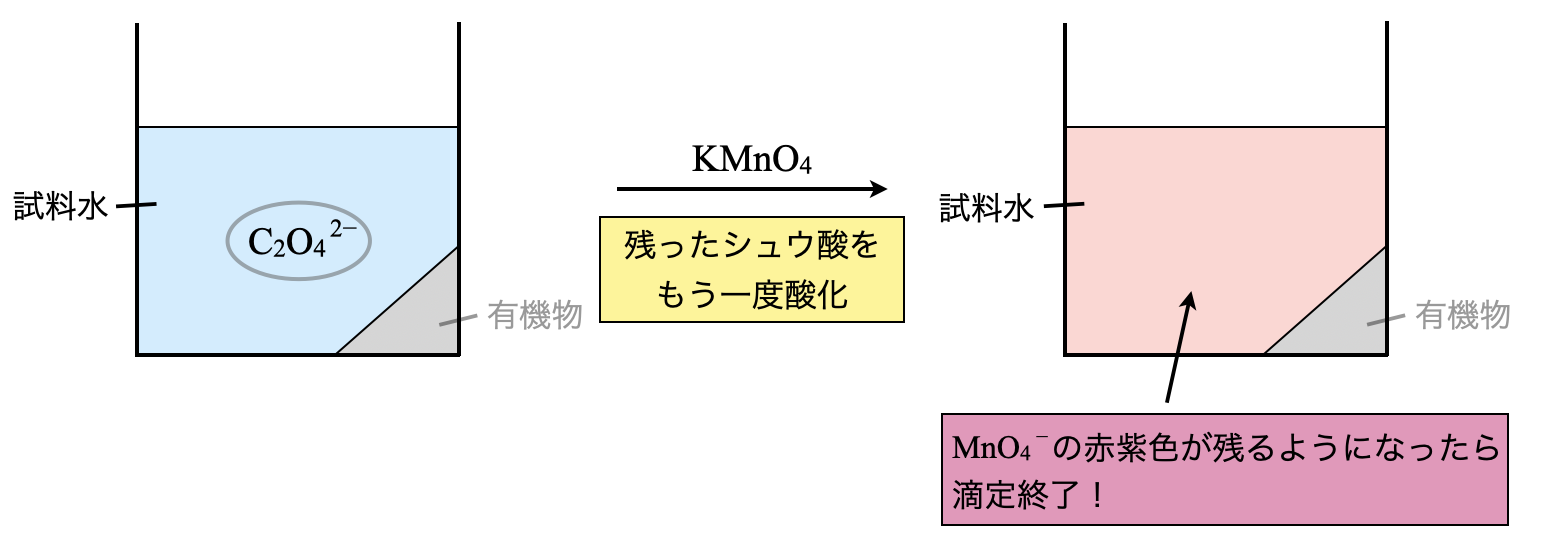
線分図も完成させることができます.

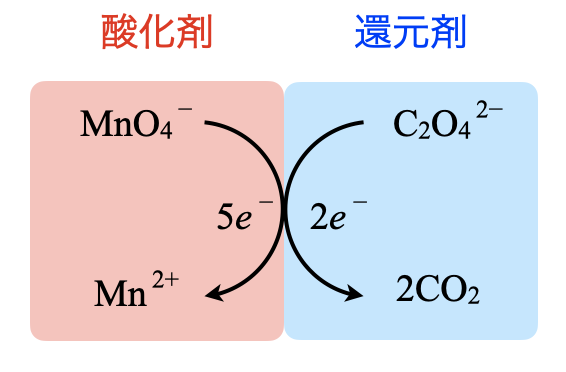
操作①〜③で加えた\(\rm{KMnO_4}\)と\(\rm{Na_2C_2O_4}\)の物質量(モル)は計算で求めることができます.ここからのポイントは,物質間の移動をするときには,\(e^-\)の物質量(モル)を考えるという点です.
物質間を移動して計算するときは,\(e^-\)の物質量(モル)を考えます.さらに,\(e^-\)の物質量(モル)については,
(酸化剤の\(e^-\)) \(=\) (還元剤の\(e^-\))
となり,酸化剤と還元剤の\(e^-\)は必ず等しくなります.
酸化剤と還元剤の\(e^-\)の物質量が等しくなることを数式として表していきます.それぞれの\(e^-\)の物質量を求めるには,下のような図で求めていくと簡単に求めることができます.
操作①〜③で加えた\(\rm{{MnO_4}^-}\),\(\rm{{C_2O_4}^{2-}}\)の物質量を求めていきます.
・\(\rm{{MnO_4}^-}\)
加えた\(\rm{{MnO_4}^-:2.0 × 10^{-3} × (10+2.5) = 0.025\ mmol}\)
\(e^-:0.025 × 5 = 0.125\ \rm{mmol}\)
・\(\rm{{C_2O_4}^{2-}}\)
加えた\(\rm{{C_2O_4}^{2-}:5.0 × 10^{-3} × 10 = 0.050\ mmol}\)
\(e^-:0.050 × 2 = 0.10\ \rm{mmol}\)
この\(2\)つの差である\(\rm{0.025\ mmol}\)が有機物から放出された\(e^-\)の物質量となります.
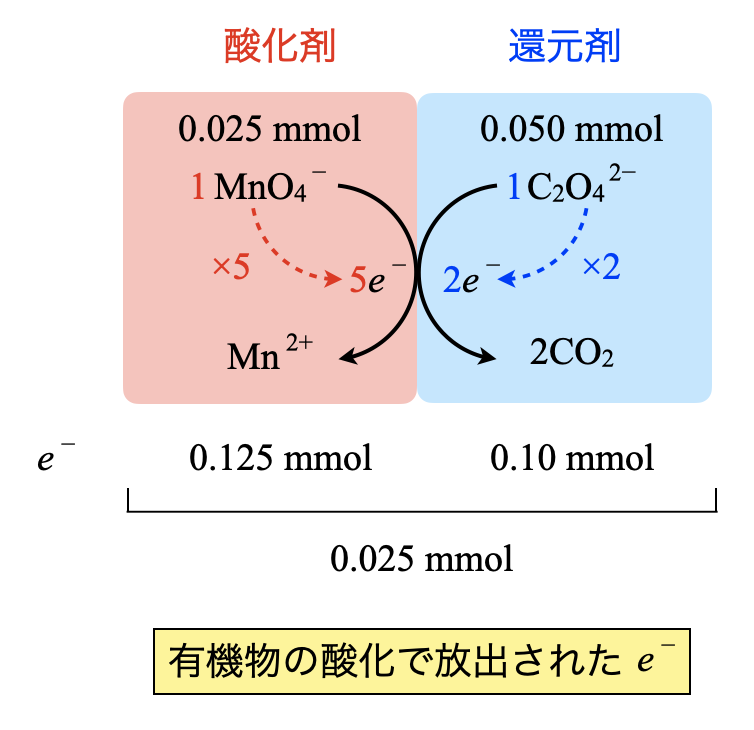
線分図で確認すると,この\(2\)つの物質量の差を考えれば良いことがすぐに理解できると思います!
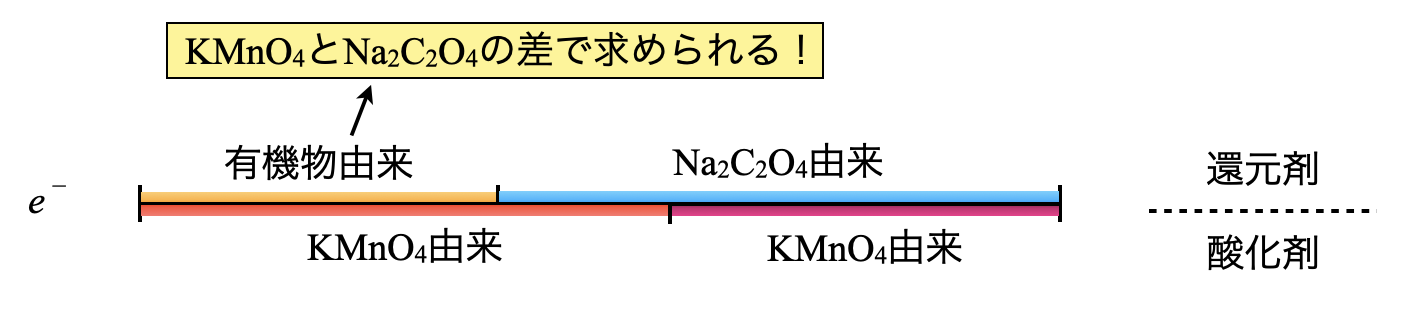
最後は以下の反応を考えることで,\(\rm{O_2}\)の物質量を考え,質量を求めていきます.
\(\rm{O_2\ +\ 2H_2O\ +\ 4e^-\ →\ 4OH^-}\)
\(\rm{O_2}\)の質量\(:\large \frac{0.025\ \rm{mmol}}{4} \small × 32 = 0.20\ \rm{mg}\)
ここで最後の注意ポイントとして,この\(\rm{O_2}\)質量は試料水\(\rm{50\ mL}\)での有機物を\(\rm{O_2}\)に換算した質量であるということです.\(\rm{COD}\)の単位を見ると\(\rm{mg/L}\)であるので,\(\rm{1\ L}\)に換算しましょう.
\(\rm{COD:0.20\ mg × \large \frac{1000}{50} \small = 4.0\ mg}\)
と求めることができます.
非常に長かったので,攻略\(4\)選をまとめておきます!
ポイント\(1:\)線分図を書いて,今回の物質量関係を図示する
ポイント\(\rm{2:{MnO_4}^-}\)と\(\rm{{C_2O_4}^{2-}}\)の物質量の差が有機物から放出された\(e^-\)の物質量となることを見抜く
ポイント\(3:\)有機物から放出された\(e^-\)の物質量から\(\rm{O_2}\)の質量を求める
ポイント\(4:\)最後に今まで計算した値が試料水何\(\rm{mL}\)であるのかを再確認する!
練習問題
今まで解説した\(\rm{COD}\)の手法を用いて,下の練習問題を解いていきましょう.
河川の試料水\(\rm{100\ mL}\)をビーカーに入れ,\(\rm{6\ mol/L}\)硫酸水溶液を\(\rm{10\ mL}\)加え,さらに\(\rm{5.00 × 10^{-3}\ mol/L}\)過マンガン酸カリウム水溶液を\(\rm{10.00\ mL}\)加え,加温した.溶液が熱いうちに\(\rm{12.5 × 10^{-3}\ mol/L}\)シュウ酸水溶液により滴定して,\(\rm{10.0\ mL}\)加えた.このビーカーに\(\rm{5.00 × 10^{-3}\ mol/L}\)過マンガン酸カリウム水溶液を加え,\(\rm{3.05\ mL}\)のとき終点とした.
上の操作とは別に,試料水の代わりに\(\rm{100\ mL}\)の純水を用いて同様の操作を行い,\(\rm{5.00 × 10^{-3}\ mol/L}\)過マンガン酸カリウム水溶液で滴定を行うと,\(\rm{0.05\ mL}\)消費された.
このときの\(\rm{COD(mg/L)}\)を求めよ.
この問題を解く前にブランクテストについて解説しておきましょう.
試料を加えない溶媒に対して,同じ滴定操作を行うことをブランクテスト(空試験)といいます.このブランクテストを行うことで,容器や実験室などの環境要因からの不純物による測定誤差の補正に役立ちます.
実際にこの問題で具体的にブランクテストの意味を解説します.
純水\(\rm{100\ mL}\)を用いて\(\rm{5.00 × 10^{-3}\ mol/LKMnO_4}\)を\(\rm{0.05\ mL}\)消費したということは,試料以外でなにかの物質が一部\(\rm{KMnO_4}\)と反応したよ,ということです.つまり,先ほどの操作で使用した\(\rm{3.05\ mL}\)のうち\(\rm{0.05\ mL}\)は本反応とは関係のない物質が一部反応してしまったということです.
そのため,この分を除いて考える必要があり,問題を書き換えると下のようになります.
このときの\(\rm{COD(mg/L)}\)を求めよ.
これで先ほどと同じ問題となりました.順に解いていきましょう!
ポイント\(1:\)線分図を書いて,今回の物質量関係を図示する
今回の問題を線分図に書いていきましょう.

ポイント\(\rm{2:{MnO_4}^-}\)と\(\rm{{C_2O_4}^{2-}}\)の物質量の差が有機物から放出された\(e^-\)の物質量となることを見抜く
先ほどの図から,\(\rm{{MnO_4}^-}\)と\(\rm{{C_2O_4}^{2-}}\)の物質量の差が有機物から放出された\(e^-\)の物質量になることは一目でわかると思います.それでは実際に計算していきましょう.
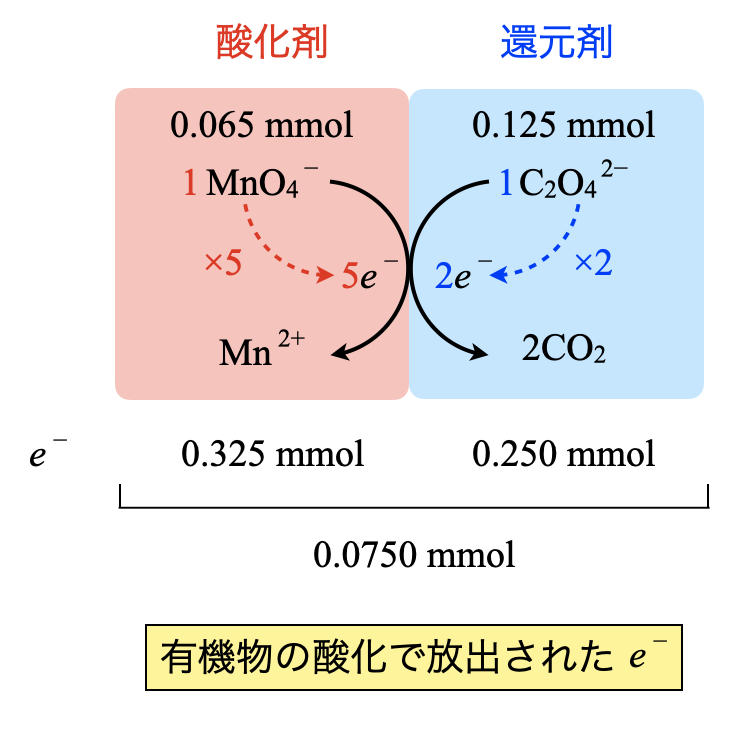
・\(\rm{{MnO_4}^-}\)
加えた\(\rm{{MnO_4}^-:5.00 × 10^{-3} × (10.00 + 3.00) = 0.065\ mmol}\)
\(e^-:0.065 × 5 = 0.325\ \rm{mmol}\)
・\(\rm{{C_2O_4}^{2-}}\)
加えた\(\rm{{C_2O_4}^{2-}:12.5 × 10^{-3} × 10.0 = 0.125\ mmol\ mmol}\)
\(e^-:0.125 × 2 = 0.250\ \rm{mmol}\)
そしてこの差\(\rm{0.325 – 0.250 = 0.0750\ mmol}\)が有機物から放出された\(e^-\)の物質量となります.
ポイント\(3:\)有機物から放出された\(e^-\)の物質量から\(\rm{O_2}\)の質量を求める
さらに以下の反応式から\(\rm{O_2}\)の物質量→質量の順に求めていきます.
\(\rm{O_2 + 4H^+ + 4e^- → 2H_2O}\)
\(\rm{O_2}\)の質量\(\rm{:\large \frac{0.075\ mmol}{4} \small × 32.0 = 0.6\ mg}\)
ポイント\(4:\)最後に今まで計算した値が試料水何\(\rm{mL}\)であるのかを再確認する!
最後にこの試料\(\rm{100\ mL}\)あたりの\(\rm{O_2}\)質量が\(\rm{0.6\ mg}\)なので,\(\rm{1\ L}\)に換算する必要があります.
\(\rm{COD = 0.6 × 10 = 6.0\ mg/L}\)
今回はここまでとなります.とてもボリュームのある分野なので大変だったかもしれませんが,\(\rm{COD}\)の問題は\(4\)ステップで完全攻略できることが分かったと思います!あとは練習あるのみです.そんなに問題パターンがあるわけではないので,\(1\)問を完全に理解して得点に繋げていきましょう!



コメント