このような疑問をしっかりと解決していきます!
本記事では,まずは緩衝溶液について基礎的な内容を理解したあと,計算問題も解けるように解説していきます!
それでは今日も最後まで一緒に頑張りましょう!!
緩衝溶液
緩衝溶液
まず,緩衝溶液について理解していきましょう!
弱酸や弱塩基の溶液に酸や塩基を加えても水溶液のpHが変化せずにほぼ一定に保つ働きがあります.
これを緩衝作用といい,そのような状態の溶液を緩衝溶液といいます.
ここでのポイントは,
酸や塩基を加えても水溶液のpHがほとんど変化しないということです.
図で表すと,下のような状態のことを言います.
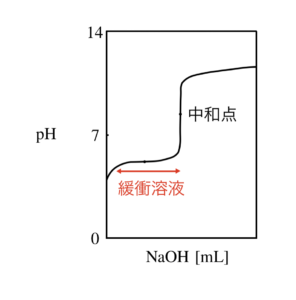
緩衝溶液の原理
では,緩衝溶液の原理について理解していきましょう!
例として,弱酸のCH3COOH(以下,AHとする)とCH3COONa(以下,ANaとする)の溶液は以下の電離平衡が存在しています.
AH ⇄ A– + H+
ANaはA–とNa+に完全に電離しており,AHが平衡状態となっています.
では,この溶液にそれぞれの物質を加えたときにどのような変化が起こるのかを見ていきましょう!
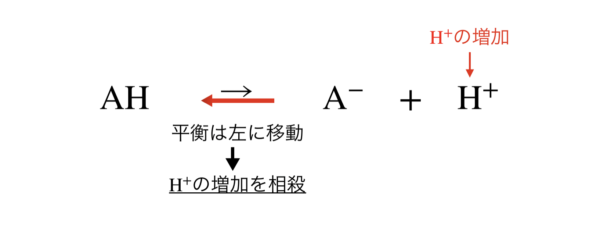
強酸を加えたとき,[H+]が増加しますが,ル・シャトリエの原理により,[H+]が減少する方向に平衡が移動します.
つまり,この場合は左に移動し,[H+]の増加は相殺されます.
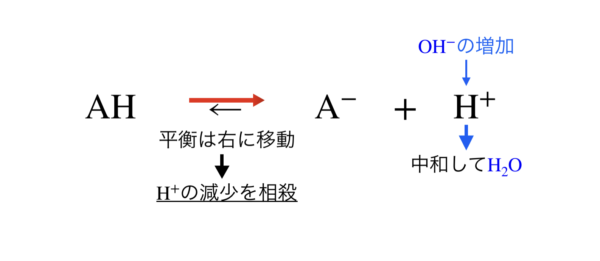
一方,強塩基を加えたとき,[OH–]が増加しますが,[H+]と中和反応し,[H+]が減少します.
そこでル・シャトリエの原理により,反応が右に移動し,[H+]の減少が相殺されます.
つまり,強酸・強塩基いずれを加えたときも[H+]の濃度がほぼ一定に保たれます.
次に,AHにA–Na+を加える理由について考えてみましょう!
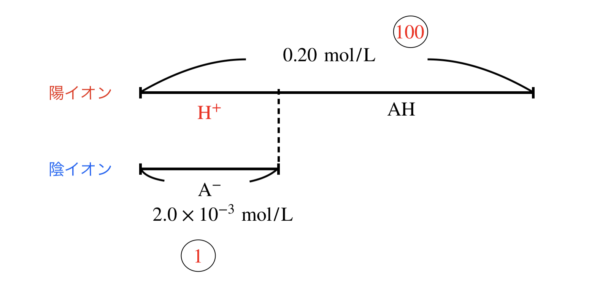
AHのモル濃度が\(0.20\ \rm{mol/L},\rm{AH}\)の\(K_{\rm{a}} = 2.0 × 10^{-5}\ \rm{mol/L}\)とします.
近似解を用いると,\([\rm{H}^+] = \sqrt{0.20 × 2.0 × 10^{-5}} = 2.0 × 10^{-3}\ \rm{mol/L}\)
となります.
全体:\([\rm{H}^+] = 0.20 : 2.0 × 10^{-3} = 100 : 1\)
となり,この溶液は以下の状態になっています.
では,この溶液に強酸を加えてみましょう!
ル・シャトリエの原理により,平衡が左に移動するため,このままではA–が不足してしまいます.
この不足を補うために,A–を過剰に加えておく必要があります.
このA–はA–Na+由来のものであるため,A–Na+を事前に加えておくのです!
緩衝溶液の[H+]計算
では,緩衝溶液の[H+]の計算方法を学んでいきましょう!
問題として,以下のような状況を考えてみましょう!
\(\rm{CH_3COOH}\)の平衡定数を\(K_{\rm{a}}\)とする.
まず,\(\rm{CH_3COONa}\)については次のように完全に電離しています.
CH3COONa → CH3COO– + Na+
完全電離しているので,\([\rm{CH_3COO}^-] =\ \)\(C^{’}\ \rm{mol/L}\)となります.
次に,\(\rm{CH_3COOH}\)の電離について考えていきましょう.
CH3COOH ⇄ CH3COO– + H+
平衡が左に\(x\ \rm{mol/L}\)移動するとすると,下のようになります.
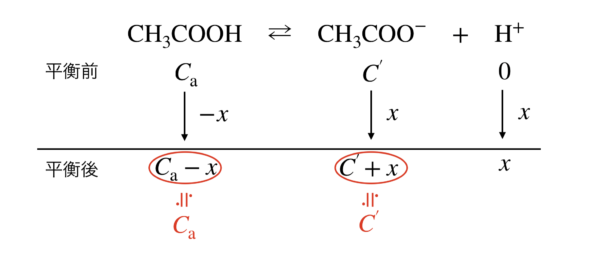
これを見ると,
\([\rm{CH_3COOH}] =\ \)\(C_{\rm{a}} – x\ \rm{mol/L}\),\([\rm{CH_3COO}^-] =\ \)\(C^{’} + x\ \rm{mol/L}\)となりますが,近似すると,
\([\rm{CH_3COOH}] ≒\ \)\(C_{\rm{a}}\ \rm{mol/L},[\rm{CH_3COO}^-] ≒\ \)\(C^{’}\ \rm{mol/L}\)となります.
この理由を考えてみましょう!
\(\rm{CH_3COOH}\)のみの溶液であれば,
\([\rm{CH_3COOH}] =\ \)\( C_{\rm{a}} – x\ \rm{mol/L}\),\([\rm{CH_3COO}^-] =\ \)\(C^{’} + x\ \rm{mol/L}\)のままとなります.
しかしながら,この溶液には\(C^{’}\ \rm{mol/L}\)の\(\rm{CH_3COONa}\)が含まれているので,
\(\rm{CH_3COO}^-\)が増加し,平衡が左に移動します.
すると,最初は右に平衡が移動したのに,左に平衡が移動してしまうので,平衡移動が相殺されます.
そのため,今回は\(C_{\rm{a}} >> x,C^{’} >> x\)となるので,近似できるというわけです!
この辺りの理屈は少し難しいですが,緩衝溶液では大切な部分なので何度も復習して理解しておきましょう!
次に,平衡定数\(K_{\rm{a}}\)を用います.
このまま,濃度を使用してもいいですが,ここでは物質量(モル)で考えていきましょう.
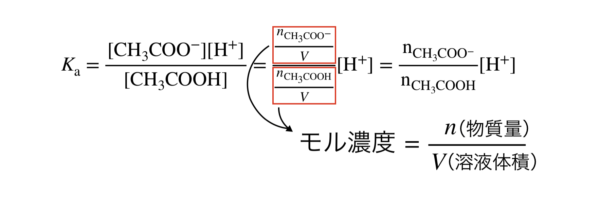
なぜかというと,\(\rm{CH_3COOH}\)と\(\rm{CH_3COONa}\)を加えているため,溶液の混合で濃度が変化してしまうからです.
濃度には,このように「希釈」という考えを追加して考えなくてはいけません.
これではめんどくさいので,物質量(モル)で考えると必ず変化しないので,ラクになりますよ.
本日はここまでです!
今日は,緩衝溶液の計算では物質量(モル)を用いて計算するということを確実に覚えてください!
次回は,緩衝溶液の実践的な問題演習を行い,実際にどのように物質量(モル)を用いて解くのか解説していきますね!
緩衝溶液は非常に難しい分野で入試でも頻出なので,必ず解けるようにしておきましょう!
学生の頃,本当に緩衝溶液がわからず,参考書やネットを読み漁った記憶があります……



コメント