このような疑問をしっかりと解決していきます!
本記事では,まず[H+]計算を図を使って確実に解けるようにします.
また,近似計算ができるときとできないときの見分け方もしっかりと解説していきます!
近似計算…?という方もいると思いますが,この記事を見ていただくだけで,しっかりと意識しながら問題を解けるようになりますよ!
[H+]計算の分類
まず初めに[H+]計算の分類を紹介していきます.
全体像がわかってから,それぞれの解き方について詳しく解説していきます!
今回のテーマは3回くらいと長くなると思うので,自分のペースでゆっくりと進んでいってください!
まず[H+]を求めるには,近似解と厳密解の求め方があります.
また酸には強酸と弱酸(1価),弱酸(2価)があります.
これらをまとめると,下の図のようになります.
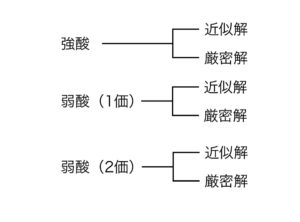
それぞれの酸について近似解と厳密解があるということです.
これを踏まえた上で,それぞれの解法について基礎的な部分からしっかりとおさえていきましょう!
今日は,まず強酸について学習していきます!
強酸
強酸(近似解)
近似解を使う問題を考えていきましょう!
この問題が基本的でみなさんもこの解法で解いている方が多いと思いますが,注意点もありますのでしっかりと読んでくださいね!
強酸の場合は,溶液中の\( [\rm{H}^+]\)がどの値になるかを考えてください!
下の図の\(\rm{pH} = 6 \)〜\(8\)に入る溶液では,近似解は使えず,水の電離を考慮した厳密解を使わなければなりません.
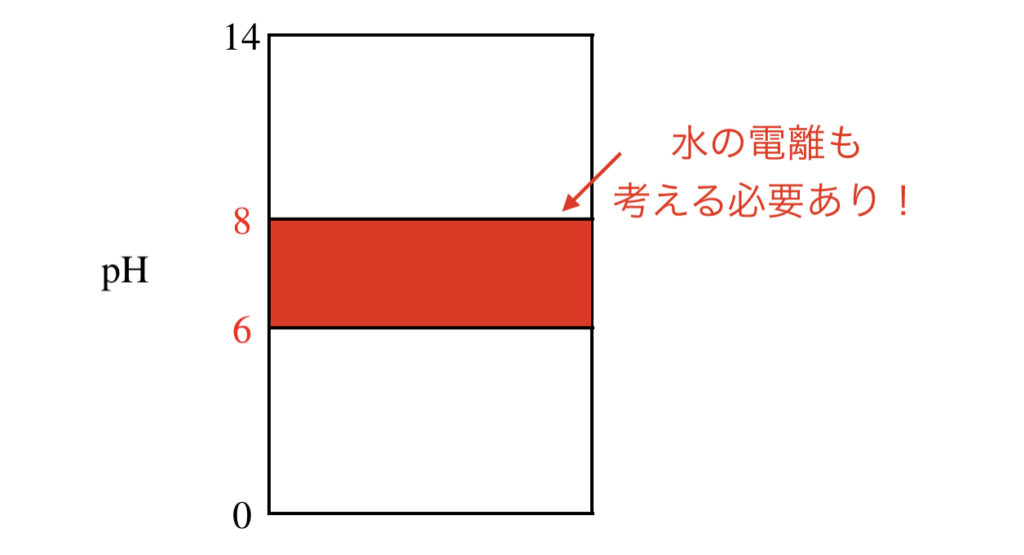
今回の溶液は,\( [\rm{H}^+] = 1.0 × 10^{-4}\ \rm{mol/L} \)なので,近似解が使えますね!
そのため,これが答えとなります.
強酸(厳密解)
では,次のような溶液を考えてみましょう!
この溶液は近似解で計算すると,\([\rm{H}^+] = 2.0 × 10^{-7}\ \rm{mol/L} \)となるので,水の電離を考慮した厳密解を使わなければりません.
\([\rm{H}^+] =\) \(x\ \rm{mol/L}\)とすると,\([\rm{OH}^-] = \) \(x-2.0×10^{-7}\ \rm{mol/L}\)となり,下の図のようになります.
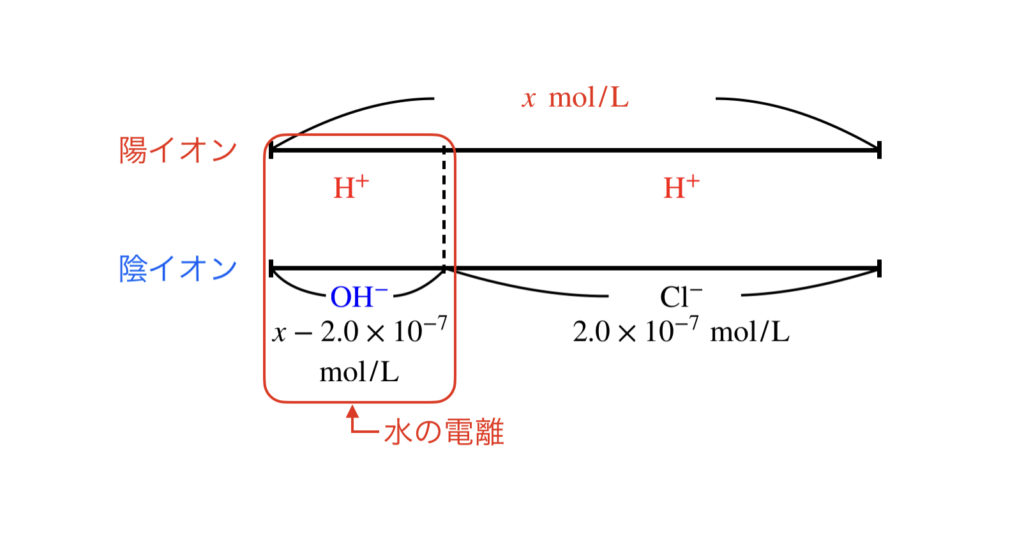
これらの値を水のイオン積:\( K_{\rm{w}} = [\rm{H}^+][\rm{OH}^-] \)に代入すると,
\( K_{\rm{w}} = x × ( x – 2.0 × 10^{-7}) = 1.0 × 10^{-14} \)
これを解くと,
\( x = ( 1 + \sqrt{2}) × 10^{-7}\ \rm{mol/L}\)
となります.
強酸についてまとめると,下のようになります.
まとめ
本日のまとめは以下のようになります.
これを実際の問題で使えるように何度も練習して下さい!
次回は,弱酸について紹介していきます!
今日はお疲れ様でした!


コメント