
- 滴定曲線の捉え方
- 弱酸+強塩基の一連の流れ
を特にポイントとしています.昨日の自分より少しでもレベルアップしていきましょう!
解説してほしい分野があればぜひ次の記事のコメント欄で教えてくださいね!

なぜ弱酸+強塩基がテストで頻出なのか?
今回は弱酸+強塩基について徹底的に解説していきます.この記事を読み終わるころには,確実に解き方を理解していただけると思います!最後までついてきてくださいね!
一般的に考えても難しくなるだけなので,具体的に考えていきましょう.
テストで頻出なのは,弱酸として酢酸(\(\rm{CH_3COOH}\)),強塩基として水酸化ナトリウム(\(\rm{NaOH}\))というパターンです.このパターンさえ確実に理解しておけば,他のパターンが出たときにも対応できるようになりますよ!
まず初めに,皆さんの中にはなぜこの弱酸+強塩基のパターンがテストでよく出るのか?と疑問に思ったことはありませんか?私が受験生の頃には,難しそうだからかな…?となんとなくしか考えていませんでした.
ただ,この弱酸+強塩基のパターンには緩衝溶液や加水分解など勉強になるパターンが全て詰まっています.そのためしっかりと勉強しているかどうかを見極めるにはうってつけの問題というわけです.
それではこの問題の意義を理解した上で,\(1\)つずつ攻略していきましょう!
滴定曲線の捉え方
以下の問題を考えていきます.
\(C\ \rm{[mol/L]}\)の酢酸\(\rm{CH_3COOH}\)水溶液\(V \rm{[mL]}\)に,\(C\ \rm{[mol/L]}\)の水酸化ナトリウム\(\rm{NaOH}\)水溶液を滴下していく.\(\rm{CH_3COOH}\)は水溶液中で一部が電離し,その電離平衡および電離定数\(K_{\rm{a}}\)は以下のように表される.
\(\rm{CH_3COOH\ ⇄\ CH_3COO^-\ +\ H^+}\),\(K_{\rm{a}} = \large \rm{\frac{[CH_3COO^-][H^+]}{[CH_3COOH]}}\)
(\(1\))\(\rm{NaOH}\)水溶液を滴下する前の\(\rm{[H^+]}\)を求めよ.
(\(2\))(\(1\))の水溶液に\(\rm{NaOH}\)水溶液を\(\large \frac{1}{2} \small V\ \rm{[mL]}\)加えたときの\(\rm{[H^+]}\)を求めよ.
(\(3\))(\(2\))の水溶液にさらに\(\rm{NaOH}\)水溶液を\(\large \frac{1}{2} \small V\ \rm{[mL]}\)加えたときの\(\rm{[OH^-]}\)を求めよ.
(\(4\))(\(3\))の水溶液にさらに\(\rm{NaOH}\)水溶液を\(\large \frac{1}{2} \small V\ \rm{[mL]}\)加えたときの\(\rm{[OH^-]}\)を求めよ.
まずこの問題の流れを滴定曲線で考えていきます.中和滴定を考えるときには,滴定曲線を描き,今自分がどの位置にいるのかをしっかりと見極めることが大切となります.
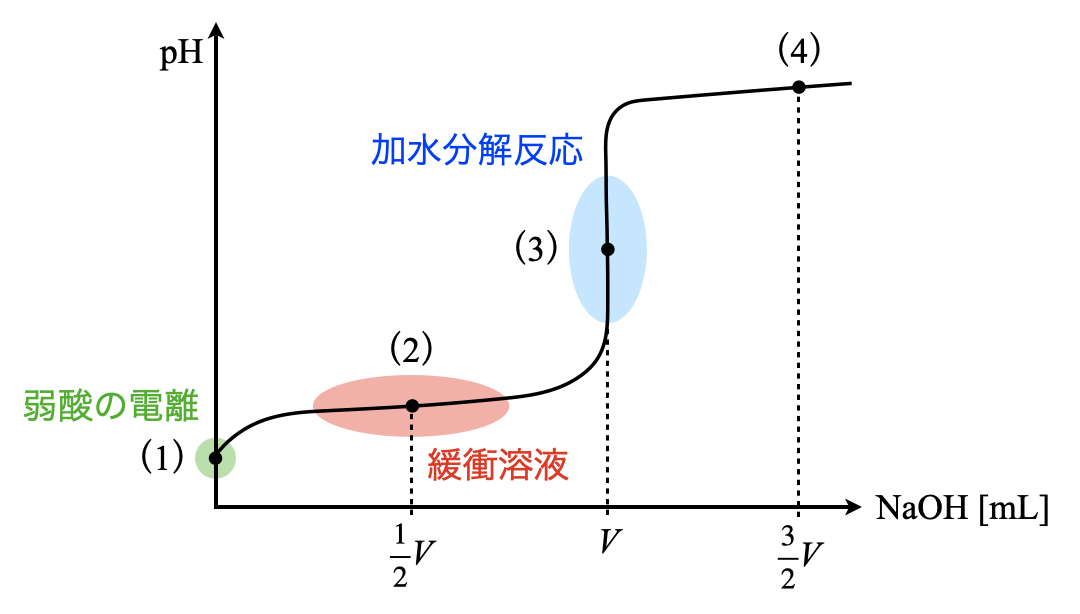
図を見ると,弱酸しかなければ弱酸の電離(\(1\)),その溶液に少しずつ\(\rm{NaOH}\)水溶液を加えていったときに緩衝溶液(\(2\)),中和点が加水分解反応(\(3\))であることが一発でわかると思います!これが滴定曲線を書くことの威力ですよ!
弱酸の\(\rm{[H^+]}\)計算
(\(1\))は\(C\ \rm{[mol/L]}\)の\(\rm{CH_3COOH}\)水溶液なので,弱酸の電離に関する問題となります.弱酸の電離は基本的な内容ですが,丁寧に解説していきますね!
\(\rm{CH_3COOH}\)の電離度を\(\alpha\)とすると,平衡時のモル濃度はそれぞれ以下のようになります.
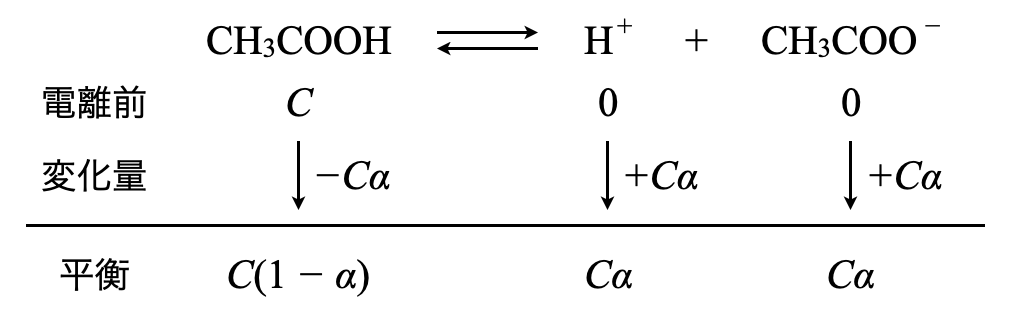
これを電離定数\(K_{\rm{a}}\)に代入していきます.
\(K_{\rm{a}} = \large \frac{C\alpha\ ×\ C\alpha}{C(1\ -\ \alpha)} \small = \large \frac{C\alpha^2}{1\ -\ \alpha}\)
ここで,近似できるかどうかが\(1\)つのポイントとなります.それぞれ\(2\)つに分けて解説していきます.
弱酸の近似解
近似できるということは,\(1 – \alpha ≒ 1\)とできるということです.これは\(1 >> \alpha\)であるということと同じ意味になります.このポイントを見逃してすぐに近似解を使おうとする人がいるので注意してくださいね!
すると,
\(K_{\rm{a}} ≒ C\alpha^2\)より,\(\alpha = \sqrt{\large \frac{K_{\rm{a}}}{C}}\)
この\(K_{\rm{a}}\)の値を\(\rm{H^+}\)に代入すると,\(\rm{[H^+]}\)を求めることができます.
\({\rm{[H^+]}} = C\alpha = C × \sqrt{\large \frac{K_{\rm{a}}}{C}} = \sqrt{CK_{\rm{a}}}\)
一般的には,この近似解を求めることで解答して問題ありません.今回の問題も近似解で大丈夫です.ただし,厳密解が必要な場面もあるため,次で紹介しておきます.
弱酸の厳密解
厳密解で考えるということは,\(1 – \alpha\)を\(1\)とは考えられないということです.そのため,\(K_{\rm{a}} = \large \frac{C\alpha^2}{1\ -\ \alpha}\)を\(\alpha\)の\(2\)次方程式として考えていきます.
\(C\alpha^2 + K_{\rm{a}} \alpha – K_{\rm{a}} = 0\)
\(\alpha = \large \frac{-K_{\rm{a}}\ +\ \sqrt{{K_{\rm{a}}}^2+4CK_{\rm{a}}}}{2C}\)
この\(\alpha\)を代入することで,\(\rm{[H^+]}\)を求めることができます.
ところで,この近似解と厳密解はどのように使い分ければよいのでしょうか?以下の\(2\)つのポイントで見極めるようにしてください!
① 問題文に\(\alpha\)が\(1\)より十分に小さいと書かれているとき→近似解
② 最初の濃度に対して\(\rm{[H^+]}\)が\(5\%\)以下のとき→近似解
③ それ以外→厳密解
②だけひっかかると思うので解説しておきます.最初の濃度に対して\(\rm{[H^+]}\)が\(5\%\)以下ということは,平衡が左に\(5\%\)以下しか進んでいない(\(\alpha\)が\(0.05\)以下)ということです.これはほとんど電離していないと考えることができるので,近似解を使えるというわけです.
難関大ではたまに近似解を求められるので,注意しておきましょう!
緩衝溶液の\(\rm{[H^+]}\)計算
(\(2\))は\(C\ \rm{[mol/L]}\)の\(\rm{CH_3COOH}\)水溶液\(V\ \rm{[mL]}\)に\(\rm{NaOH}\)水溶液を\(\large \frac{1}{2} \small V\ \rm{[mL]}\)加えた状態なので,緩衝溶液となっています.緩衝溶液は苦手な受験生が多いので,逆に得点源にしていきましょう!
まず状況確認からしていきます.
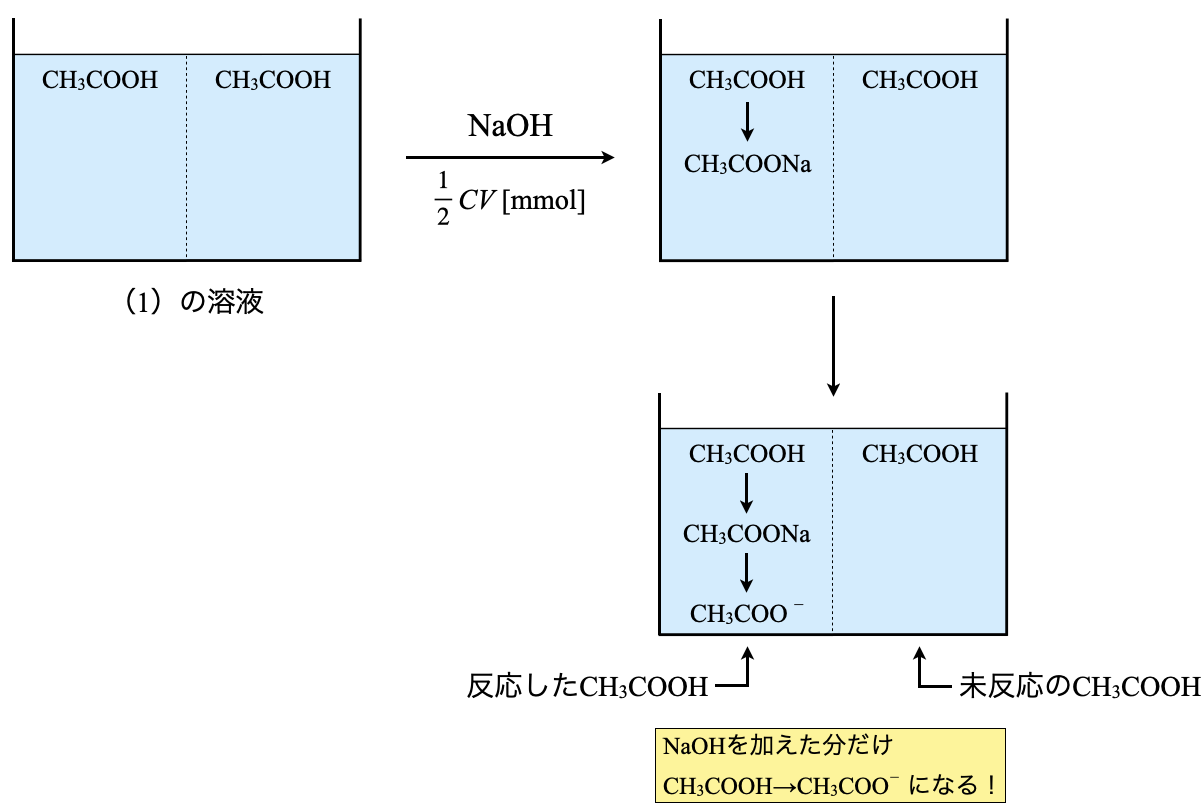
\(\rm{CH_3COOH}\)が入っている水溶液に\(\rm{NaOH}\)を滴下していきます.すると,\(\rm{CH_3COOH}\)と\(\rm{NaOH}\)が以下のように反応します.
\(\rm{CH_3COOH\ +\ NaOH\ →\ CH_3COONa\ +\ H_2O}\)
そのためこの溶液中には,反応した\(\rm{CH_3COONa}\)と未反応の\(\rm{CH_3COOH}\)が存在していることになります.
そしてそれぞれ以下のように電離しています.
反応した\(\rm{CH_3COONa:CH_3COONa\ →\ Na^+\ +\ {CH_3COO}^-}\)
未反応の\(\rm{CH_3COOH:CH_3COOH\ ⇄\ H^+\ +\ {CH_3COO}^-}\)
\(\rm{CH_3COONa}\)に関しては完全に電離して\(\rm{CH_3COO^-}\)が生じている状態になります.そのため溶液中に十分\(\rm{CH_3COO^-}\)が存在している状態になるため,未反応の\(\rm{CH_3COOH}\)の平衡に関しては右方向への変化は十分に抑えられます.結果として,\(\rm{CH_3COOH}\)はそのほとんどが\(\rm{CH_3COOH}\)分子の状態で存在しています.
ここまでの考え方をまとめましょう.毎回上のように考えていては時間がなくなってしまうので,自分でしっかりと整理してすぐに解答できるようにしておく必要があります.
加えた\(\rm{NaOH}\)の物質量分だけ\(\rm{CH_3COO^-}\)が存在する.その残り分が\(\rm{CH_3COOH}\)の物質量となる.
この\(2\)つの物質量の関係を滴定曲線上で表すと下のようになります.
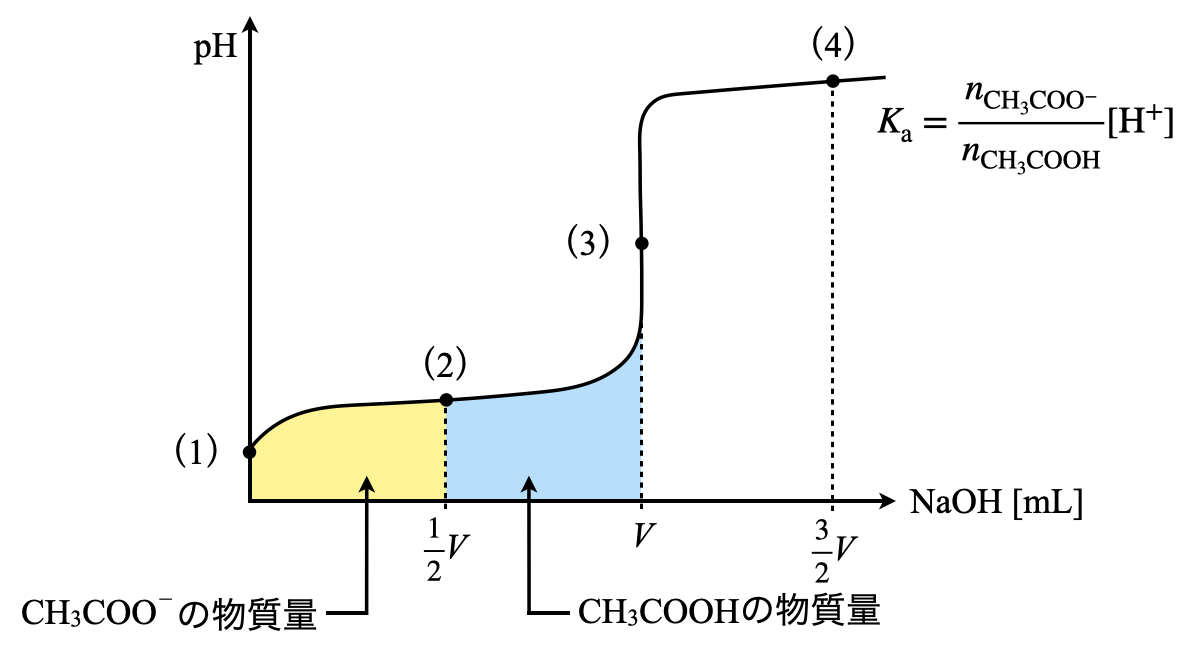
このように表すと,加えた\(\rm{NaOH}\)の物質量分だけ\(\rm{CH_3COO^-}\)が存在しているということを視覚的に捉えやすくなります.これに加えて,\(K_{\rm{a}}\)を考えるときに,物質量を考えるようにしてください!
\(K_{\rm{a}} = \large {\rm{\frac{[CH_3COO^-][H^+]}{[CH_3COOH]}}} \small = \large \frac{n_{\rm{CH_3COO^-}}}{n_{\rm{CH_3COOH}}} \small \rm{[H^+]}\)
この考え方はとても大切です.以下の記事でも解説しているので,見てみてくださいね!

今回の場合,\(n_{\rm{CH_3COO^-}} = n_{\rm{CH_3COOH}} = \large \frac{1}{2} \small CV\ \rm{[mmol]}\)なので,\({\rm{[H^+]}} = K_{\rm{a}}\)となります.
加水分解反応の\(\rm{[OH^-]}\)計算
(\(3\))は(\(2\))の水溶液にさらに\(\rm{NaOH}\)水溶液を加えてちょうど中和した点となります.未反応の\(\rm{CH_3COOH}\)が先ほどと同じように\(\rm{NaOH}\)と以下のような反応をします.
未反応の\(\rm{CH_3COOH:CH_3COOH\ +\ NaOH\ →\ CH_3COONa\ +\ H_2O}\)
そしてこの\(\rm{CH_3COONa}\)は先ほど説明したように\(\rm{CH_3COO^-}\)に電離します.
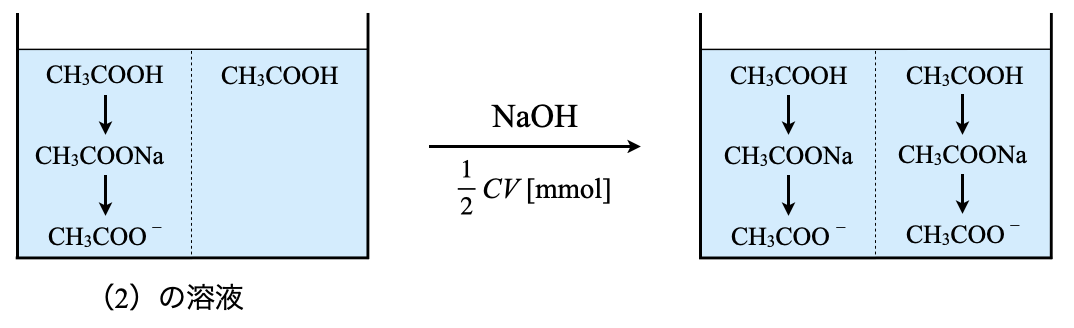
そして生成した\(\rm{CH_3COO^-}\)は以下のように加水分解し,\(\rm{OH^-}\)が生成するので溶液は塩基性になります.
\(\rm{CH_3COO^-\ +\ H_2O\ ⇄\ CH_3COOH\ +\ OH^-}\)
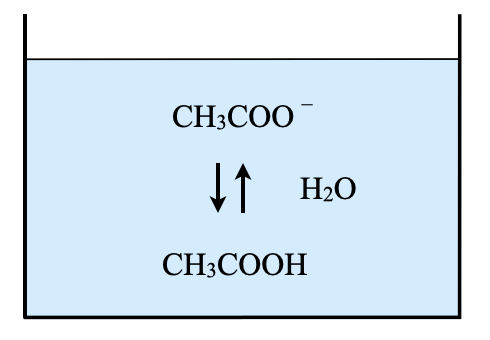
そしてこの加水分解反応の平衡定数を\(K_{\rm{h}}\)とすると,以下のようになります.
\(K_{\rm{h}} = \large \rm{\frac{[CH_3COOH][OH^-]}{[CH_3COO^-]}}\)
この\(K_{\rm{h}}\)は一般的に問題で与えられていないため,自分で求める必要があります.\(K_{\rm{a}}\)と\(K_{\rm{h}}\)をかけてみましょう.
\(K_{\rm{a}} × K_{\rm{h}} = \large {\rm{\frac{[CH_3COO^-][H^+]}{[CH_3COOH]} \small × \large \frac{[CH_3COOH][OH^-]}{[CH_3COO^-]} \small = [H^+][OH^-]}} \small = K_{\rm{w}}\)
\(K_{\rm{h}} = \large \frac{K_{\rm{w}}}{K_{\rm{a}}}\)
とすることで,\(K_{\rm{h}}\)を求めることができます.
\(K_{\rm{a}} × K_{\rm{h}} = K_{\rm{w}}\)
ここまで準備ができたところで,\(\rm{[OH^-]}\)を求めていきます.\(\rm{[OH^-]}\)については以下の記事で解説しています.

\({\rm{[OH^-]}} = \sqrt{C_{\rm{s}}K_{\rm{h}}}\)
ここでの注意点は,\(\rm{[OH^-]}\)を求めるときの\(C_{\rm{s}}\)は\(\rm{CH_3COONa}\)の濃度であるという点です.
今回の問題に当てはめて考えると,\(C_{\rm{s}} = \large \frac{1}{2} \small C\ \rm{[mol/L]}\)です.そのため,\(\rm{[OH^-]}\)は以下のようになります.
\({\rm{[OH^-]}} = \sqrt{C_{\rm{s}}K_{\rm{h}}} = \sqrt{\large \frac{1}{2} \small C × \large \frac{K_{\rm{w}}}{K_{\rm{a}}}}\)
塩基が過剰の場合の\(\rm{[OH^-]}\)計算
(\(4\))は(\(3\))の水溶液にさらに\(\rm{NaOH}\)水溶液を\(\large \frac{1}{2} \small V\ \rm{[mL]}\)加えた点となります.さらに加えた\(\rm{NaOH}\)は他に反応するものがないため,完全電離します.
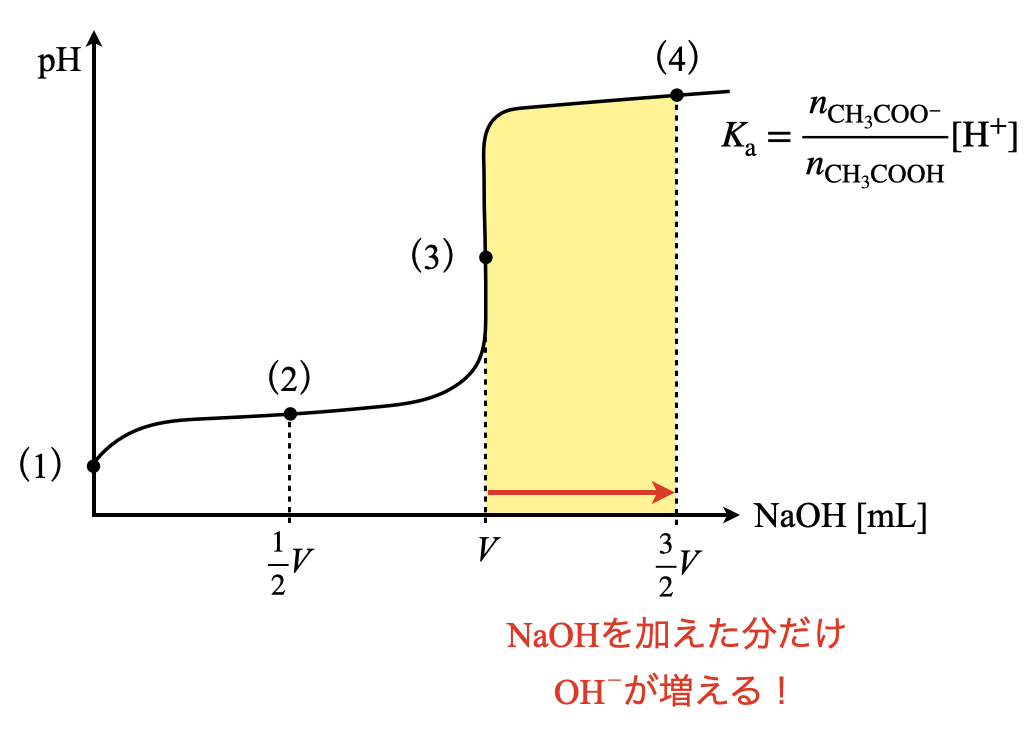
\({\rm{OH^-}}:\large \frac{1}{2} \small CV\ \rm{[mmol]}\)
溶液量\(:V + \large \frac{3}{2} \small V = \large \frac{5}{2} \small V\ \rm{[mL]}\)
よって,
\({\rm{[OH^-]}} = \large \frac{\frac{1}{2}CV}{\frac{5}{2}V} \small = \large \frac{1}{5} \small C\ \rm{[mol/L]}\)
ここまでが弱酸と強塩基の基本的な問題パターンになります.これを攻略するだけで短時間で問題を解答できるようになります.最後に,もう少し難易度の高い問題を\(1\)題だけ解説します.この問題を解くことで,滴定曲線を使うことの威力を知ることができると思います.
(\(5\))(\(1\))の溶液について,\(\rm{NaOH}\)水溶液を\(\rm{20\ mL}\)加えたとき,\(\rm{pH}\)はいくらになるか?
\(C = 0.20\ \rm{mol/L}\),\(V = 30\ \rm{mL}\),\(K_{\rm{a}} = 2.0 × 10^{-5}\ \rm{mol/L}\)とする.
これが最後の問題なので,しっかりとついてきてくださいね!なにわともあれまずは滴定曲線を書いていきましょう!これが滴定を考える上での私たちの羅針盤となります.笑
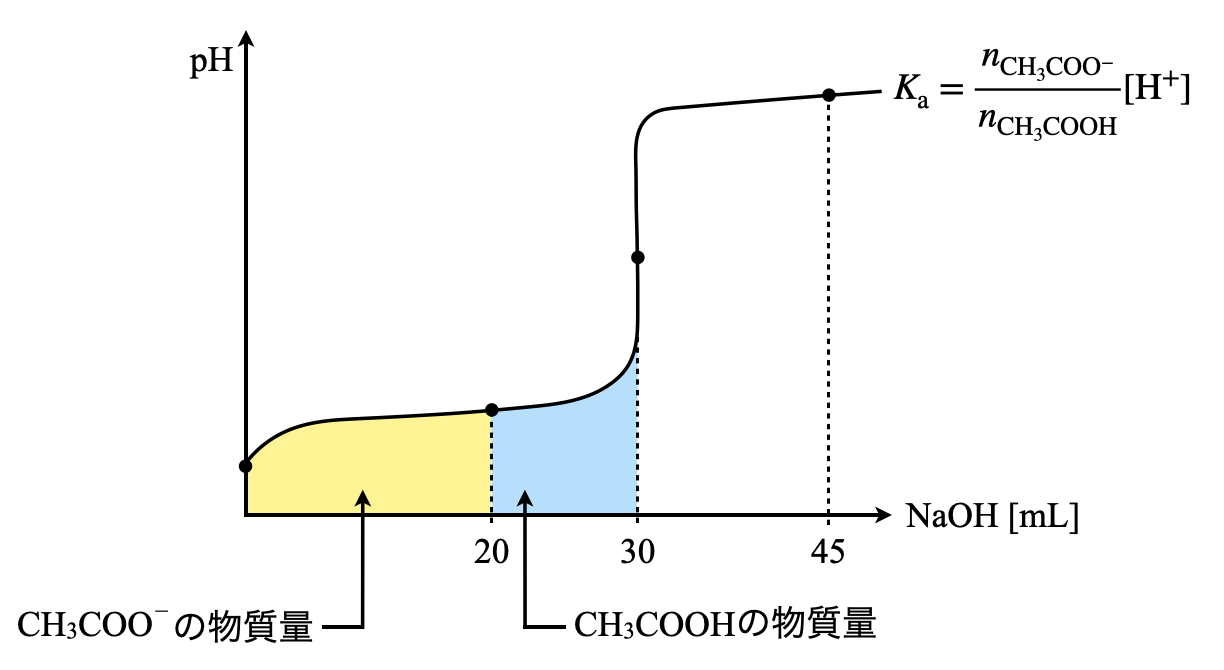
\(V = 30\ \rm{mL}\)に対して,\(\rm{NaOH}\)を\(\rm{20\ mL}\)加えた状態なので,
反応した\(\rm{CH_3COO^-:0.20 × 20 = 4.0\ mmol}\)
未反応の\(\rm{CH_3COOH:0.20 × 10 = 2.0\ mmol}\)
であることが滴定曲線からすぐに読み取ることができます.\(\rm{NaOH}\)を加えると\(\rm{CH_3COONa}\)が生成され,\(\rm{CH_3COONa\ →\ CH_3COO^-\ +\ Na^+}\)と\(\rm{CH_3COO^-}\)が生成されるのでしたね!
そしてこの値を\(K_{\rm{a}}\)にそのまま代入していきましょう.
\(K_{\rm{a}} = \large \frac{4.0}{2.0} \small \rm{[H^+]} = 2[H^+]\)
\({\rm{[H^+]}} = \large \frac{1}{2} \small K_{\rm{a}} = 1.0 × 10^{-5}\ \rm{mol/L}\)
よって,\(\rm{pH}\)はすぐに\(5\)と求めることができます.
このように滴定曲線をかくと,驚異的な速さで\(\rm{pH}\)を求められるようになります!練習して必ず使いこなせるようになってくださいね!



コメント