【京大過去問解説】京大化学2018 大問1解説|難しい問題ほどグラフを書いて考えよう！

KUT

今回は\(2018\)年京都大学の大問\(1\)について解説していきます．今回は，

単位変換の早技
グラフを書いて状況を可視化する

を特にポイントとしています．昨日の自分より少しでもレベルアップしていきましょう！

大問1の総評
大問\(1\)
1. (\(\rm{a}\))：氷の結晶
2. (\(\rm{b}\))：\(\rm{NaCl}\)水溶液の電気分解・緩衝液
  1. 問\(\rm{4：NaOH}\)の工業的プロセス
    1. \((\rm{\hspace{.18em}i\hspace{.18em}})\)：電極でのイオン反応式
    2. \((\rm{i\hspace{-.01em}i})\)：陽イオン交換膜の除去
  2. 問5：\(\rm{NaHCO_3}\)-\(\rm{Na_2CO_3}\)緩衝液
最後に

大問1の総評

こんにちは，\(\rm{KUT}\)です．

本記事では，\(2018\)年京大化学の大問\(1\)について解説していきます．
また解説に加えて，それぞれの問題で覚えておいてほしいポイントについて詳しく説明していきます．

京大の化学は難しいという印象が強い方が多いと思いますが，京大化学には難しい問題と標準問題の\(2\)つがあります．ここで，受験生が対策すべきことが\(2\)つあります．

\(1\)つ目は，標準問題を最後まで解き切る力を身につけることです．これにより，まずは平均点を取ることを目指します．

\(2\)つ目は，難しい問題と標準問題を見分けられる目を養うことです．試験本番は時間制限内に自分の解ける問題を解き切る必要があります．そのため，難しい問題は解かずに，標準問題をしっかりと選択していきながら，最後まで解いていくことが必要になります．

この記事では，問題を選択していく目を養うために，どのようにして判断していくのかということも自分なりに説明していきます．

それでは，\(2018\)年京大化学の大問\(1\)の解説に進んでいきましょう！

大問\(1\)

(\(\rm{a}\))：氷の結晶

氷の結晶に関する問題です．

問題文にある図が見づらいため，解答しにくいですが，京大の入試問題特有の文章の中からヒントを探して解ける問題を解く！という姿勢が大切です．それでは\(1\)問ずつ丁寧に解説していきます．

問1

ア・イ：格子内原子数

正直に言って，問題文に与えられた図から格子内原子数を考えることは難しいです．この図は見にくすぎます…

ただ，問題文に「酸素原子は結晶面中に\(16\)個，結晶格子内に\(4\)個ある」という記述があります．これからなんとか酸素原子の格子内原子数を求めることができます．結晶面中にある場合は，\(\large \frac{1}{2}\)となるので，

酸素原子：\(\large \frac{1}{2} \small × 16 + 4 = 12\) コ

水素原子についても同様に考えることができます．「水素原子は結晶面中に\(16\)個，結晶格子内に\(16\)個ある」ので，

水素原子：\(\large \frac{1}{2} \small × 16 + 16 = 24\) コ

ウ：格子体積

格子体積を求める問題ですが，底面積がひし形です．このひし形は正三角形が\(2\)コくっついているものとわかります．

ここでみなさんは正三角形の面積をすぐに答えられますか？

正三角形は化学などでよく出てくるので，暗記してもらいたいです．正三角形の\(1\)辺の長さを\(a\)とすると，
正三角形の面積 = \(\large \frac{\sqrt{3}}{4} \small a^2\)

入試問題は覚えるところは覚え，考えるところは考えるというメリハリをつけていきましょう．

すると，求める体積\(V\)は，
\(V = \large \frac{\sqrt{3}}{4} \small × 0.780 × 0.780 × 0.740 = \large \frac{1.73}{4} \small × 0.450 = 0.3892\ \rm{nm^3}\)

ここの計算の途中では，問題文で与えられている数値を使っています．
\(0.780 × 0.780 ×0.740 = 0.450\)

最後に単位換算して答えとなります．
\(\rm{1\ nm= 10^{-7}\ cm}\)なので，
\(\rm{0.3892\ nm^3 = 0.3892\ (× 10^{-7}cm)^3 = 0.39 × 10^{-21}\ cm^3}\)

【単位変換】
単位変換は，やり方を覚えておけば一発で仕留めることができます！
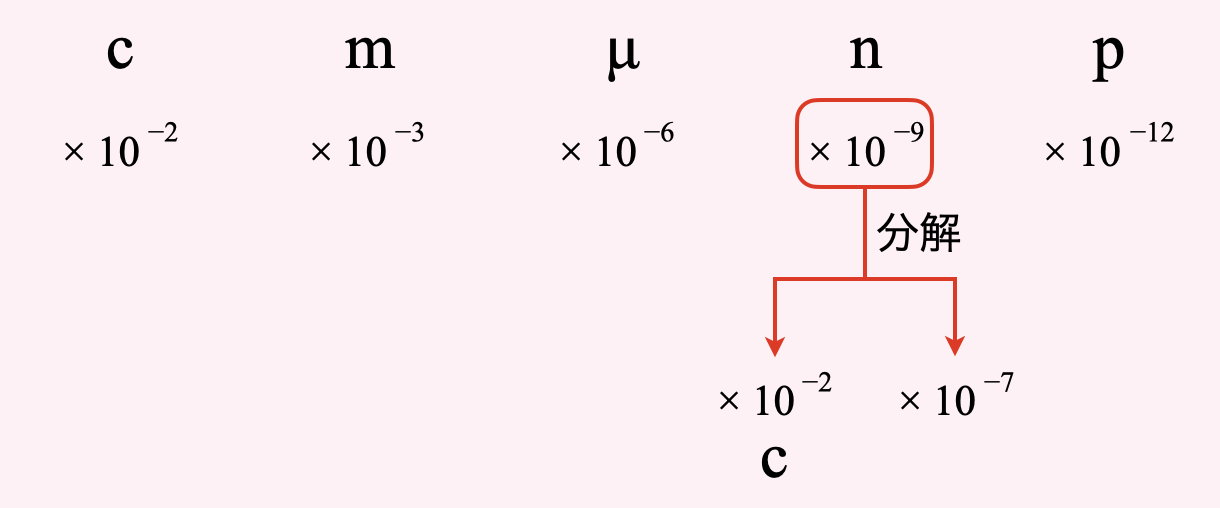
覚えておいてほしい単位は，「\(\rm{c}\)（センチ）」「\(\rm{m}\)（ミリ）」「\(\rm{\mu}\)（マイクロ）」「\(\rm{n}\)（ナノ）」「\(\rm{p}\)（ピコ）」の\(5\)つです．これらの単位は名前を覚えるのが重要ではなく，値を覚える必要があります．それぞれ下のような関係になっています．

このフォーマットを使うと，先程の単位換算も簡単に行うことができます．
今の単位のところに印をつけ（今回の場合は\(\rm{n}\)），そこから求めたい単位（\(\rm{c}\)）とそれ以外に分けます．\(\rm{c}\)は\(10^{-2}\)なので，残りは\(10^{-7}\)となって非常に簡単に分解できます．

エ：結晶密度

結晶密度を計算していきます．密度の計算にはポイントがあります．

【密度計算のポイント】
\(\rm{Step1：}\)質量（\(\rm{g}\)）を計算
\(\rm{Step2：}\)体積（\(\rm{cm^3}\)）を計算
\(\rm{Step3：Step1}\)と\(\rm{Step2}\)を合体！

\(\rm{Step1}\)
質量を数えるときに，ワザの\(1\)つとして「コ」という自分だけの単位を使いましょう．解答では使ってはいけませんが，自分で考えるときには非常にわかりやすくなります．\(\rm{H_2O}\)の分子量は\(18.0\)で，ア・イから格子内には\(12\)コの\(\rm{H_2O}\)があるため，

\(18.0 × 12\ \rm{g\ コ/mol}\)

となります．ここで，アボガドロ定数\(N_{\rm{A}}\)は\(N_{\rm{A}} = 6.0 × 10^{23}\ \rm{コ/mol}\)なので，

\(\rm{\large \frac{18.0\ ×\ 12\ g\ コ/mol}{6.0\ ×\ 10^{23}\ コ/mol} \small = 36 × 10^{-23}\ g}\)

と質量を求めることができました．

\(\rm{Step2}\)
体積はウから\(\rm{0.389 × 10^{-21}\ cm^3}\)であるとわかっています．

\(\rm{Step3}\)
\(\rm{Step1}\)と\(\rm{Step2}\)を合体させて，結晶密度（\(\rm{g/cm^3}\)）を求めていきます．

結晶密度：\(\rm{\large \frac{36\ ×\ 10^{-23}\ g}{0.389\ ×\ 10^{-21}\ cm^3} \small = 0.925\ g/cm^3 = 0.93\ g/cm^3}\)

オ：ファンデルワールス半径

ファンデルワールス半径を求めていきます．

まず，共有結合半径・ファンデルワールス半径のそれぞれを復習していきましょう．参考書に書かれている通りに書くと，

共有結合半径→同種の二原子が共有結合するときの核間距離の半分
ファンデルワールス半径→分子が隣の分子と接触するときの核間距離の半分

となりますが，これではわかりにくいと思います．

つまり，分子内で考えるときが共有結合半径，分子間（分子同士）で考えるときがファンデルワールス半径というわけです．これを図にすると下のようになります．

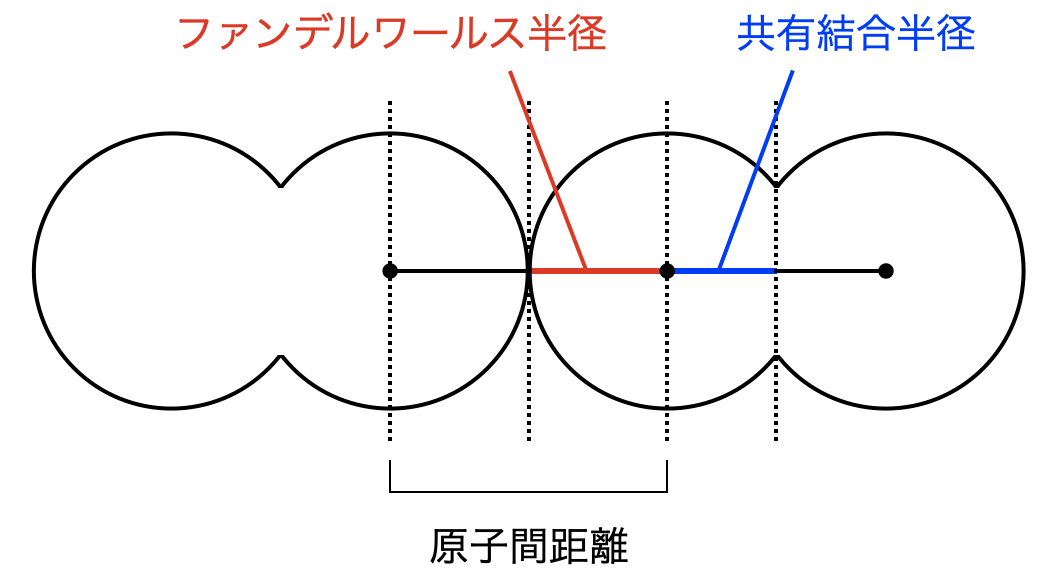
このようにわかりにくい用語は図にしてまとめて覚えてしまいましょう！

今回の問題では，酸素原子のファンデルワールス半径が\(\rm{0.152\ nm}\)なので，酸素原子間の距離は，

\(\rm{0.152 × 2 = 0.304\ nm = 0.30\ nm}\)

実際には氷の結晶での酸素原子間の距離は，\(\rm{0.276\ nm}\)となっています．つまり，ファンデルワールス半径から求めた酸素原子間距離よりも短いというわけです．

この理由として氷は水素結合が生じているからであると考えられます．この水素結合が問\(2\)や問\(3\)に繋がってきます．

問2：氷の水素結合

氷の水素結合に関する問題です．氷は図のような正四面体構造をしています．

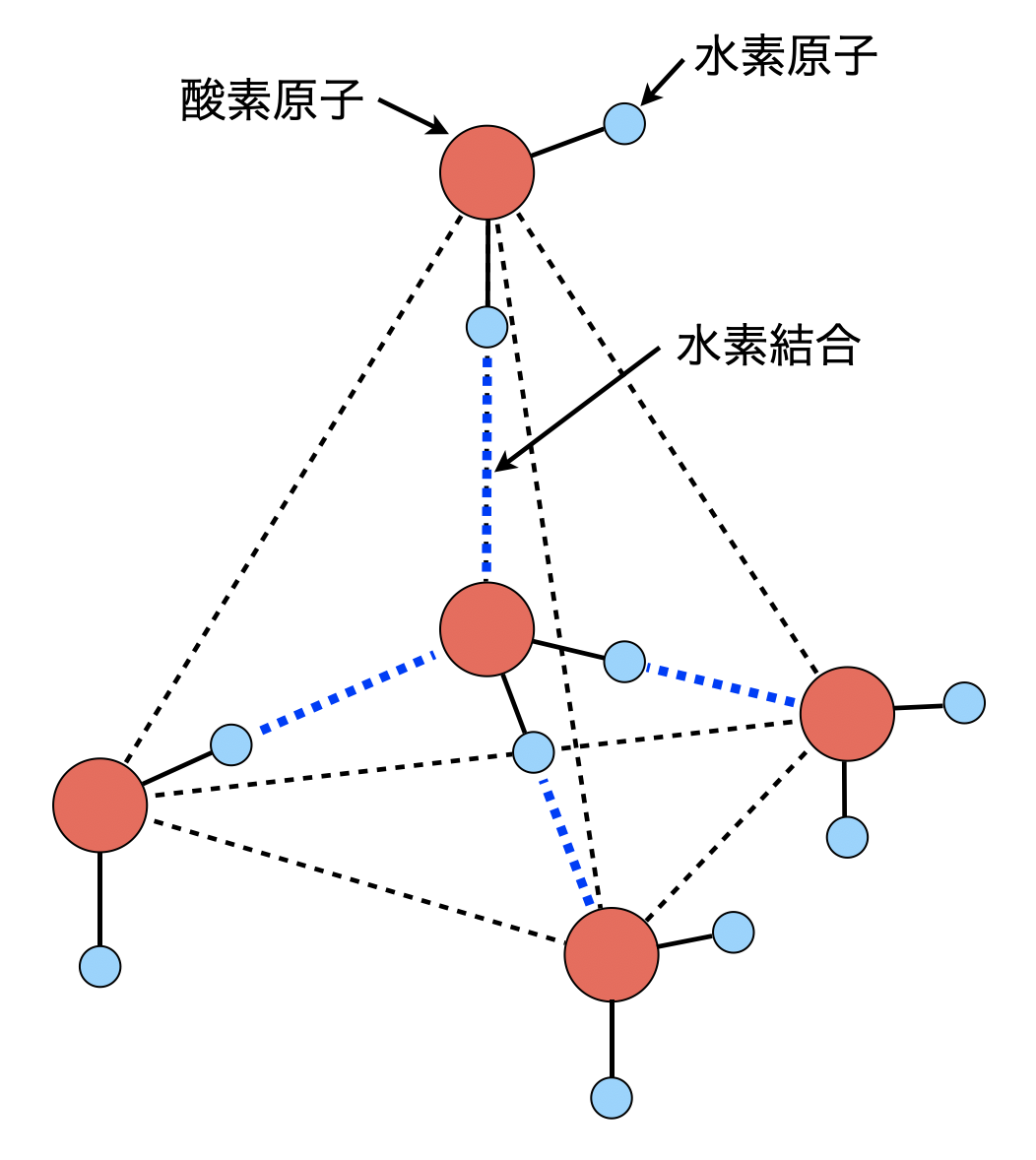
酸素原子の周りの\(4\)方向に水素結合を形成していることがわかります．

氷の水素結合については，以下の記事で覚えておいていただきたい内容を簡潔にまとめていますので，ぜひご覧ください．すぐに読むことができます！

【読むだけでわかる！点数が上がる！】水・氷の2大性質を解説してみた！

氷の結晶に関する記述問題は，入試では頻出です．しかし氷や水の性質に関して問われることは決まっています．今日は水や氷の2大性質を解説しながら，重要ポイントをしっかりと理解し，周りと差を広げていきましょう！

問3：水素結合の結合エネルギー

氷の昇華熱から水素結合\(1\)ヶ所あたりの結合エネルギーを求める問題です．

この問題のポイントは，単位です．下にこの問題をまとめました．

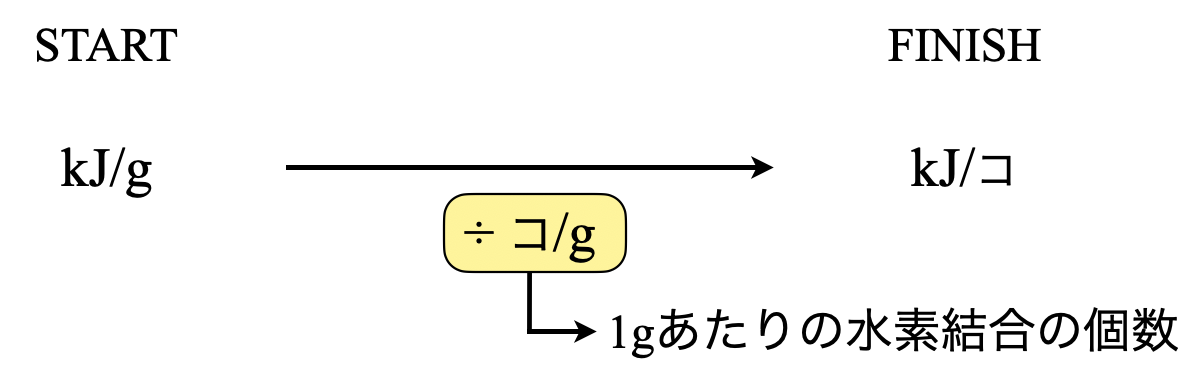
スタートが\(\rm{kJ/g}\)でゴールが\(\rm{kJ/}\)コなので，\(\rm{g/}\)コをかければ良いことになります．

ここでわかりやすくするために，コ\(\rm{/g}\)を考えます．これは，\(\rm{1\ g}\)あたりに水素結合が何ヶ所あるか？という意味になります．

問\(2\)で紹介した記事で詳細を解説しているのですが，水分子\(1\)つあたりに水素結合は\(2\)コあります．つまり，水分子：水素結合 \(= 1：2\)の関係にあります．よって，水のモル質量が\(\rm{18.0\ g/mol}\)，アボガドロ定数が\(6.0 × 10^{23}\ \)コ\(\rm{/mol}\)なので，\(\rm{1\ g}\)あたりの水素結合の個数は以下のようになります．

\(\rm{\large \frac{6.0\ ×\ 10^{23}\ コ/mol}{18.0\ g/mol} \small × 2 = \large \frac{2}{3} \small × 10^{23}\ コ/g}\)

ここで，\(\rm{\large \frac{6.0\ ×\ 10^{23}\ コ/mol}{18.0\ g/mol}}\)は水分子\(\rm{1\ g}\)に水分子が何コ含まれているかということです．ポイントはコが出てきたときには，アボガドロ定数（コ\(\rm{/mol}\)）を使うということです！慣れていきましょう！

最初に示した単位を見て，\(\rm{kJ/}\)コを求めれば\(\rm{OK}\)です！

\(\rm{\large \frac{2.83\ kJ/g}{\large \frac{2}{3}\ ×\ 10^{23}\ コ/g} \small = 4.245 × 10^{-23}\ kJ/コ}\)

最後は単位換算です．
\(\rm{kJ→J}\)にするので，\(\rm{k}\)（キロ）を数字（\(10^3\)）に直します！

\(\rm{4.245 × 10^{-23}\ kJ/コ = 4.245 × 10^{-23} × 10^3\ J/コ = 4.245 × 10^{-20}\ J/コ = 4.2 × 10^{-20}\ J/コ}\)

(\(\rm{b}\))：\(\rm{NaCl}\)水溶液の電気分解・緩衝液

（\(\rm{b}\)）の前半は，\(\rm{NaCl}\)水溶液の電気分解に関する問題で，後半は\(\rm{Na_2CO_3+NaHCO_3}\)の緩衝液に関する問題です．後半が少し難易度が高いので，丁寧に解説していきますね！

問\(\rm{4：NaOH}\)の工業的プロセス

\((\rm{\hspace{.18em}i\hspace{.18em}})\)：電極でのイオン反応式

工業的には，\(\rm{NaOH}\)は\(\rm{NaCl}\)を電気分解することで得られます．

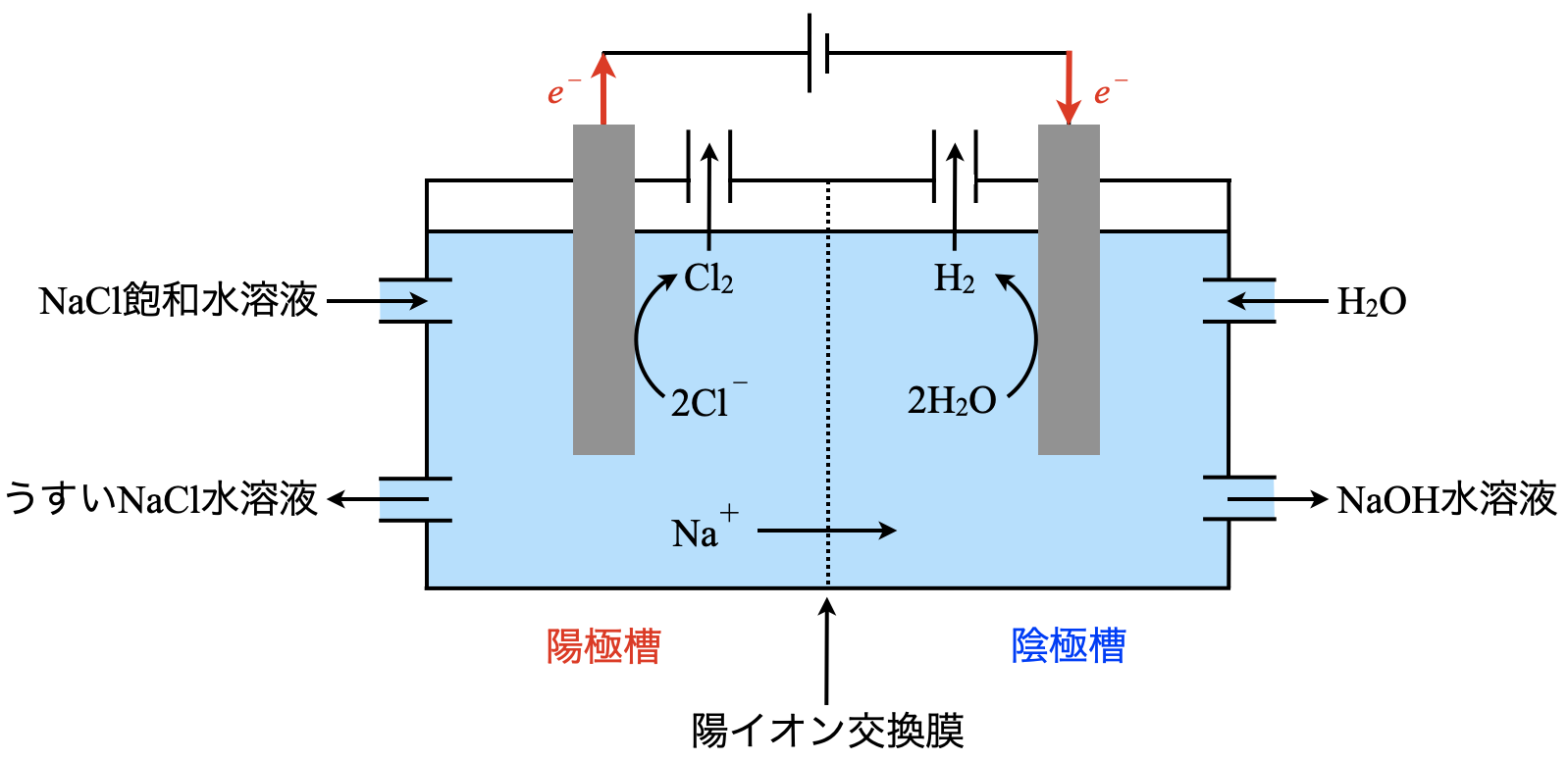
陽極槽には，\(\rm{Na^+}\)と\(\rm{Cl^-}\)があります．この中で\(e^-\)を放出するのは，\(\rm{Cl^-}\)になります．

陽極：\(\rm{2Cl^-\ →\ Cl_2\ +\ }\)\(2e^-\)

陰極槽には，\(\rm{Na^+}\)と\(\rm{OH^-}\)，\(\rm{H_2O}\)があります．この中で\(e^-\)を受け取れるのは，\(\rm{Na^+\ or\ H_2O}\)です．ただ，\(\rm{Na^+}\)はイオン化傾向が大きいので，イオンの状態でいたがります．よって，\(\rm{H_2O}\)が\(e^-\)を受け取ります．

陰極：\(\rm{2H_2O\ +\ }\)\(2e^-\ →\ \rm{H_2\ +\ OH^-}\)

ここで陽イオン交換膜による効果を見ておきます．陰極槽では\(\rm{OH^-}\)が生成されるので，電気的なつりあいが崩れてしまいます．そのため，陽イオン交換膜を通して\(\rm{Na^+}\)が陽極槽→陰極槽に移動し，電気的なつりあいを保ちます．

\(\rm{Na}\)系列についてはこちらの記事で詳しく解説しています．不安な部分がある方はこの機会にしっかりと復習しておきましょう！

【無機化学の完全版】Na系列を総まとめ！|NaClの電気分解や融解塩電解を今日で完璧にしよう！

Naには多くの性質があるのですが，整理して覚えられていますか？今回のポイントは，Na系列の全体像とその性質，Naの融解塩電解NaClの電気分解です．これら以外の性質についても詳しく解説していくので，少しでも自分のものにしてくださいね！

\((\rm{i\hspace{-.01em}i})\)：陽イオン交換膜の除去

電気分解の途中で，液の供給と排出を止め，陽イオン交換膜を除去すると，電解液は\(\rm{NaCl\ +\ NaOH\ +\ H_2O}\)の混合溶液となります．溶液内には，\(\rm{Na^+}\)，\(\rm{Cl^-}\)，\(\rm{OH^-}\)，\(\rm{H_2O}\)が存在します．

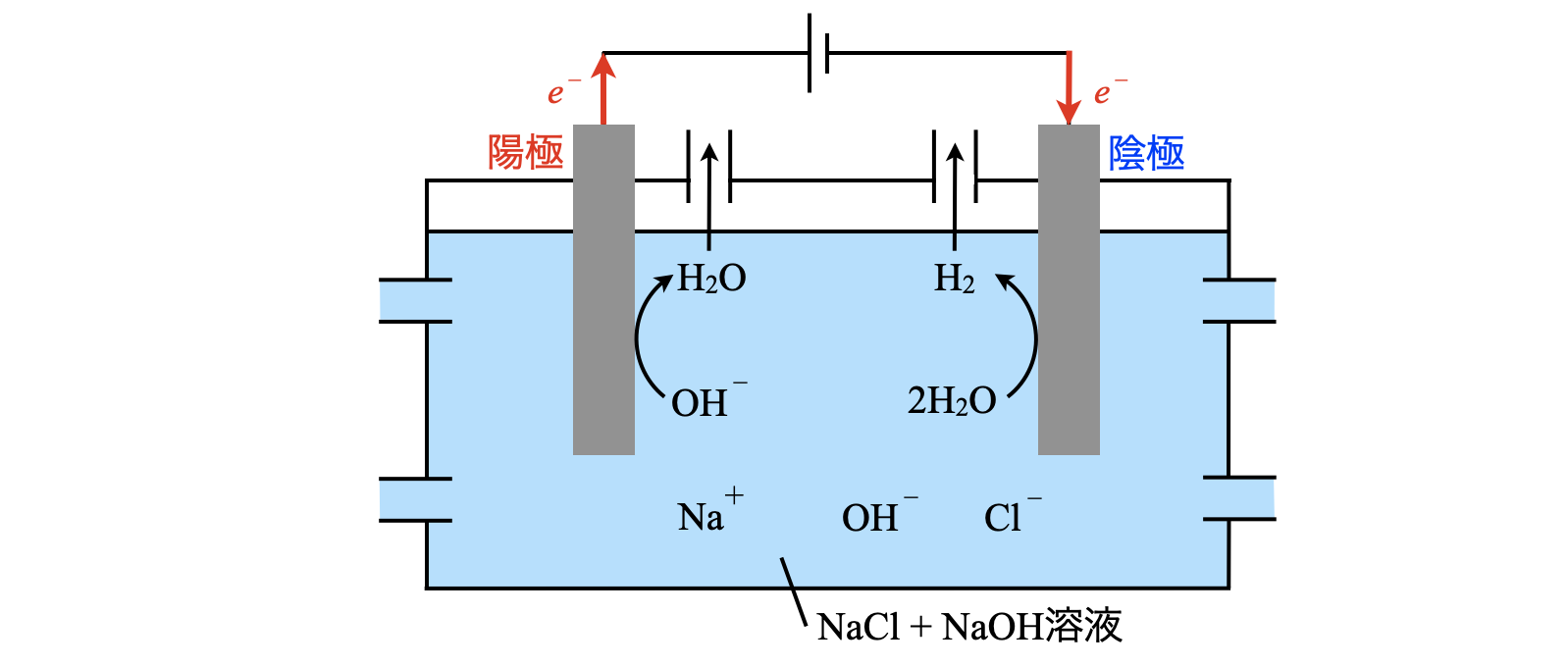
陽極で\(e^-\)を放出できるのは，\(\rm{Cl^-}\)と\(\rm{OH^-}\)があります．ここで問題文に新たな反応が起こったとあるので，\(\rm{OH^-}\)が反応したとわかります．

陽極：\(\rm{4OH^-\ →\ O_2\ +\ }\)\(4e^-\ +\ \rm{2H_2O}\)

陰極で\(e^-\)を得られるのは，\(\rm{Na^+}\)と\(\rm{H_2O}\)があります．先ほどと同じ理由で\(\rm{H_2O}\)が\(e^-\)を得ることになります．

陰極：\(\rm{2H_2O\ +\ }\)\(2e^-\ →\ \rm{H_2\ +\ OH^-}\)

問5：\(\rm{NaHCO_3}\)-\(\rm{Na_2CO_3}\)緩衝液

本問は\(\rm{NaHCO_3}\)-\(\rm{Na_2CO_3}\)の緩衝液に関する問題です．この問題では\(\rm{HCO_3^-}\)と\(\rm{CO_3^{2-}}\)の電離平衡のみを考慮し，その電離定数を\(K\)とすると，

\(\rm{HCO_3^-\ ⇄\ CO_3^{2-}\ +\ H^+}\)

\(K = \large \rm{\frac{[CO_3^{2-}][H^+]}{[HCO_3^-]}}\)

この問題のポイントは，\(3\)つです．

①グラフで問題の状況を可視化する
②電離定数\(K\)をモルに変形させる
③\(\rm{pH=10}\)と\(9.9\)で電離定数\(K\)は変化しない

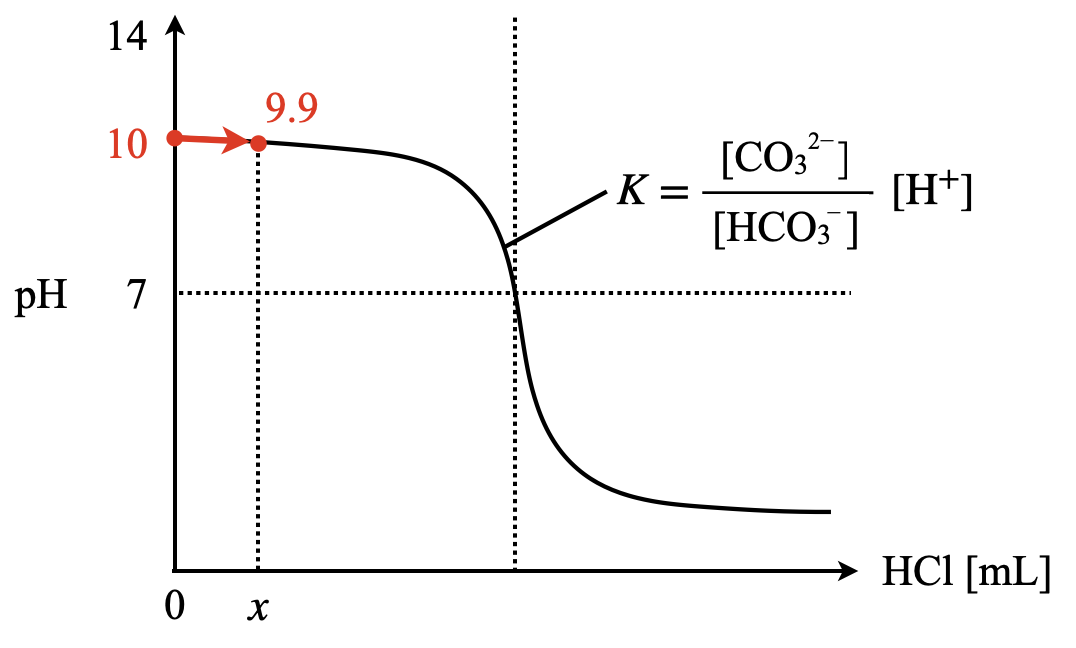
ポイント①
まずグラフを書きながら，問題の状況を整理していきましょう．\(\rm{HCl}\)を\(x\ \rm{[mL]}\)加えたとき，\(\rm{pH}\)が\(9.9\)になったとします．

ポイント②
電離定数\(K\)は一般的に濃度（\(\rm{mol/L}\)）で考えるのですが，この場合体積も考える必要があるため少し面倒です．そのため，以下のように電離定数を変形してしまいましょう．

\(K = \large \rm{\frac{[CO_3^{2-}][H^+]}{[HCO_3^-]}} \small = \)\(\large \frac{n_{\rm{CO_3^{2-}}}}{n_{\rm{HCO_3^-}}} \small \rm{[H^+]}\)

ここで\(n_{\rm{A}}\)は\(\rm{A}\)の物質量（\(\rm{mol}\)）を表しています．

次に，\(\rm{CO_3^{2-}}\)，\(\rm{HCO_3^-}\)の物質量を求めていきます．\(\rm{HCl}\)を\(x\ \rm{[mL]}\)加えたとき，\(\rm{1.00\ mol/L}\)なので，\(x\ \rm{[mmol]}\)加えたことになります．ここで，\(\rm{H^+}\)を加えると，\(\rm{CO_3^{2-}\ +\ H^+\ →\ HCO_3^-}\)の反応が起こります．そのため，

\(\rm{CO_3^{2-}：}\)\(100\ – x\ \rm{mmol}\)，\(\rm{HCl_3^-：}\)\(200 + x\ \rm{mmol}\)

となります．

ポイント③
次に，\(\rm{pH=10}\)と\(9.9\)で電離定数\(K\)は変化しないため，ここで等式を作りましょう！

\(K = \large \frac{100}{200} \small × 10^{-10} = \large \frac{100\ -\ x}{200\ +\ x} \small × 10^{-9.9}\)

\(\large \frac{1}{2} \small × 10^{0.1} = \large \frac{100\ -\ x}{200\ +\ x}\)

問題文から\(10^{0.1} = 1.26\)なのでこれを代入して計算すると，\(x = 14.7\ \rm{mmol}\)であるとわかります．

\(\rm{HCl}\)の濃度は\(\rm{1.00\ mol/L}\)なので，\(\rm{14.7\ mL}\)となります．