【京大過去問解説|秘密のワザを伝授】京大化学2018 大問2解説

KUT

今回は\(2018\)年京都大学の大問\(2\)について解説していきます．今回は，

凝固点降下の溶質計算のコツ
固体を加熱するときの温度変化（凝固点降下の逆向き）
\(\Delta\)を使った方程式を一瞬で書く方法

を特にポイントとしています．昨日の自分より少しでもレベルアップしていきましょう！

大問\(2\)の総評
大問\(2\)
1. (\(\rm{a}\))：凝固点降下
2. (\(\rm{b}\))：気体反応の平衡問題
最後に

大問\(2\)の総評

こんにちは，\(\rm{KUT}\)です．

本記事では，\(2018\)年京大化学の大問\(2\)について解説していきます．
また解説に加えて，それぞれの問題で覚えておいてほしいポイントについて詳しく説明していきます．

京大の化学は難しいという印象が強い方が多いと思いますが，京大化学には難しい問題と標準問題の\(2\)つがあります．ここで，受験生が対策すべきことが\(2\)つあります．

\(1\)つ目は，標準問題を最後まで解き切る力を身につけることです．これにより，まずは平均点を取ることを目指します．

\(2\)つ目は，難しい問題と標準問題を見分けられる目を養うことです．試験本番は時間制限内に自分の解ける問題を解き切る必要があります．そのため，難しい問題は解かずに，標準問題をしっかりと選択していきながら，最後まで解いていくことが必要になります．

この記事では，問題を選択していく目を養うために，どのようにして判断していくのかということも自分なりに説明していきます．

それでは，\(2018\)年京大化学の大問\(2\)の解説に進んでいきましょう！

大問\(2\)

(\(\rm{a}\))：凝固点降下

(\(\rm{a}\))は，凝固点降下について文字式で解答していく問題です．単位が書かれていないのが不親切なので，しっかりと単位を覚えておく必要があります．

問\(1\)：凝固点降下度

凝固点降下に関する問題です．

凝固点降下に関する基礎知識については，こちらの記事をどうぞ！

模試やテストに頻出の凝固点降下・浸透圧を完全マスターしよう！！（厳選練習問題つき！）

今回は溶液の4大特徴である蒸気圧降下・沸点上昇・凝固点降下・浸透圧のうち後半の凝固点降下・浸透圧について解説していきます．この分野テストで頻出なので，しっかりと理解を深めていきましょう！それでは今日も頑張っていきましょう！

今回の問題の条件を図にして見ましょう．

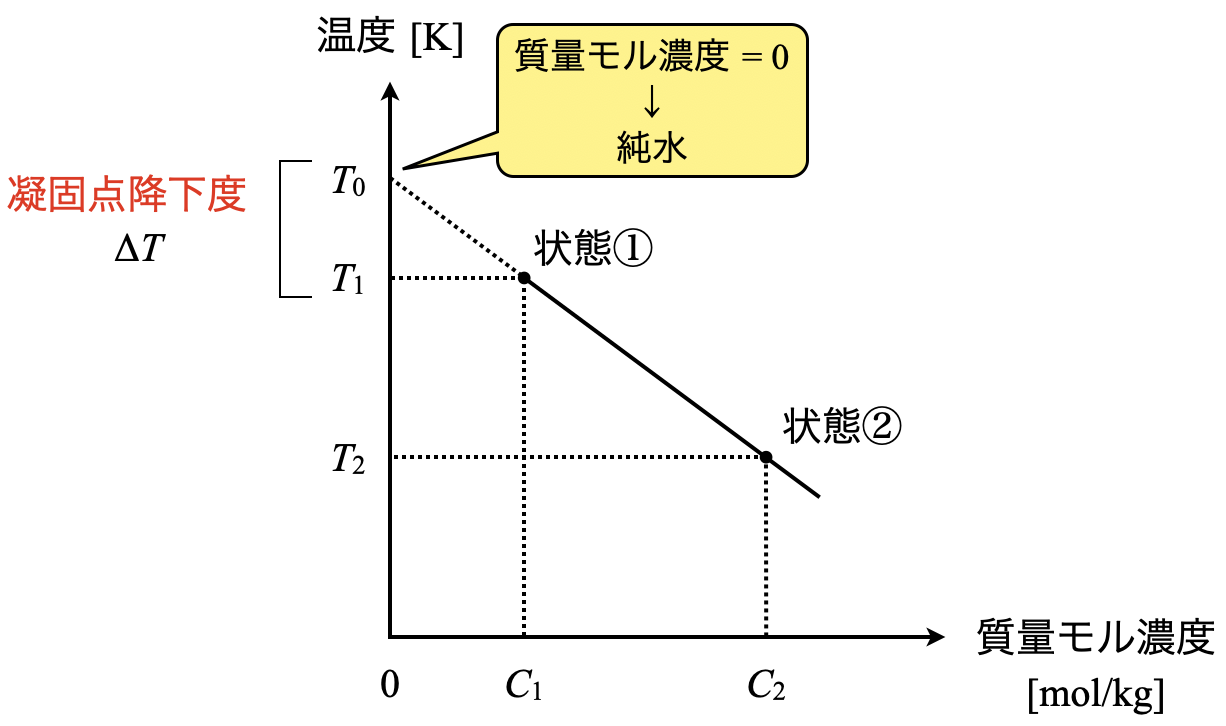
これを\(\Delta T = K_{\rm{f}} C\)に代入していきましょう．

\(T_0\ – T_1 = K_{\rm{f}} C_1\)

\(T_1 = T_0\ – K_{\rm{f}} C_1\)

問2：質量モル濃度

ア：状態②における溶質の質量

まずこの問題を解き始める前に，質量モル濃度や質量パーセント濃度を解く際のワザについて解説していきます．基礎的な内容に自信がない方はぜひこちらの記事を読んでからこの先を読み進めてください！

3つの濃度の使い分けってできてる？3ステップで解説してみた！

みなさんは濃度3種類の公式をすぐに思い出すことができますか？今回は濃度についてどのように覚え，攻略していけばいいのかを詳しく解説していきます．それでは今日も頑張っていきましょう！

私が問題を解く際には，溶媒と溶質を分けた図を書くことを習慣化しています．この図によって混乱を防ぐことができますよ！問題を読みながら，何も考えずに図を書くようになってしまっています．笑　みなさんもこんな感じになってくださいね！

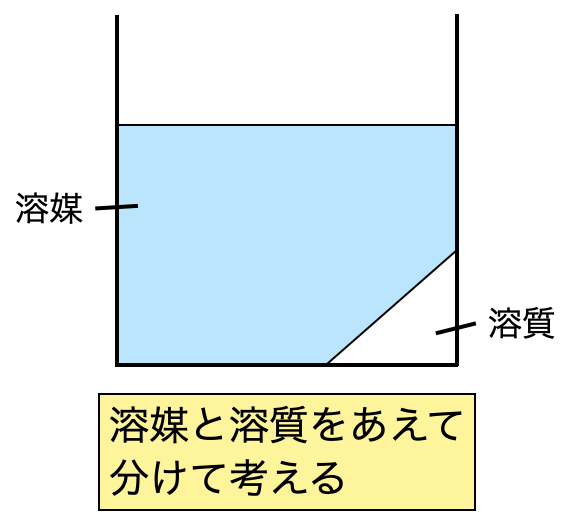
今回の問題では氷が共存しているので，氷も加えた図を書いていきます．そして問題にある溶液の質量\(w_1\)は，氷を含まない質量であることに注意しておいてくださいね！

では実際に解いていきましょう．
まず状態①について，質量モル濃度が\(C_1\ \rm{[mol/kg]}\)，溶質の分子量が\(M_{\rm{s}}\)なので，溶媒\(1\ \rm{kg}\)に溶解している溶質は\(C_1M_{\rm{s}}\ \rm{[g]}\)となります．するとこのときの質量パーセント濃度は，溶質/全体なので以下のようになります．

質量パーセント濃度：\(\large \frac{C_1M_{\rm{s}}}{1000\ +\ C_1M_{\rm{s}}}\)

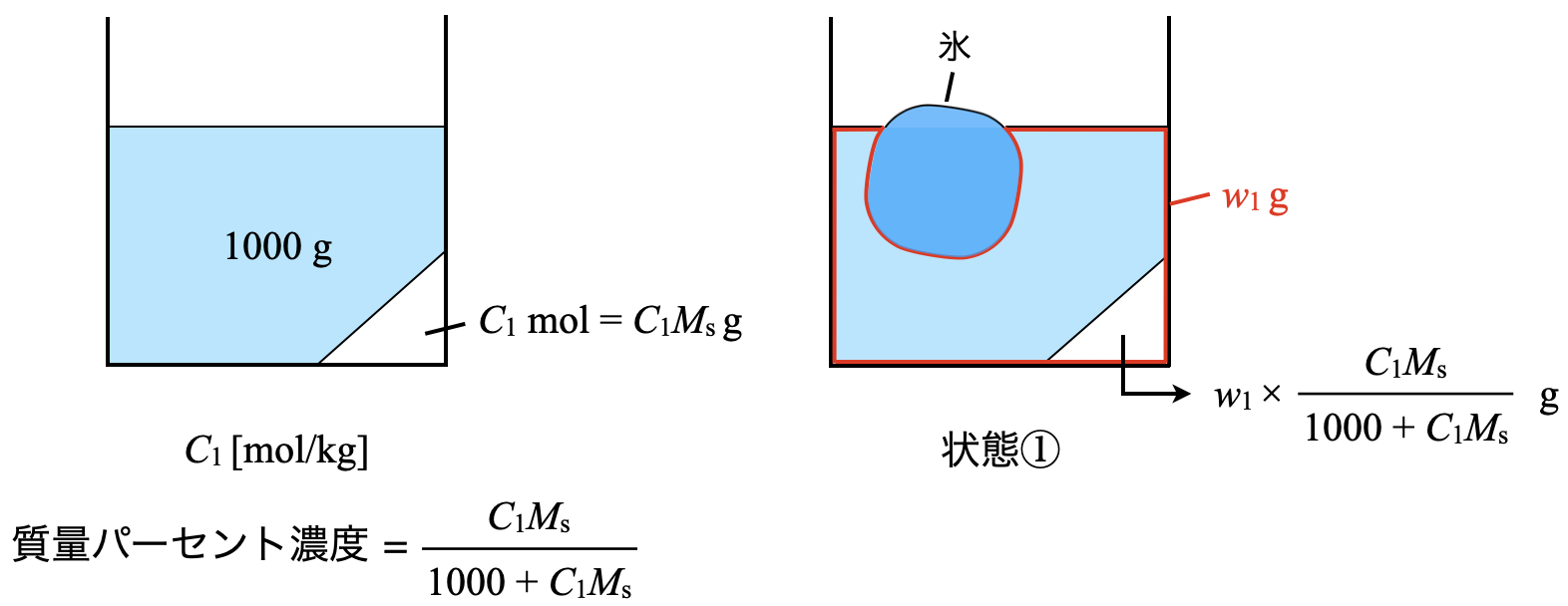
そして状態①の場合，溶液の質量が\(w_1\ \rm{[g]}\)なので，\(w_1\ \rm{[g]}\)のうちの質量パーセント濃度分が溶質であるということです．そのため溶質の質量は以下のようになります．

状態①における溶質の質量：\(w_1 × \large \frac{C_1M_{\rm{s}}}{1000\ +\ C_1M_{\rm{s}}}\ \small \rm{[g]}\)

状態①と状態②では文字の添字が\(1\)と\(2\)の違いしかないので，\(1→2\)に変えるだけで答えとなります．

状態②における溶質の質量：\(w_2 × \large \frac{C_2M_{\rm{s}}}{1000\ +\ C_2M_{\rm{s}}}\ \small \rm{[g]}\)

今回の問題のように問題文の文字に単位がないときは自分で補って考えることで理解しやすくなります．特に，質量モル濃度の単位が\(\rm{mol/kg}\)であることは問題文にも書かれていますが，しっかりと覚えておいてくださいね！

イ：状態②における氷の質量

ここまでくれば後は問題文をしっかりと読んで，立式することで解答することができます．

「溶質の質量は状態①と②で不変」「ビーカー内の物質の総量も状態①と②で不変」からそれぞれ立式していきます．

溶質の質量：\(w_1 × \large \frac{C_1M_{\rm{s}}}{1000\ +\ C_1M_{\rm{s}}} \small = w_2 × \large \frac{C_2M_{\rm{s}}}{1000\ +\ C_2M_{\rm{s}}}\)

物質の総量：\(M_1\ +\ w_1\ =\ M_2\ +\ w_2\)

この\(2\)式から\(w_2\)を消去していきます．物質の総量の式から，\(M_2\ =\ M_1\ +\ w_1\ -\ w_2\)となるので，溶質の質量の式を\(w_2\)について解きます．すると，

\(w_2 = \large \frac{1000\ +\ C_2M_{\rm{s}}}{1000\ +\ C_1M_{\rm{s}}} \small × \large \frac{C_1}{C_2} \small \ w_1\)

よって，

\(M_2 = M_1 + w_1 \left( 1\ – \large \frac{1000\ +\ C_2M_{\rm{s}}}{1000\ +\ C_1M_{\rm{s}}} \small × \large \frac{C_1}{C_2} \right)\)

となります．

問3：固体を加熱するときの温度変化

冷却曲線の①〜②については，先ほど紹介した凝固点降下に関する記事に詳細を書いていますので，そちらをご覧ください．

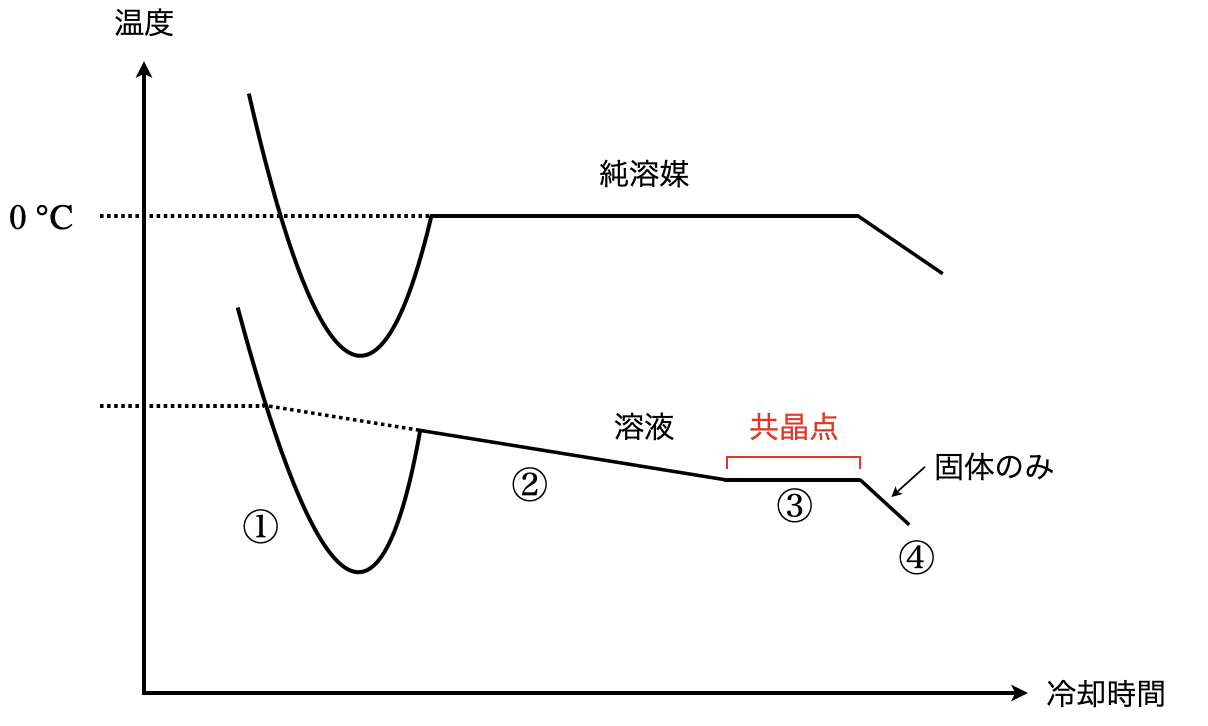
③と④については簡単に説明しておきます！

③からは溶媒と溶質のそれぞれについて見ていく必要があります．
まずは溶媒です．溶媒は凝固が進み，溶液の濃度が一定になります．すると，次は溶質に変化が現れます．溶液に溶けることができなくなった溶質の一部が析出し，溶媒の凝固と溶質の析出が同時に行われるようになります．

これ以降は溶液の濃度（\(C\)）が一定なので，凝固点降下はこれ以上進まず，温度一定（\(\Delta T = 0\)）となります．これは\(\Delta T = K_{\rm{f}} C\)からわかりますね！このときの温度を共晶点といい，固体混合物を共晶といいます．

④では，さらに熱を加えると，すべての溶媒が凝固し，すべての溶質も析出します．この後は冷却により，固体混合物として温度が下がっていきます．

ここまでが冷却曲線の復習となります．

ここから今まで考えてきたものを逆向きに，つまり固体混合物の温度を上昇していきます．
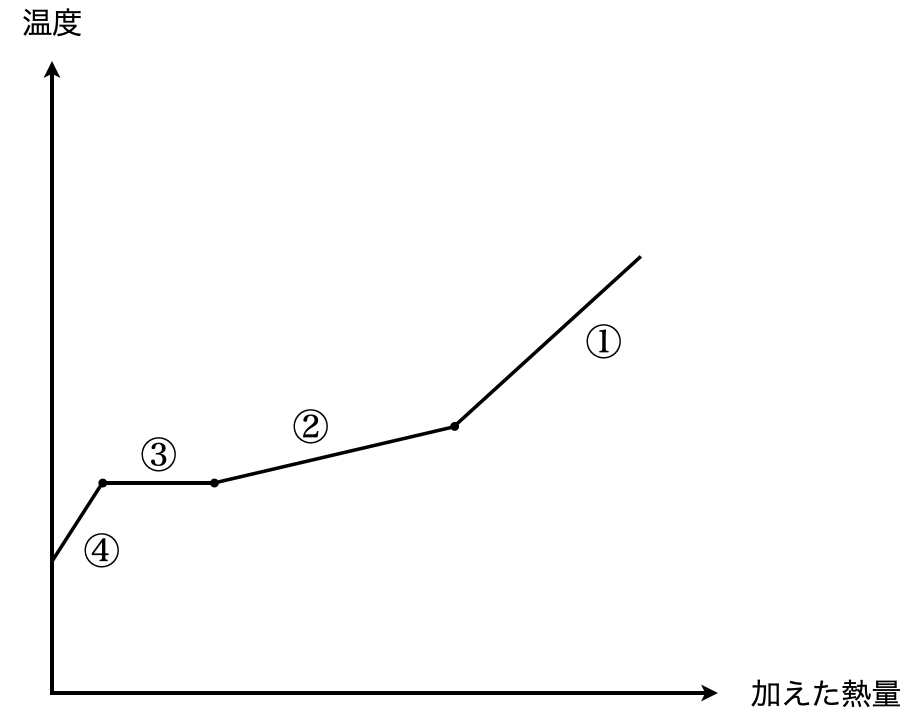
④固体混合物に熱を加えると，直線的に温度が上昇し，氷の融解に加え，溶質も溶解していきます．
③濃度が一定となり，温度一定を保ちながら溶液が増加していきます．
②すべての溶質が溶解後，氷の融解が続き，温度が直線的に上昇していきます．
①すべての氷が溶解すると，あとは一定の割合で温度が上昇していきます．

これをグラフにすると下のようになります．

過冷却は，名前の通り冷却するときにしか現れないため，今回のような温度を上昇させていくときには現れません．注意してくださいね！

(\(\rm{b}\))：気体反応の平衡問題

(\(\rm{b}\))は気体反応の平衡に関する問題です．あ〜うまでは解きやすいですが，えに関しては少し計算が煩雑です．工夫しながら解く方法を解説していきます．

あ：物質量の比

まずは問題の状況を整理していきます．

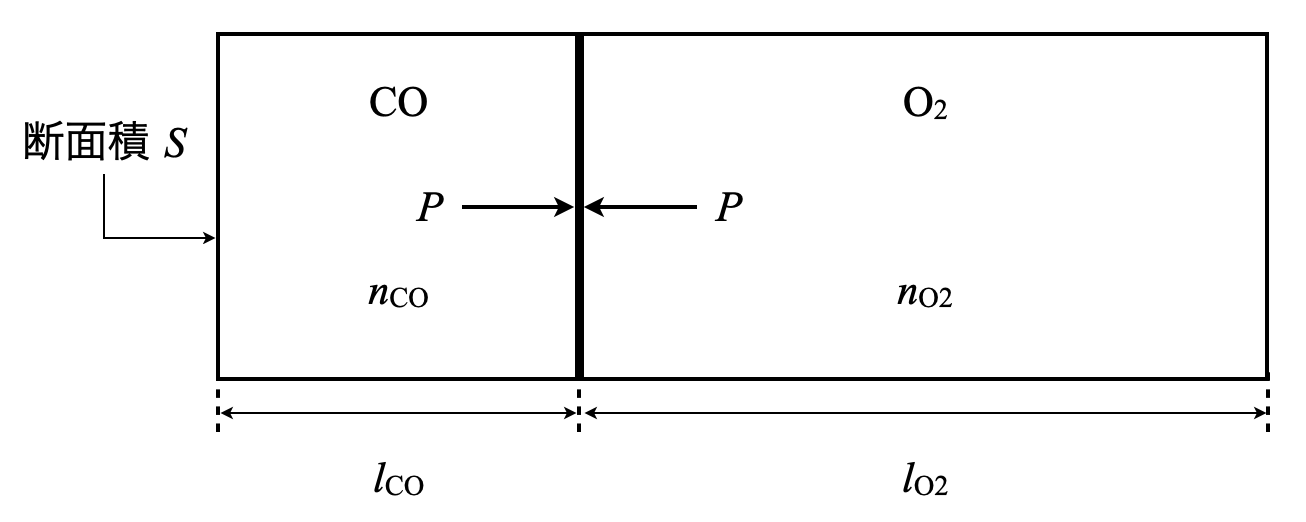
「可動壁が動かない\(=\)左右での圧力が等しい」ということなので，その圧力を\(P\)としています．容器内が気体なため，状態方程式：\(pV = nRT\)を使って\(\rm{OK}\)です！

ここで\(1\)つポイントがあります．左右についてそれぞれ状態方程式を立てて計算してもよいのですが，左右で等しい値に着目することで，もっと早く計算することができます．

今回の場合，\(P\)，\(T\)が等しいので，\(P V = nRT\)から\(V = \large \frac{RT}{P} \small n = kn\)とできます．つまり，\(k = \large \frac{V}{n}\)とでき，\(k\)について\(1\)つの等式にできるというわけです．

\(\large \frac{Sl_{\rm{CO}}}{n_{\rm{CO}}} \small = \large \frac{Sl_{\rm{O_2}}}{n_{\rm{O_2}}}\)

よって，

\(\large \frac{n_{\rm{CO}}}{n_{\rm{O_2}}} \small = \large \frac{l_{\rm{CO}}}{l_{\rm{O_2}}}\)

い：平衡移動

次に，可動壁を取り除いて，平衡になったときのそれぞれの物質量（モル）変化を考えていきます．\(\rm{CO_2}\)が\(a\ \rm{[mol]}\)生成したとすると，以下のようになります．

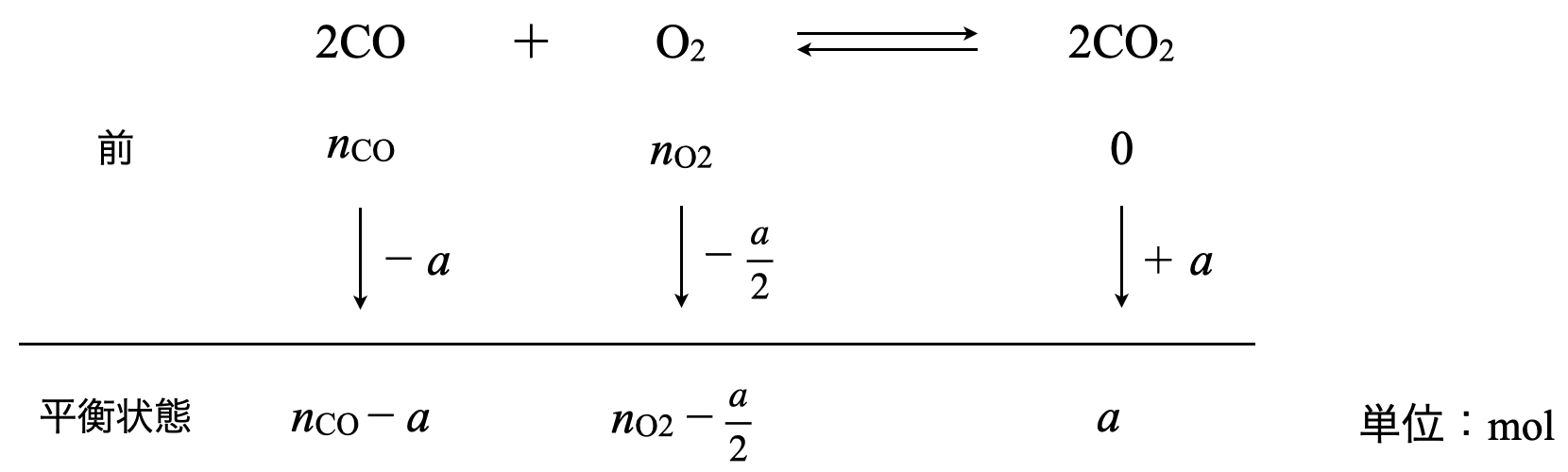
これから平衡後の気体分子の物質量の合計は以下のようになります．

\((n_{\rm{CO}}\ – a) + \left( n_{\rm{O_2}}\ – \large \frac{a}{2} \right) \small \ + a = n_{\rm{CO}}\ + n_{\rm{O_2}}\ – \large \frac{a}{2}\ \small \rm{[mol]}\)

う：平衡移動による圧力変化

この問題も状態方程式を考えることですぐに解くことができます．

\(T\)，\(V\)一定なので， \(p = kn\)となり，\(n\)が変化すれば\(p\)も同じように変化することがわかります．

ここで，最初容器内にあった物質量は，\(n_{\rm{CO}}\ + n_{\rm{O_2}}\ \rm{[mol]}\)であったので，\(\large \frac{a}{2}\ \small \rm{[mol]}\)だけ減少していることがわかります．そのため，圧力\(p\)も減少しています．

え：圧平衡定数\(K_{\rm{p}}\)

最後は圧平衡定数\(K_{\rm{p}}\)を求める問題ですが，\(a\)の代わりに\(x\)を使って求める必要があります．そのため問題文にある\(\large \frac{xRT}{V}\)だけ圧力が減少したという部分を立式していきましょう．

ここで時短テクニックを紹介します．

【\(\Delta\)を使った立式】
変化する変数だけに\(\Delta\)をつけることで簡単に式を作ることができます．

この問題で説明すると，\(T\)，\(V\)一定なので，変化するのは\(p\)，\(n\)ということになります．この\(p\)，\(n\)→\(\Delta p\)，\(\Delta n\)とすると変化を考慮した状態方程式を簡単に作ることができます．

\(\Delta p V = \Delta n RT\)

京大化学などでは頻出の変化なのでしっかりと理解しておいてくださいね！

この式を理解するには，下のような例を考えてみましょう．
平衡前：\(p_1\)，\(V\)，\(n_1\)，\(T\)
平衡後：\(p_2\)，\(V\)，\(n_2\)，\(T\)

この\(2\)つについてそれぞれ状態方程式を作ります．

平衡前：\(p_1 V = n_1 RT\)
平衡後：\(p_2 V = n_2 RT\)

この\(2\)式について（平衡後） \(-\) （平衡前）とすると，

\((p_2\ – p_1) V = (n_2\ – n_1)RT\)

そして\(\Delta\)というのは変化量を表すので，\(\Delta p = p_2\ – p_1\)，\(\Delta n = n_2\ – n_1\)を意味しています．すると，

\(\Delta p V = \Delta n RT\)

を導くことができました．この式変形を理解した上で，すぐに\(\Delta\)を使った式を立式できるように練習していきましょう！

さて，今回の問題について考えると，

\(\Delta P = \large \frac{\Delta nRT}{V} \small = \large \frac{xRT}{V} \small → \Delta n = x\)

\(\Delta n = \large \frac{2}{a}\)

この\(2\)式から\(a\)と\(x\)の関係が分かります．

\(a = 2x\)

すると，平衡後の物質量はそれぞれ\(x\)を用いて以下のようになります．

\({\rm{CO}}：n_{\rm{CO}}\ – 2x\ \rm{[mol]}\)，\({\rm{O_2}}：n_{\rm{O_2}}\ – x\ \rm{[mol]}\)，\({\rm{CO_2}}：2x\ \rm{[mol]}\)

あとは，圧平衡定数\(K_{\rm{p}}\)の式にぼんぼん代入していけば\(\rm{OK}\)です．

\(K_{\rm{p}} = \large \frac{P_{\rm{CO_2}}^2}{P_{\rm{CO}}^2\ P_{\rm{O_2}}} \small = \large \frac{\left( \large \frac{2xRT}{V} \right)^2}{\left( \frac{(n_{\rm{CO}}\ -\ x)RT}{V} \right)^2 \small \cdot \large \frac{(n_{\rm{O_2}}\ -\ x)RT}{V}} \small = \large \frac{4x^2V}{(n_{\rm{CO}}\ -\ 2x)^2 (n_{\rm{O_2}}\ -\ x)RT}\)

最後の計算は煩雑ですが，落ち着いて計算していきましょう．