今回のメニューです!
✅強酸・弱酸の\(\rm{pH}\)計算方法
物質の変化の中の「酸・塩基」について徹底解説していきます。
酸・塩基の中で、\(\rm{pH}\)計算をできるようになるのが一つの大きなポイントになります。
強酸と弱酸の違いなどをわかりやすく解説していくので、ぜひ最後までご覧だくさい!
\(\rm{pH}\):水素イオン指数
水溶液の酸性・塩基性の強さを表現するものに\(\rm{pH}\)というものがあります。
この\(\rm{pH}\)の値を水素イオン指数といいます。
\(\rm{pH}\)は次の式で求めることができます。
\(\rm{pH=- log_{10}[H^+]}\)
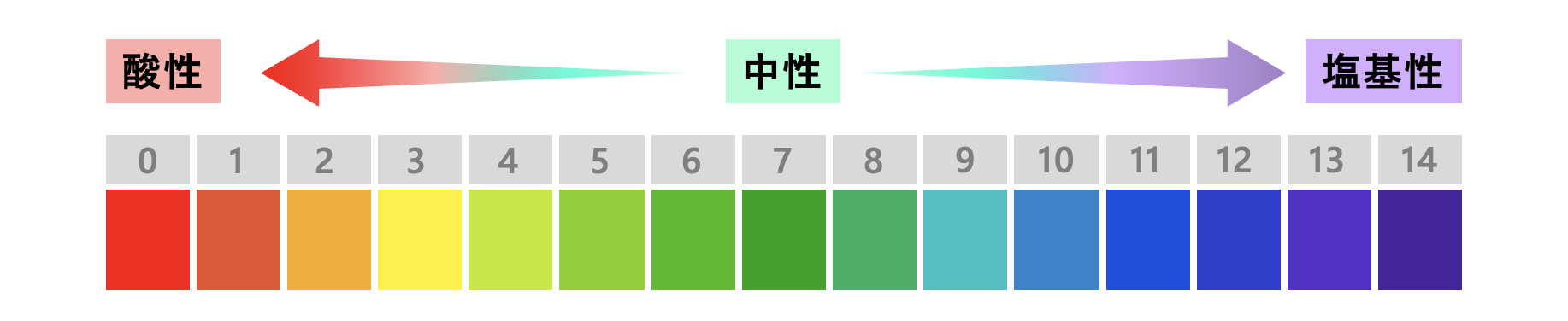
\(\rm{pH}\)は\(\ 0 \sim 14\)で変化します。
以前の記事で解説したように、中性の水溶液は\(\rm{25°C}\)で\(\rm{[H^+]=1.0×10^{-7}\ mol/L}\)なので、
\(\rm{pH=-log_{10}[H^+]=-\log_{10}(1.0×10^{-7})=7}\)となります。
・\(\rm{pH \lt 7}\):酸性の水溶液
・\(\rm{pH \gt 7}\):塩基性の水溶液
なので、酸性が強いほど\(\rm{pH}\)は小さくなり、塩基性が強いほど\(\rm{pH}\)が大きくなります。
そして、\(\rm{pH}\)が\(7\)に近づくほど、酸・塩基ともに弱くなるという風に理解しておきましょう!
\(\rm{pH}\)を用いると、様々な水溶液の性質を表現できるので、化学だけでなく農学や医学の世界でも活用されています。
\(\rm{pOH}\):水酸化物イオン指数
では次に、水酸化物イオンの指数を表す\(\rm{pOH}\)について解説していきます。
\(\rm{pH}\)と同様に考えると、\(\rm{pOH}\)は次の式で求めることができます。
\(\rm{pOH=-log_{10}[OH^-]}\)
\(\rm{pOH}\)は\(\ 0 \sim 14\)で変化します。
では、水のイオン積から\(\rm{pH}\)と\(\rm{pOH}\)の関係を求めてみましょう。
水のイオン積:\(K_w = \rm{[H^+][OH^-]=1.0×10^{-14}}\)
この両辺について\(\rm{-log_{10}}\)をとると、次のようになります。
\(\rm{-log_{10}([H^+][OH^-])=-log_{10}(1.0×10^{-14})}\)
\(\rm{-log_{10}[H^+]-log_{10}[OH^-]=14}\)
ここで、\(\rm{pH=-log_{10}[H^+]、pOH=-log_{10}[OH^-]}\)なので、
\(\rm{pH+pOH=14}\)
となります。
つまり、\(\rm{pH}\)と\(\rm{pOH}\)の和は常に\(14\)になるというわけです。
\(\rm{pH}\)計算
では、\(\rm{pH}\)の求め方がわかったところで、強酸や弱酸の水溶液の\(\rm{pH}\)を求めていきます。
モル濃度\(C\ [\rm{mol/L}]\)の水溶液の\(\rm{pH}\)をまとめると、次のようになります。
これを頭に入れた上で、各水溶液の\(\rm{pH}\)を考えていきましょう。
| 電離度\(\ \alpha\) | \(\rm{[H^+]}\) | ||
| 強酸 | \(1\) | \(C\) | |
| 弱酸 | \(1-\alpha≒1\)と近似できるとき | \(\alpha < 0.05\) | \(\sqrt{CK_a}\) |
| \(1-\alpha≒1\)と近似できないとき | \(\alpha > 0.05\) | \(\sqrt{C\alpha}\) |
強酸の\(\rm{pH}\)計算
強酸の例として、塩酸\(\rm{HCl}\)を考えてみましょう。
モル濃度\(C\ [\rm{mol/L}]\)の塩酸\(\rm{HCl}\)の\(\rm{pH}\)を求めてみます。
強酸である塩酸の電離度はほぼ\(1\)なので、水溶液中ではほぼ完全に\(\rm{H^+}\)と\(\rm{Cl^-}\)に電離します。
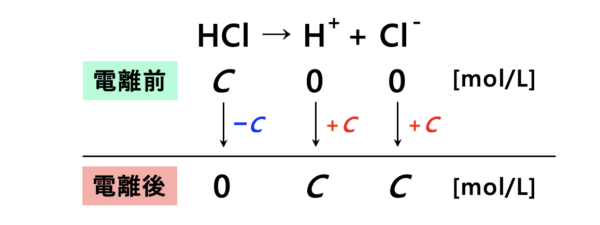
つまり、電離後の\(\rm{[H^+]}\)のモル濃度は\(C\ [\rm{mol/L}]\)なので、強酸の\(\rm{pH}\)は次のようになります。
\({\rm{pH=-log_{10}}}C\)
反応式を書いて電離前後の濃度を考えると、混乱なく理解できると思います。
弱酸の\(\rm{pH}\)計算
では次に、弱酸の\(\rm{pH}\)を求めていきましょう。
弱酸として酢酸\(\rm{CH_3COOH}\)を考えてみます。
弱酸である酢酸は水溶液中で電離度\(\alpha\)しか電離しません。
この電離度とは、水溶液全体中で割合\(\alpha\)しか電離しないという意味でした。
これをふまえてモル濃度\(C\ [\rm{mol/L}]\)の酢酸の\(\rm{pH}\)を求めてみましょう。
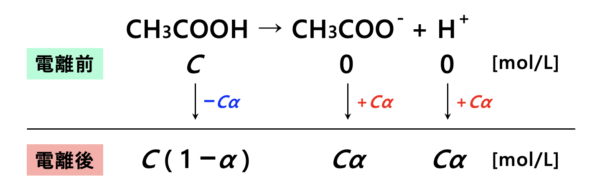
すると、上のように濃度が変化することがわかります。
なので、酸の電離定数\(K_a\)は
\(K_a= \large \frac{[{\rm{CH_3COO^-}}][{\rm{H^+}}]}{[{\rm{CH_3COOH}}]} \small = \large \frac{(C\alpha)^2}{C(1-\alpha)} \small = \large \frac{C\alpha^2}{1-\alpha}\)
となります。
ここで、この電離度\(\alpha\)の大きさによって、場合分けしていきます。
① \(1-\alpha≒1\)と近似できるとき
\(\alpha \lt 0.05\)のとき、電離度\(\alpha\)は\(1\)より十分に小さいので、\(1-\alpha≒1\)と近似することができます。
水素イオン濃度\({\rm{[H^+]}} = C\alpha\)なので、電離度\(\alpha\)を酸の電離定数\(K_a\)で表していきましょう。
\(K_a=C\alpha^2\)なので、電離度\(\alpha\)は\(\alpha=\sqrt{\large \frac{K_a}{C}}\)と表現することができます。
以上から、水素イオン濃度\(\rm{[H^+]}\)は
\({\rm{[H^+]}} = C\alpha=\sqrt{CK_a}\)
と求めることができます。
② \(1-\alpha≒1\)と近似できないとき
では次に、\(1-\alpha≒1\)と近似できない場合を考えてみましょう。
これは電離度\(\alpha\)が\(5\%\)以上というイメージです。
\(K_a=\large \frac{C\alpha^2}{1-\alpha}\)を式変形すると、\(C\alpha^2+K_a\alpha-K_a=0\)となります。
これは\(\alpha\)の二次方程式なので、解の公式を使うと、電離度\(\alpha\)は次のようになります。
(電離度\(\alpha\)は正なので、「\(-\)」は除外しました。)
\(\alpha=\large \frac{-K_a+\sqrt{{K_a}^2+4CK_a}}{2C}\)
これを\({\rm{[H^+]}} = C\alpha\)の\(\alpha\)に代入していきましょう。
\({\rm{[H^+]}} = \large \frac{-K_a+\sqrt{{K_a}^2+4CK_a}}{2}\)
となります。
実践練習
それでは、ここまでの内容を踏まえて、強酸・強塩基、弱酸・弱塩基の\(\rm{pH}\)を実際に求めてみましょう。
問題\(\ 1\):強酸の\(\rm{pH}\)
\(\rm{0.20\ mol/L}\)の塩酸の\(\rm{pH}\)は?
ただし、\(\rm{log_{10}2=0.30}\)とする。
塩酸は強酸なので、電離度は\(1\)になります。
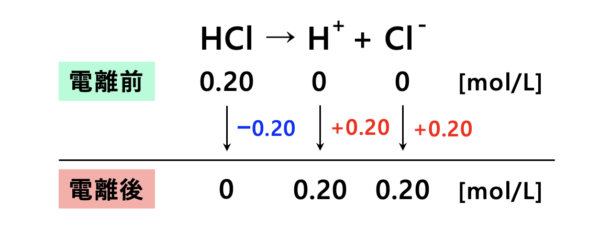
この図から、水素イオン濃度\(\rm{[H^+] = 0.20\ mol/L}\)となります。
なので、
\(\rm{pH=-log_{10}[H^+]=-log_{10}(0.20)=1-\log_{10}2=1-0.3=0.7}\)
答え:\(\rm{pH=0.7}\)
問題\(\ 2\):強塩基の\(\rm{pH}\)
\(\rm{0.010\ mol/L}\)の水酸化ナトリウム水溶液の\(\rm{pH}\)は?
\(\rm{NaOH}\)は強塩基なので、電離度は\(1\)になります。
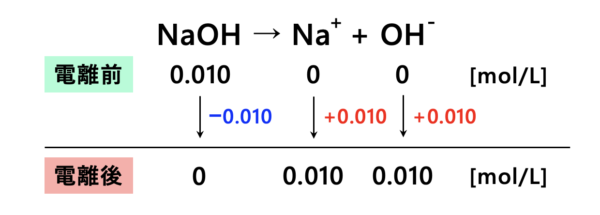
この図から、\(\rm{[OH^-]=0.010\ mol/L}\)となります。
なので、
\(\rm{pOH=-log_{10}[OH^-]=-log_{10}(0.010)=2}\)
\(\rm{pH+pOH=14}\)なので、\(\rm{pH=14-2=12}\)とわかります。
答え:\(\rm{pH=12}\)
問題\(\ 3\):弱酸の\(\rm{pH}\)
\(\rm{0.02\ mol/L}\)の酢酸水溶液の\(\rm{pH}\)は?
ただし、酢酸の電離定数\(K_a\)を\(\rm{1.8×10^{-5}\ mol/L}\)、\(\rm{log_{10}2=0.30}\)、\(\rm{log_{10}3=0.48}\)とする。
酢酸は弱酸なので、\(3\)ステップで解説していきます!
① 電離度\(\alpha\)を電離定数\(K_a\)で表現する
弱酸である酢酸の\(\rm{pH}\)を求めるためには、まず電離度\(\alpha\)を電離定数\(K_a\)で表す必要があります。

上の図から、酢酸の電離定数\(K_a\)は次のようになります。
\(K_a=\large \frac{[{\rm{CH_3COO^-}}][{\rm{H^+}}]}{[{\rm{CH_3COOH}}]} \small = \large \frac{C \alpha^2}{1-\alpha}\)
ここで、電離度\(\alpha\)が\(1\)より十分に小さいと仮定し、\(1-\alpha≒1\)とすると、\(K_a≒C \alpha^2\)となります。
なので、電離度\(\alpha\)は
\(\alpha = \sqrt{\large \frac{K_a}{C}}\)
と表現できます。
②電離度\(\alpha\)を求める
上の式に\(K_a=1.8×10^{-5}\ \rm{mol/L}\)と\(C=0.02\ \rm{mol/L}\)を代入して、電離度\(\alpha\)を求めていきましょう。
\(\alpha = \sqrt{\large \frac{1.8×10^{-5}}{0.02}} \small = 3×10^{-2} =0.03\)
ここで、電離度\(\alpha\)が\(0.05\)未満なので、\(1-\alpha≒1\)と仮定したのが正しかったというわけです。
もし電離度\(\alpha\)が\(0.05\)より大きくなったときには、先ほど解説したように近似しない式で電離度を求め直す必要があります。
③ \(\rm{[H^+]}\)から\(\rm{pH}\)を求める
まず、\(\rm{[H^+]}\)を求めていきましょう。
\({\rm{[H^+]}} = C \alpha=\sqrt{CK_a}=\sqrt{1.8×10^{-5}×0.020}=6.0×10^{-4}\ \rm{mol/L}\)
以上から、
\(\rm{pH=-log_{10}[H^+] = -log_{10}(6.0×10^{-4})=4-log_{10}2-log_{10}3=3.22}\)
答え:\(\rm{pH=3.22}\)
より実践的な問題はこちらの記事で徹底解説しているので、ぜひこちらもご覧ください。



コメント