今回は,[H+]計算の2回目となります!
前回は強酸について学習しましたね!
今回は1価の弱酸について説明していきますが,強酸での学習が基礎となります.
なので,まだ強酸について読んでいない方はぜひ読んでみて下さい!
[H+]計算を完全マスター!①
それでは,今日も頑張っていきましょう!!
弱酸(1価)
弱酸(1価)・(近似解)
まずは,1価の弱酸の近似解の場合について考えていきます.
まず,近似解で\([\rm{H}^+]\)を求めてみましょう.
\([\rm{H}^+] = \sqrt{0.10 × 2.0 × 10^{-5}} = 1.4 × 10^{-3}\ \rm{mol/L}\)
ここで,確認してほしいことがあります!
全体に対する\([\rm{H}^+]\)の割合がどのくらいかということです!
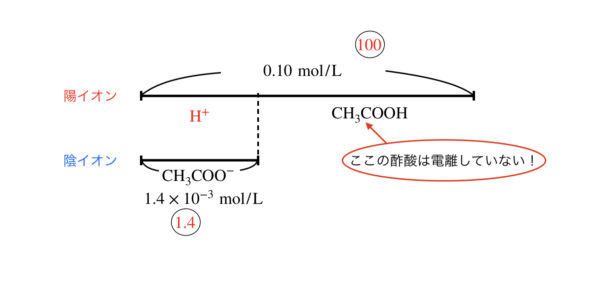
今回の場合であれば,全体:\([\rm{H}^+] = 0.10:1.4 × 10^{-3} = 100:1.4 \)
となりますね!
ここが,\(100:5\)以上であれば,近似解を使うことはできません!!
ここは難しい問題になれば大事になってきますので,問題を解いたときに確認してください!
弱酸(1価)・(厳密解)
厳密解を使わなければならないのは,全体:\([\rm{H}^+] = 100:5 \)以上となるパターンの問題です.
そのような例について考えていきましょう!
まずは近似解を使って求めてみましょう!
\([\rm{H}^+] = \sqrt{0.020 × 2.0 × 10^{-4}} = 2.0 × 10^{-3}\ \rm{mol/L}\)
となります.
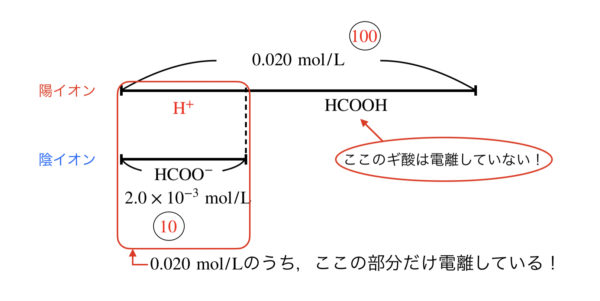
今回の場合は,全体:\([\rm{H}^+] = 0.020:2.0 × 10^{-3} = 100:10 \)
となります.
このため,全体:\([\rm{H}^+] = 100:5\)以上となるので,厳密解を用いなければなりません.
そこで,\([\rm{H}^+] = \) \(x\ \rm{mol/L}\)とすると,\([\rm{HCOOH}] =\) \(0.020\ – x\ \rm{mol/L}\)となります.
今の状態を図にすると,下のようになりますね.
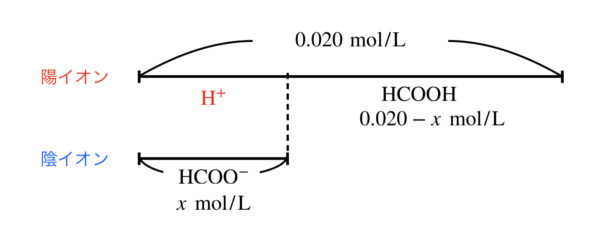
これを\(K_{\rm{a}}\)に代入します.
\(K_{\rm{a}} = \large \frac{[\rm{HCOO}^-][\rm{H}^+]}{[\rm{HCOOH}]} = \frac{x^2}{0.020\ – x} = \normalsize 2.0 × 10^{-4} \)
この2次方程式を解いていきます.
\(x^2 + 2.0 × 10^{-4} – 4.0 × 10^{-6} = 0\)
これを解の公式で解くと,
\(x = [\rm{H}^+] = 1.9 × 10^{-3}\ \rm{mol/L}\)
となります.
1価の弱酸はここまでです!
厳密解を使う場合については,計算も複雑で間違いやすいので,しっかりと復習して確実に解けるようにしてくださいね!!
では,次回は2価の弱酸について詳しく解説していきます!!
今日もお疲れ様です!!



コメント