
結合エネルギーなどは,エネルギー図を使わないと解くのに非常に時間がかかります…
今日も基礎からしっかりと理解していきましょう!
結合エネルギー
今回は,反応熱の応用問題ということで,まずは結合エネルギーの値を使った問題について解説していきましょう!
\(\rm{C-C:345\ kJ/mol,C=C:609\ kJ/mol,C-H:413\ kJ/mol}\)
\(Q_1,Q_2\)を求めよ.
(\(1\))\(\rm{H_2(g)\ +\ Cl_2(g)\ =\ 2HCl(g)\ +\ }\)\(Q_1\ \rm{kJ}\)
(\(2\))\(\rm{CH_2=CH_2(g)\ +\ H_2(g)\ =\ CH_3CH_3(g)\ +\ }\)\(Q_2\ \rm{kJ}\)
(\(1\))
今回の状況を図にすると,下のようになります.
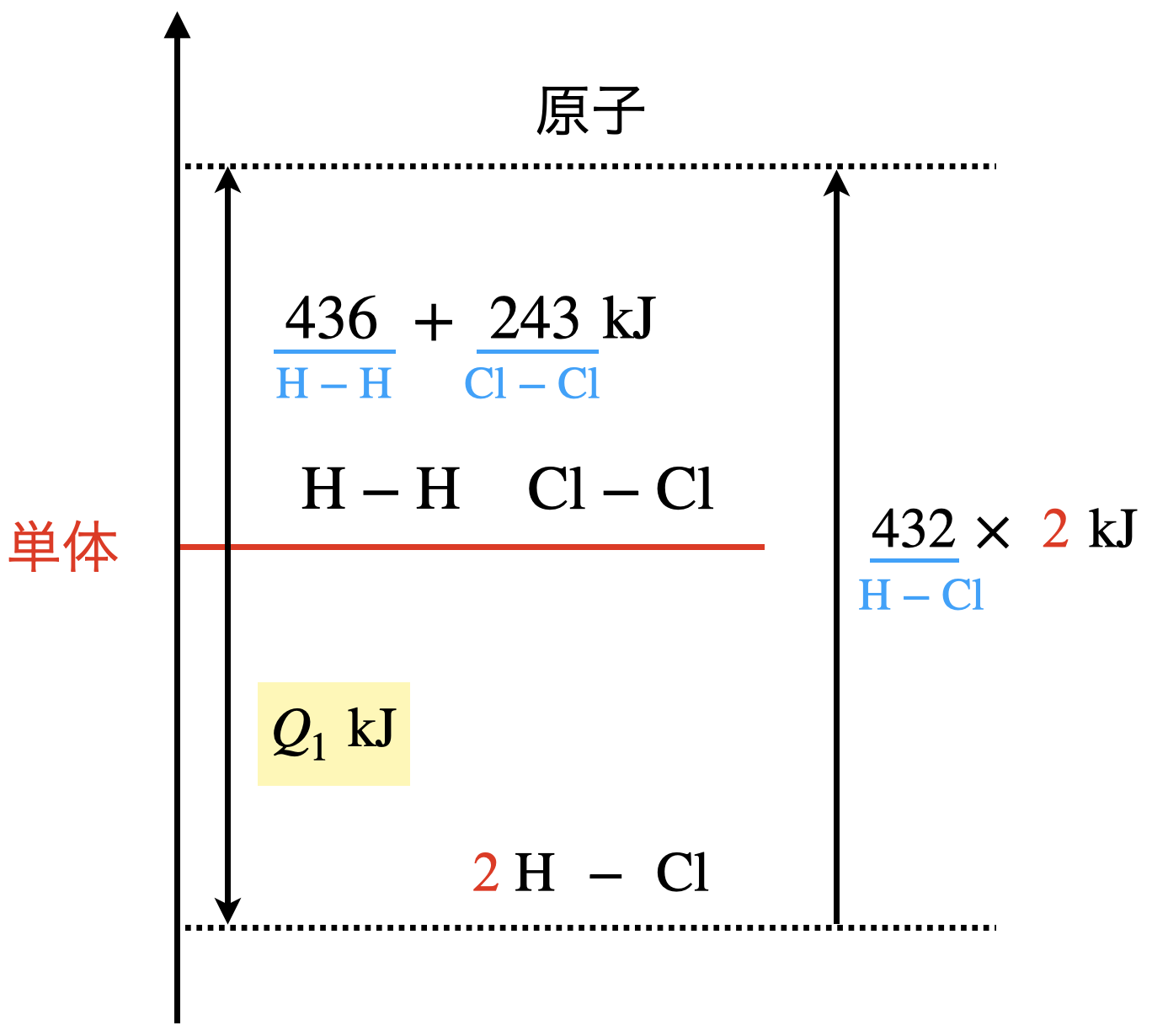
結合エネルギーを求める場合も単体を基準とすることは変わりませんよ!
結合エネルギーを求める場合のポイントは下のようになります.
・反応に出てくる物質を結合を用いて書く.
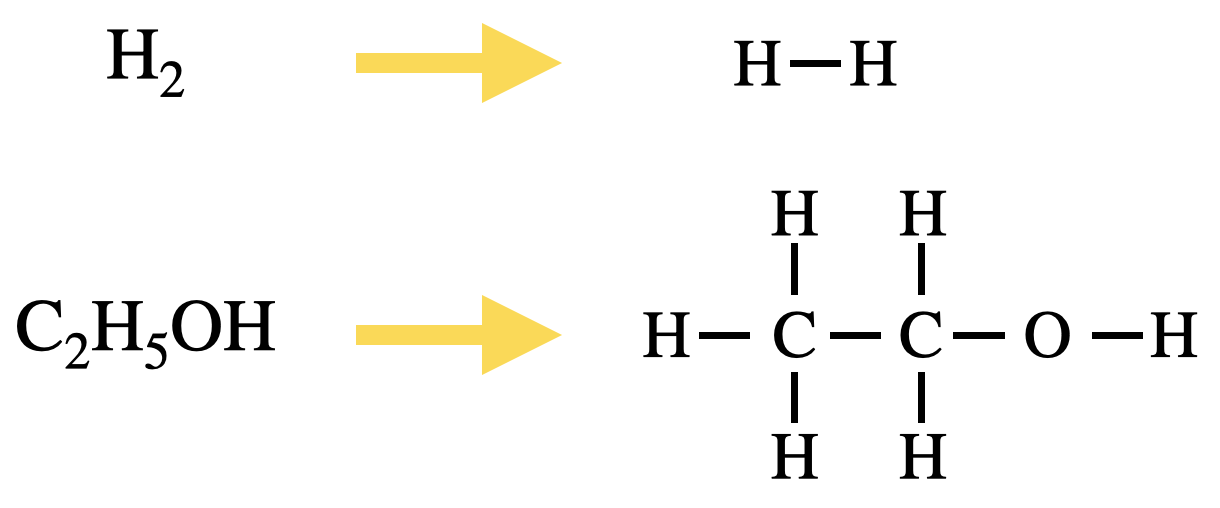
このようにすることで,どの物質とどの物質が結合しているのかを目で確認することができ,ミスを防ぐことができます!
図を書くことができれば,\(Q_1\)はすぐに求めることができますね!
\(436\ +\ 243\ +\ Q_1\ =\ 432\ ×\ 2 \)
\(Q_1\ =\ 185\ \rm{kJ/mol}\)
(\(2\))
今回の問題は(\(1\))より出てくる物質が複雑ですが,各物質の結合を意識すれば確実に解くことができます!
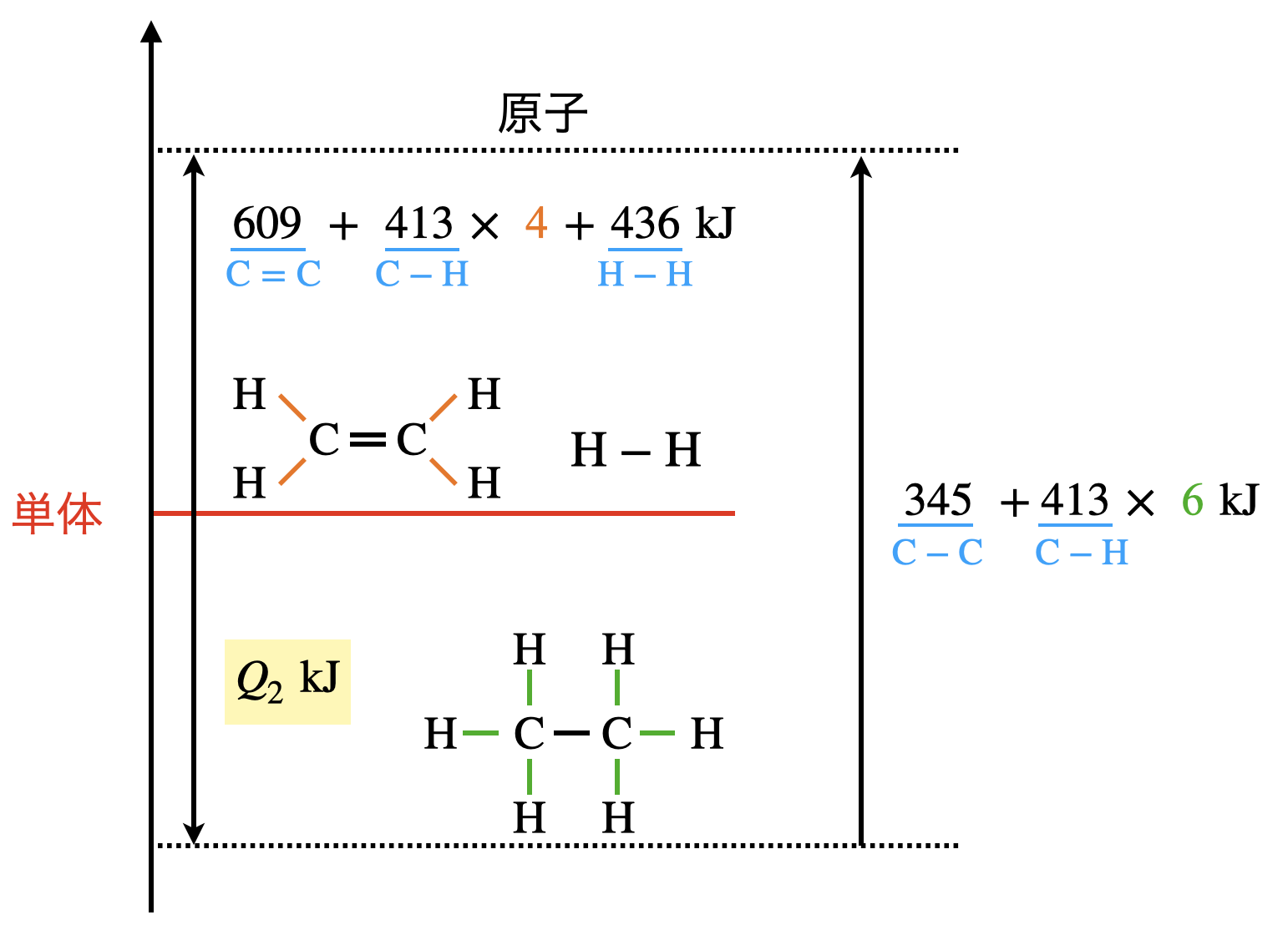
\(609\ +\ 413\ ×\ 4\ +\ 436\ +\ Q_2\ =\ 345\ +\ 413\ ×\ 6\)
\(Q_2\ =\ 126\ \rm{kJ/mol}\)
上の計算では,受験の緊張感では私ならば計算間違いしてしまいます…
この問題はもう少し簡単にすることで,計算を簡略化することができます!その解き方を解説していきましょう!
【別解】
先程の図を見ると,反応の前後で結合が変化していないものもあります.結合が変化していないのであれば,結合エネルギーも必ず変わっていないため,計算する必要はありません.
この問題でいくと,反応の前後で\(\rm{C-H}\)の結合4つは変化していないため,これらの結合については考える必要はありません.
これをわかりやすく図にすると,下のようになります.
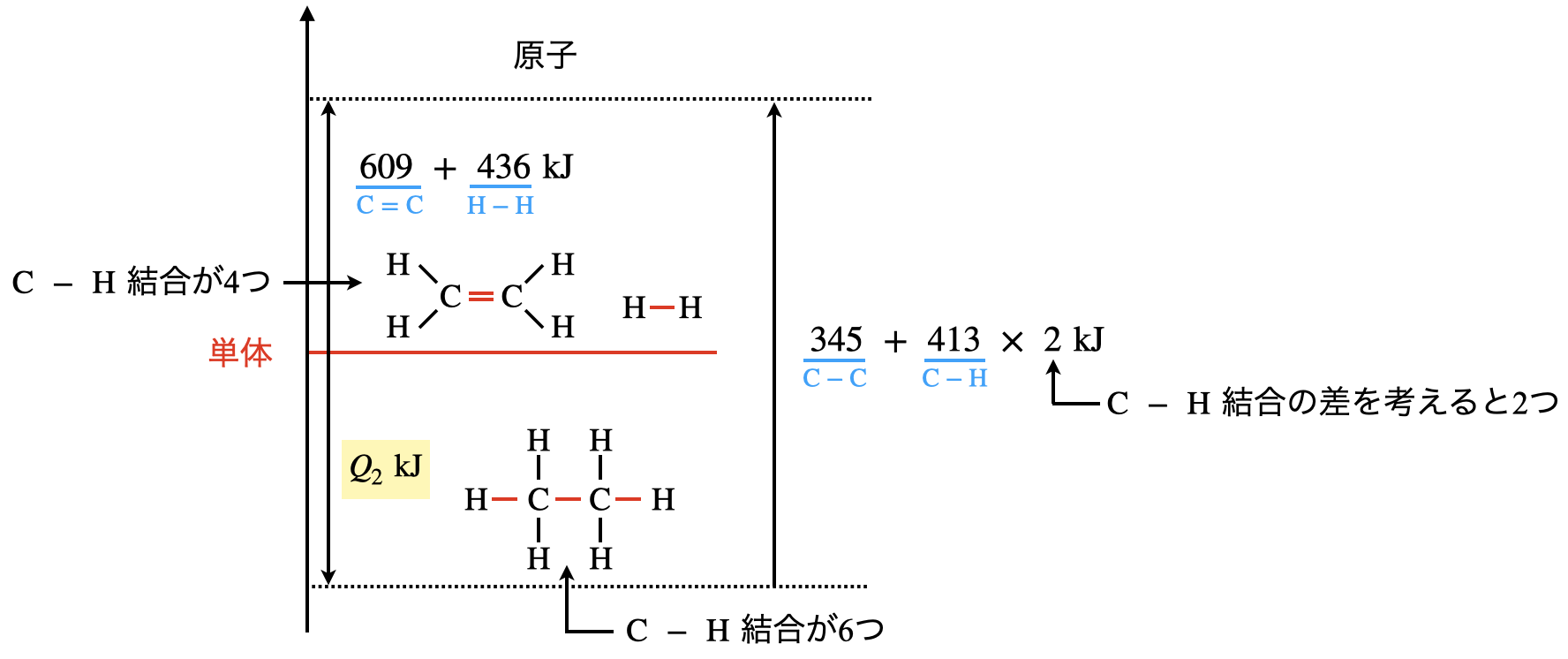
図のように変化した結合だけを色分けすると,非常にわかりやすくなります!
\(609\ +\ 436\ +\ Q_2\ =\ 345\ +\ 413\ ×\ 2\)
\(Q_2\ =\ 126\ \rm{kJ/mol}\)
当然答えは同じになりますが,こちらの方が簡単に計算できました!
このような工夫は少しずつ自分のものにしていってください!!
格子エネルギー
それでは次に,格子エネルギーを求めていきましょう!
今回も解き方は同じですので,安心してください!
\(\rm{Na_{(g)}}\)のイオン化エネルギー:\(496\ \rm{kJ/mol,Na_{(s)}}\)の昇華熱:\(109\ \rm{kJ/mol},\)
\(\rm{Cl_{(g)}}\)の電子親和力:\(347\ \rm{kJ/mol,Cl_2}\)の結合エネルギー:\(243\ \rm{kJ/mol,NaCl_{(s)}}\)の生成熱:\(411\ \rm{kJ/mol}\)
この場合,以下の\(Q\ \rm{kJ/mol}\)を求めよ.
\(\rm{NaCl_{(s)}\ =\ Na^+_{(g)}\ +\ Cl^-_{(g)}}\ -\ \)\(Q\ \rm{kJ}\)
今回は各エネルギーが与えられているだけのなので,それぞれの値がどこの値であるのかを把握しておく必要があります.
下の図で確認してみてください!

このような問題と遭遇すると,上の図を完璧に覚えていることが非常に力を発揮します.この図をもとに,今回の問題を考えていきましょう!
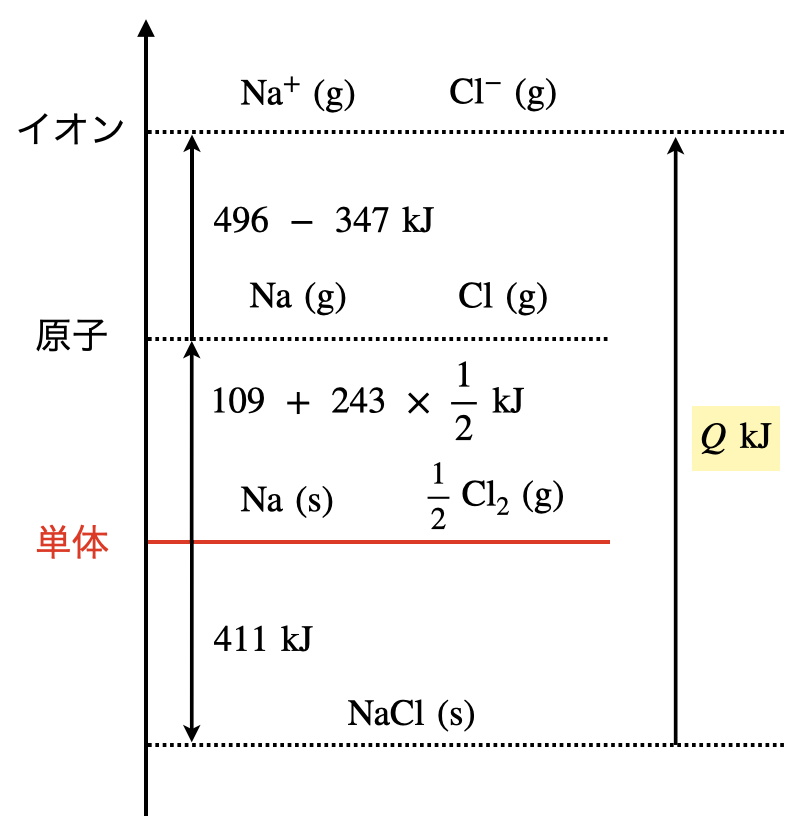
この図を書く順番を説明していきましょう.
①化合物・(陽)イオン
まず与えられた式に出てくる物質の\(\rm{NaCl(s),Na^+(g),Cl^-(g)}\)をエネルギー図上に書きます.
\(\rm{Cl^-(g)}\)は陰イオンですが,便宜上陽イオンの場所に書いています.
この部分については,後ほど説明していきますね.
②単体
エネルギー図で一番大切な単体について考えます.
今回は,\(\rm{Na(s),\large \frac{1}{2} \small Cl_2(g)}\)となります.
③原子
最後に単体と陽イオンから原子を書きます.
今回は,\(\rm{Na(g),Cl(g)}\)となります.
それでは,次にそれぞれの物質間の値について考えていきましょう!
❶単体→化合物
単体→化合物への移動は\(\rm{NaCl_{(s)}}\)の生成熱であるため,\(411\ \rm{kJ/mol}\)となります.
❷単体→原子
それぞれの原子について分けて考えていきましょう!
・\(\rm{Na}\)
\(\rm{Na}\)は固体→気体と変化しており,この状態変化を昇華といいます.
そのため,昇華熱の\(109\ \rm{kJ/mol}\)となります.
・\(\rm{Cl_2(g)}\)
\(\rm{Cl_2(g)}\)については,気体→気体であるため状態変化はありません.
また,\(\rm{Cl-Cl}\) が\(\rm{Cl}\)と変化しているため,\(\rm{Cl_2(g)}\)の結合エネルギーであることがわかります.
今回は,\( \large \frac{1}{2} \small \rm{Cl_2}\)と\(\rm{Cl_2}\)の半分であるため,(結合エネルギー)\(\ ×\ \large \frac{1}{2}\)となります.
❸原子→陽イオン
ここが一番難しいのでしっかりとついてきてくださいね!
・\(\rm{Na^+}\)
\(\rm{Na_{(g)}\ →\ Na^+}\)(原子→陽イオン)であるため,\(\rm{Na}\)の結合エネルギーとなり,\(496\ \rm{kJ/mol}\)となります.
こちらの方は簡単ですが,\(\rm{Cl^-}\)が少し厄介です.
・\(\rm{Cl^-}\)
\(\rm{Cl_2\ →\ Cl_{(g)}}\)(原子→陰イオン)への変化は電子親和力となるので,これは今までに解説してきたものとは少し異なります.
下にまとめてみました!
\(\rm{Cl(g)\ +\ e^-\ →\ Cl^-(g)}\)(原子→陰イオン)への変化は電子親和力となります.これは〇〇熱でもなく,〇〇エネルギーでもありません.電子親和力は電子親和「熱」として考えてください!
つまり電子親和力は「発熱反応」となります.
\(\rm{Cl}\)は電子をもらうことで,最外殻電子が全てうまるため安定化します!
そのため,陽イオンと合わせて考えるためには,以下のような手順を行います.
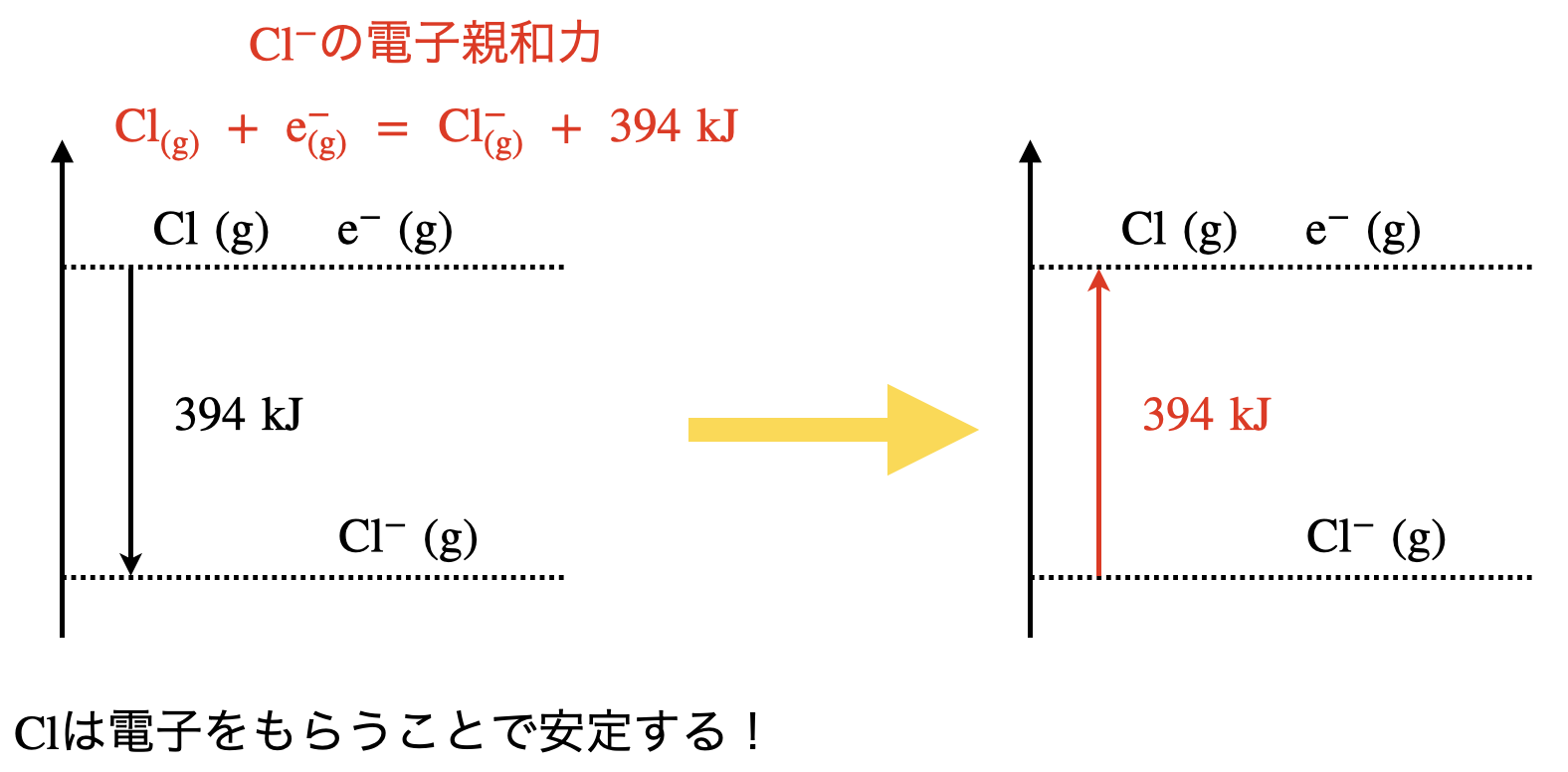
以上から,\(Q\)を求めることができます.
\(Q\ =\ 411\ +\ (109\ +\ 243\ ×\ \large \frac{1}{2} \small )\ +\ (496\ -\ 347)\ =\ 790.5\ \rm{kJ/mol}\)
今回は出てくる物質が多く,少し難しく感じたかもしれません.
また,陰イオンにおける電子親和力も初めて扱ったため,戸惑いを感じてしまったかもしれません.
この辺は非常に難しいですが,この問題が解けるようになると,確実に周りと差をつけられるようになるため,一緒に頑張っていきましょう!
熱化学方程式を書いていては,非常に複雑になってしまいます…



コメント