
今回は物質量の計算方法について初学者に向けて徹底解説していきます.
- 物質量って結局どういう概念なの?
- 物質量を使った実際の計算方法とは?
を特にポイントとしています.昨日の自分より少しでもレベルアップしていきましょう!
本サイトでは,イラストや例えを多く用いて初学者にも分かりやすいように解説しています.もっと分かりやすく解説してほしいという部分がありましたら,遠慮なくブログのコメントかTwitter(chem_story1)までご連絡ください!
物質量ってなに?
高校化学を勉強するにあたり,一番化学嫌いを生み出すのが「\(\rm{mol}\)」という概念だと思います.今日はこの「\(\rm{mol}\)」について徹底解説して,少しでも苦手意識をなくしていきましょう.
「\(\rm{mol}\)」は,化学を学習するにあたり最重要の単位です.そして\(\rm{1\ mol}\)というのは,ある原子・分子を\(6.02 × 10^{23}\)個集めた状態を表します.
例えば,炭素原子が\(\rm{1\ mol}\)あるということは,炭素原子が\(6.02 × 10^{23}\)個存在する,ということを意味しています.そして\(\rm{1\ mol}\)あたりの粒子数の基本である\(6.02 × 10^{23}\)をアボガドロ定数(\(N_{\rm{A}}\))といいます.この値は問題に与えられるため,覚える必要はありませんよ!
物質量を考える理由
「\(\rm{mol}\)」という単位を受け入れるためには,なぜこの単位を使う必要があるのか?ということも理解しておく必要があるでしょう.
その理由は,原子がとても小さいからです.
原子が小さすぎると,目で数えることはできませんよね.しかしながら,多くの原子が集まると,今度は逆に数えにくくなります.そこで折衷案として,「\(\rm{mol}\)」という単位が生まれました.「\(\rm{mol}\)」という単位を使って,\(6.02 × 10^{23}\)個を\(1\)かたまりとして数えることで,小さな原子が数えやすくなりました.
「\(\rm{mol}\)」を使う→\(\ 6.02 × 10^{23}\)個という膨大な粒子を\(1\)かたまりとして数えることができる
原子量・モル質量って?
「\(\rm{mol}\)」の定義は,ある原子・分子が\(6.02 × 10^{23}\)個集まった状態だと解説しました.この\(6.02 × 10^{23}\)という値は,炭素原子を\(\rm{12\ g}\)集めたときの粒子数がこの値だったため,この値を使うようになりました.つまり,\(\rm{1\ mol}\)の炭素原子\(\rm{\ =12\ g}\)の炭素原子ということになります.
この\(12\)という値が「原子量」というものです.つまり原子量とは,\(\rm{1 mol}\)あたりの各原子の質量ということになります.原子量に単位はありませんが,原子量に単位をつけたものがモル質量 \(\rm{[g/mol]}\)といいます.
ややこしいので,下にまとめておきます.
原子量 \([-] =\) モル質量 \(\rm{[g/mol]}\)
※原子量は単位はないが,モル質量には単位がある.原子量とモル質量は同じ値である.
この原子量については,各物質によって変化しますが,テストなどでは問題文に与えられているため暗記する必要はありませんよ!
モルBOX
物質量の意義は理解できたと思いますが,次は実際に「\(\rm{mol}\)」を使う際の考え方について解説していきます.まず,物質量を求めるには以下の式で求めることができます.
\(\rm{物質量\ [mol] = \large \frac{質量\ [g]}{モル質量\ [g/mol]}}\)
そしてこの\(\rm{mol}\)を,私は「モルBOX」という箱として考えています.
どういうことかというと,今山積みの原子が存在するとします.ここには多くの原子が存在しているので,簡単に数えることはできません.そこで,モルBOXを使って一定量ずつ原子を箱の中に入れていきます.
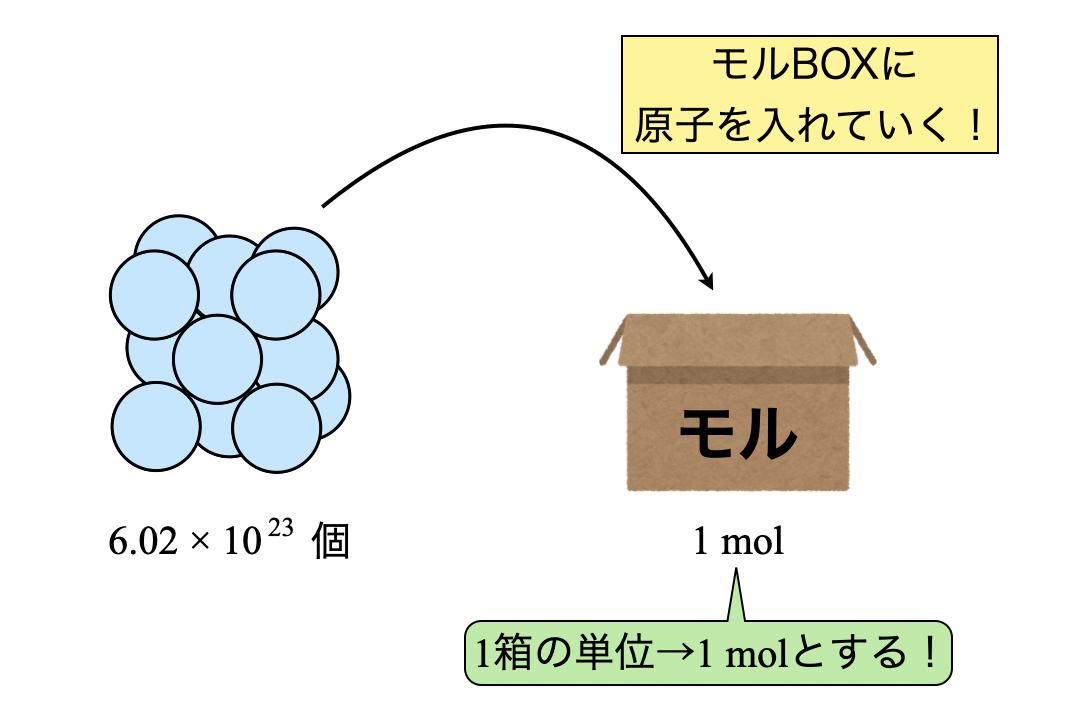
このとき,\(1\)箱を\(\rm{1\ mol}\)とカウントしているのです!そしてこのモルボックスにはさらに重要な点が\(2\)つあります.
①モルBOXの体積
\(1\)つ目は,モルBOXの体積です.これは\(\rm{22.4\ L}\)と決まっています.どの原子の箱であっても変わらないことを覚えておいてくださいね!
②モルBOXの粒子数
\(2\)つ目は,モルBOX\(1\)箱に入る原子の粒子数です.これも\(6.02 × 10^{23}\)個であると決まっています.これもどの原子のどの箱であっても変わりません.
つまりこのモルBOXという魔法の箱を使うと,異なる原子間を考えたり,\(\rm{g ⇄ L ⇄\ }\)個数といった単位の変換を行うことも簡単になります.
ここでモルBOXについて\(1\)つ注意点があります.それはモルBOXの質量は原子ごとに違うということです.これは粒子\(1\)個あたりの質量が違うので,\(1\)箱に入る粒子数が同じでも質量は異なるというわけです.
モルBOXの凄さを理解していただけましたか?
まだ半信半疑な部分があると思うので,実際の計算方法を解説しながらさらに理解を深めていきましょう.

- 粒子数→変化なし
- 体積→変化なし
- 質量→物質による
物質量を使った実際の計算方法
実際の計算方法を理解するにあたり,下の三角形を覚えましょう.そしてこの三角形の真ん中にモルBOXを置き,そのモルBOXを介してそれぞれの値を求めていきます.
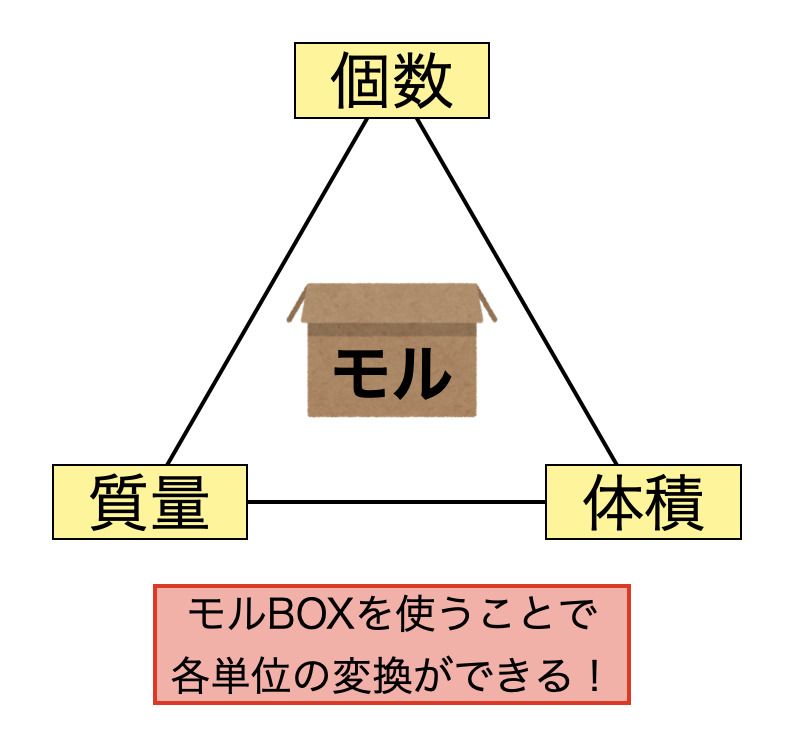
ここの計算で\(1\)つ大切なことがあるので,説明しておきます.それはある単位からモルBOXに乗せるときには\(÷\),モルBOXから各単位に変換させるときには\(×\)をします.
- 単位→モルBOXのとき,\(÷\)
- モルBOX→単位のとき,\(×\)
このテンプレートを実際の問題で使いこなしていきましょう.
二酸化炭素が\(\rm{1.1\ g}\)ある.原子量は\(\rm{C=12}\),\(\rm{O=16}\)とする.
(\(1\))このとき物質量は何\(\rm{mol}\)か?
(\(2\))このとき,標準状態で体積は何\(\rm{L}\)か?
(\(3\))この中には何個の二酸化炭素分子が含まれているか?
(\(4\))この中には炭素原子と酸素原子あわせて何個存在するか?
質量 → モルBOX
(\(1\))質量からモルBOXに変換するので,分子量で割れば\(\rm{OK}\)です.今回の関係を図にすると下のようになります.
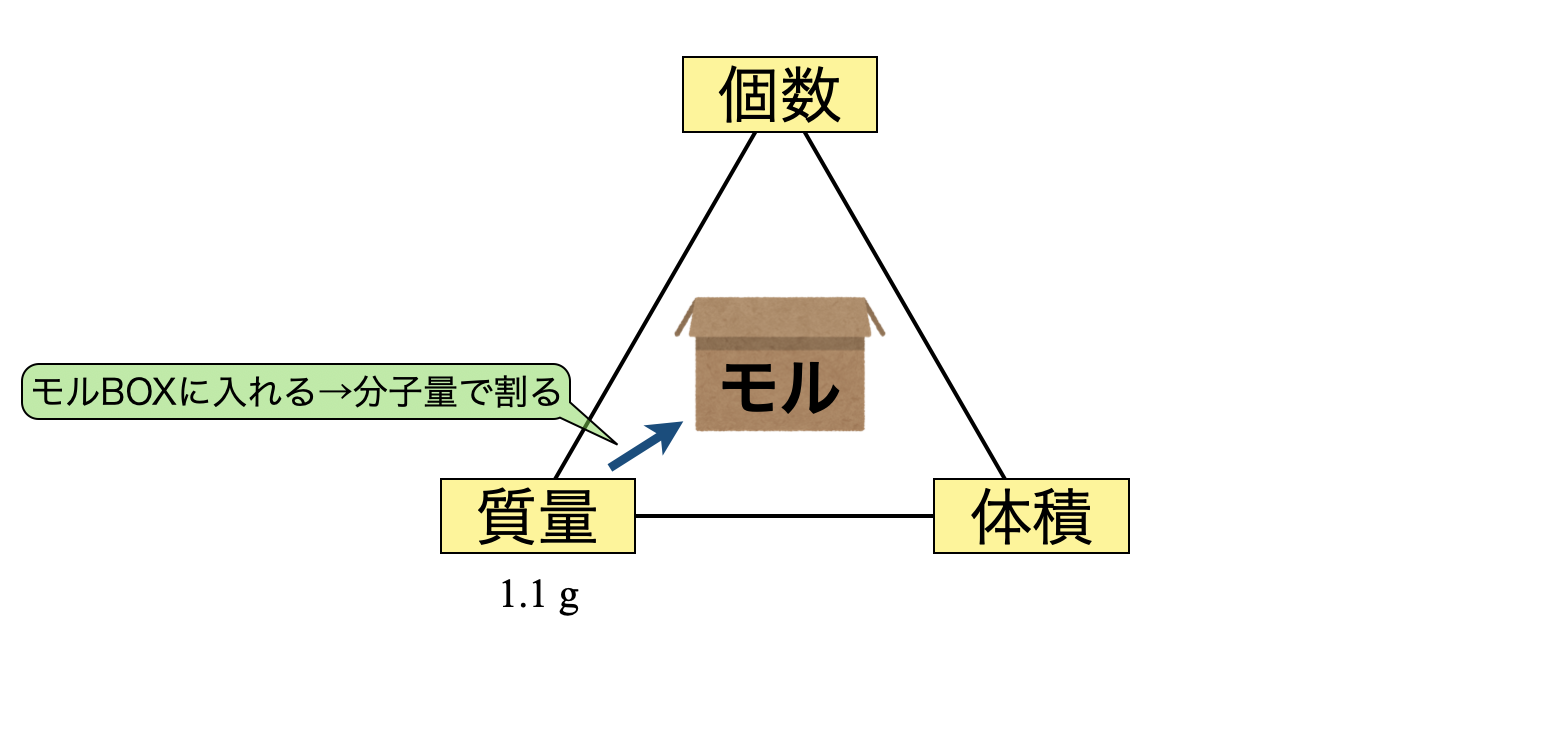
物質量 \(\rm{= \large \frac{1.1}{44} \small = 0.025\ mol}\)
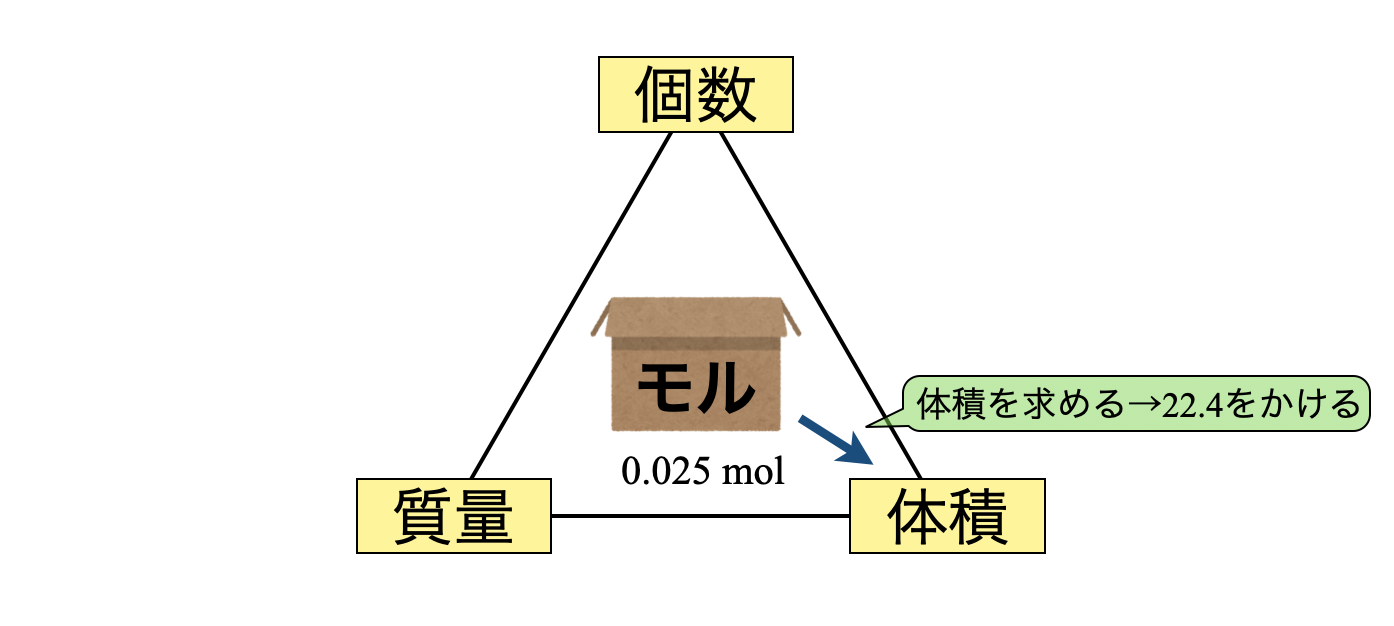
モルBOX → 体積
(\(2\))モルBOXから体積に変換します.モルBOX\(1\)箱あたりの体積は\(\rm{22.4\ L}\)でした.この値は必ず覚えてくださいね!
体積 \(\rm{ = 0.025 × 22.4 = 0.56\ L}\)
モルBOX → 個数
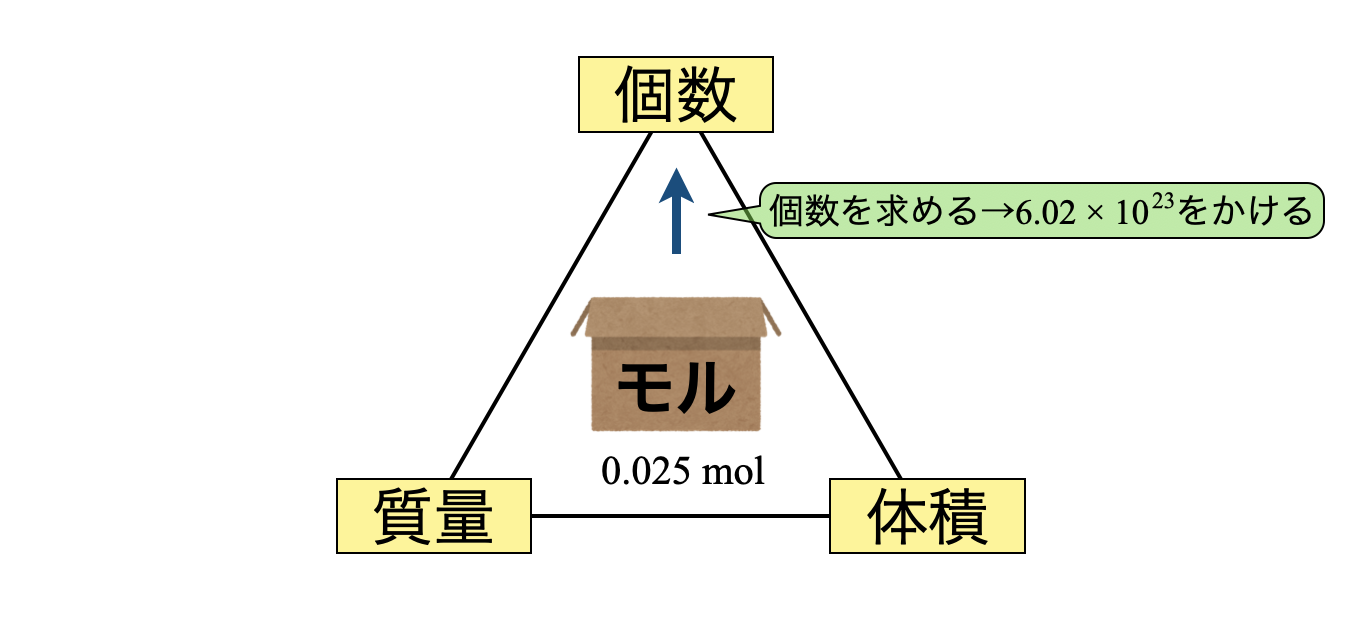
(\(3\))モルBOXから個数に変換します.モルBOX\(1\)箱あたりの粒子数は\(6.02 × 10^{23}\)個です.この値も物質によって変化しません.
粒子数 \(= 0.025 × 6.02 × 10^{23} = 0.15 × 10^{23} = 1.5 × 10^{22}\ \)個
炭素原子と酸素原子をあわせた粒子数
(\(4\))炭素原子と酸素原子をあわせた粒子数を考える問題です.これは二酸化炭素分子を原子に分解して考えていきましょう.
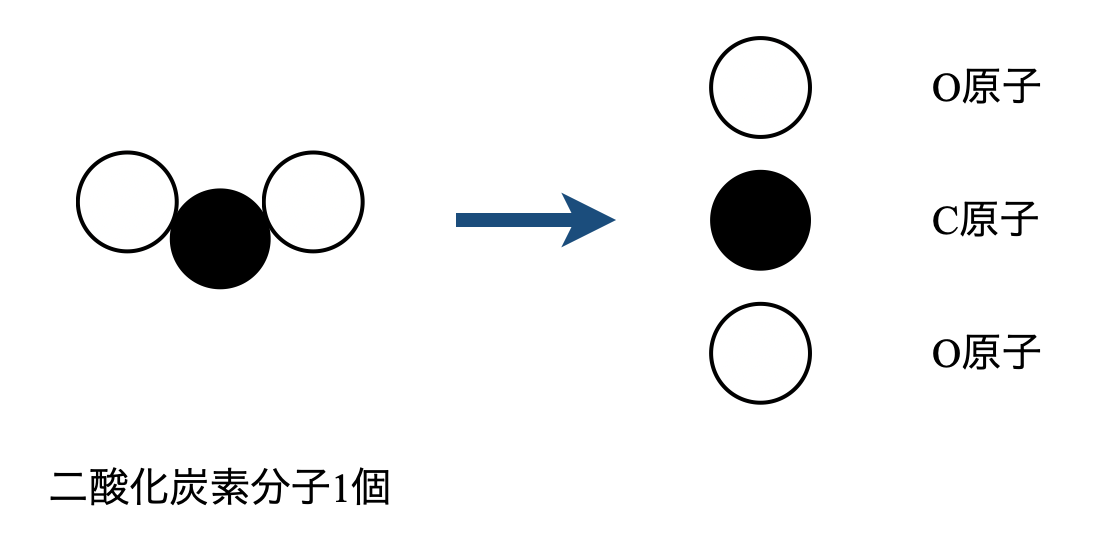
すると,\(1\)つの二酸化炭素分子から炭素原子\(1\)個,酸素原子\(2\)個の合計\(3\)個が生成していることがわかります.そのため(\(3\))で求めた粒子数の\(3\)倍が炭素原子と酸素原子をあわせた粒子数になります.
炭素原子と酸素原子をあわせた粒子数 \(= 1.5 × 10^{22} × 3 = 4.5 × 10^{22}\ \)個
モルBOXを使うことで断然正答率が上がり,頭もスッキリすると思います.この考え方は反応式の分野でも応用できるので,しっかりと使いこなせるようにしていきましょう.
これからも皆さんのためになるような記事を発信していきます!よければ\(\rm{Twitter}\)(chem_story1)のフォローもお願いしますね!



コメント