今回のメニューです。
✅個数と物質量の関係
✅質量数と物質量の関係
✅体積と物質量の関係
今回の記事を読んでいただくと、化学で最重要な物質量(\(\rm{mol}\))について完全理解することができます。
最後まで丁寧に解説していくので、ぜひ最後までご覧ください!
また、わからないことはぜひコメント欄までお願いします。
解説してほしい分野があればぜひ次の記事のコメント欄で教えてくださいね!

私はYouTubeでも高校化学の解説をしているので、ぜひそちらもご覧ください。
物質量(mol)とは?
\(6.0×10^{23}\)個の粒子の集団を\(\rm{1\ mol}\)といいます。
物質量(\(\rm{mol}\))とは個数を数えるときに使うただの単位です。
\(6.0×10^{23}\)の単位を見てみましょう。
参考書を見ると、「\(\rm{/mol}\)」と書かれていることがよくありますが、
丁寧に書くと、これは「\(\rm{コ/mol}\)」という意味です。
つまり、\(\rm{1\ mol}\)あたりに\(6.0×10^{23}\)コの原子があるよ!っという意味になることがわかります。
なので、\(6.0×10^{23}\)は、個数をモルに変換する変換キーととらえましょう。
\(\rm{1\ mol=6.0×10^{23}}\)個なので、\(\rm{6.0×10^{23}\ コ/mol}\)で考える。
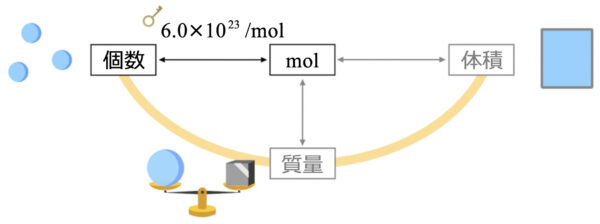
個数と物質量の関係
では、先ほどから説明している\(6.0×10^{23}\)という値に関して解説していきます。
質量数\(12\)の炭素(\(\rm{^{12}C}\))を一粒一粒天秤に乗せて質量を測ることとします。
すると、質量数\(12\)の\(\rm{^{12}C}\)がちょうどピッタリ\(\rm{12\ g}\)になったときの個数が\(6.0×10^{23}\) 個だったのです。
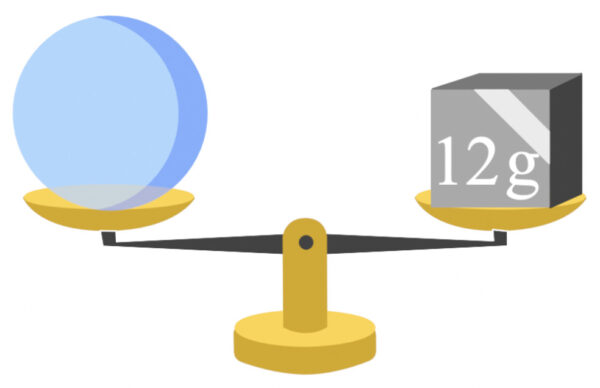
つまり、これは質量数と同じ\(\rm{g}\)になったときの個数が\(6.0×10^{23}\) 個ということです。
そして、原子を数えるときに、\(6.0×10^{23}\)では数えにくいので、これを\(\rm{1\ mol}\)という新しい単位に置き換えることにしました。
なので、単位はコを省略して、\(\rm{6.0×10^{23}\ /mol}\)となります。
ただ、実際の問題を考えるときには、単位を\(\rm{コ/mol}\)とした方が断然わかりやすいので、
私はいつも「\(\rm{コ/mol}\)」で考えています。
なので、問題を解くときのポイントは、このような図をイメージすることです。
そして\(\rm{mol}\)と個数をやり取りするときは、\(6.0×10^{23}\)という変換キーを使いましょう。
質量と物質量の関係
では次に、質量と物質量の関係を見ていきましょう。
今回は例として、\(\rm{H}\)、\(\rm{C}\)、\(\rm{O}\)原子を考えていきます。
まず、それぞれの原子の絶対質量、すなわち原子の質量を測ります。
ただこれでは計算しにくいので、それぞれの原子の質量の比、すなわち相対質量を考えていきます。
すると、\(\rm{H}\):\(\rm{C}\):\(\rm{O}\)の比は\(1:12:16\)になります。
ここまでは相対質量の復習です。
|
原子
|
絶対質量 \(\rm{[g]}\)
|
相対質量
|
|
\(\rm{^1H}\)
|
\(1.6735×10^{-24}\)
|
\(1.0078\)
|
|
\(\rm{^{12}C}\)
|
\(1.9926×10^{-23}\)
|
\(12\)
|
|
\(\rm{^{16}O}\)
|
\(2.6560×10^{-23}\)
|
\(15.995\)
|
では次に、各原子を\(6.0×10^{23}\) 個まとめた際の質量を計算してみましょう。
\(\rm{H}\)原子:\(\rm{1.6735×10^{-24}×6.0×10^{23}=1.0041\ g≒1\ g}\)
\(\rm{C}\)原子:\(\rm{1.9926×10^{-23}×6.0×10^{23}=11.9556\ g≒12\ g}\)
\(\rm{O}\)原子:\(\rm{2.6560×10^{-23}×6.0×10^{23}=15.936\ g≒16\ g}\)
ここで先ほど解説したように、\(6.0×10^{23}\) 個は\(\rm{1\ mol}\)なので、この質量は\(\rm{1\ mol}\)あたりの質量ということになります。
この値をモル質量 \(\rm{[g/mol]}\)といいます。単位を見ると、\(\rm{1\ mol}\)あたりが何 \(\rm{g}\)かということを表していることがわかります。
|
原子
|
絶対質量 \(\rm{[g]}\)
|
\(\rm{1\ mol}\)あたりの質量 \(\rm{[g]}\)
|
|
\(\rm{^1H}\)
|
\(1.6735×10^{-24}\)
|
\(1\)
|
|
\(\rm{^{12}C}\)
|
\(1.9926×10^{-23}\)
|
\(12\)
|
|
\(\rm{^{16}O}\)
|
\(2.6560×10^{-23}\)
|
\(16\)
|
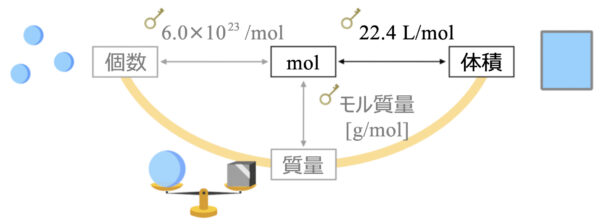
では、先ほどの図に質量を加えていきましょう。
質量から物質量に変換するときの変換キーはモル質量になります。
そして、モル質量は原子量や分子量、式量と同じ値なので新たに覚え直す必要はありませんよ。
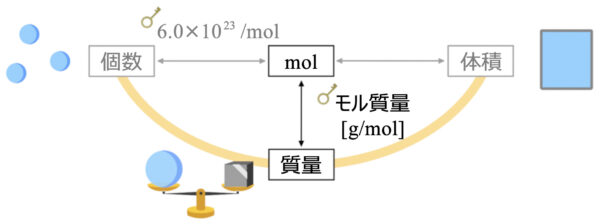
質量と物質量の変換キー:モル質量
原子量や分子量、式量が苦手な方は、ぜひこちらの記事をご覧ください!

体積と物質量の関係
気体の体積もわかりやすく考えることができます。
気体分子をある箱の中に\(6.0×10^{23}\) 個、つまり\(\rm{1\ mol}\)入れたとします。
このとき、標準状態では体積は\(\rm{22.4\ L}\)となります。
ここで標準状態とは、\(\rm{0°C}\)、\(\rm{1.0×10^5\ Pa}\)のときの状態のことです。
この標準状態はこれから重要になるので、しっかりと覚えておきましょう!
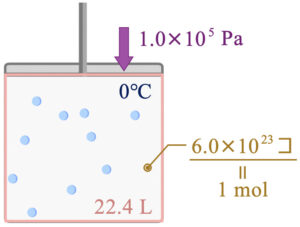
これは分子の種類によらず、同じ値になります。この理由を簡単に説明しておきましょう。
気体の体積を決定するには、温度と圧力が重要な因子になります。
温度
まずは温度です。
気体の種類によって、その分子の大きさは多少の誤差がありますが、分子は激しく動き回っています。
つまり、分子の運動エネルギーによって体積が決まります。
この分子の運動エネルギーは温度の関数なので、温度によって運動エネルギーが決まり、体積が決まるというわけです。

圧力
次は、圧力です。
圧力が高くなると、上から押されるので、体積が小さくなるというのは感覚的にわかると思います。
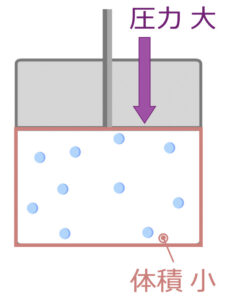
これを総合的に考えると、
気体分子の体積は分子の種類ではなく、温度と圧力によって決定されます。
そのため、体積を表現するときには、それが圧力いくらで、温度が何度かというのが重要な要素になります。
ここでは、もっとも一般的な標準状態(\(\rm{0°C}\)、\(\rm{1.0×10^5\ Pa}\))で考えています。
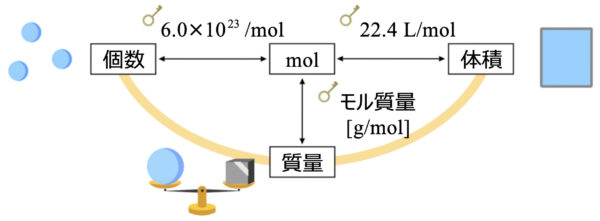
では、先ほどの図に質量を加えていきましょう。
物質量から体積に変換する変換キーは\(22.4\)になります。
体積と物質量の変換キー:\(22.4\)
まとめ
では、最後に物質量(\(\rm{mol}\))と質量、個数、体積の関係をまとめておきましょう。
この図を覚えておくと、モル計算はどんな問題でも解くことができるので、しっかりと覚えておいてくださいね!
私はYouTubeでも高校化学の解説をしているので、ぜひそちらもご覧ください。



コメント