前回は,溶解度積の基礎と基本的な計算問題について解説していきました!
まだ見ていない方は,こちらの記事(難溶性塩の溶解度積①)を先に読んでいただいた方が,今回の内容をより理解できると思います!
今回はもう少し難易度は上がりますが,頻出の問題を徹底的に詳しく解説していきますので,最後まで私についてきて下さい!
今回は図も利用して視覚的に理解できるようにしていきます!
溶解度積(計算編②)
では,まず本日の問題を見ていきましょう!
この溶液に\(\rm{Ag^+}\)を徐々に加えていく.
\(\rm{Ag^+}\)を加えることに対する体積変化は無視できるとする.
それぞれの溶解度積は以下の通りである.
\(\rm{AgCl}\)の\(K_{\rm{sp}}\)は\(K_{\rm{sp}}(\rm{AgCl}) = [\rm{Ag^+}][\rm{Cl^-}] = 2.8 × 10^{-10}\ (\rm{mol/L})^2\)
\(\rm{Ag_2CrO_4}\)の\(K_{\rm{sp}}\)は\(K_{\rm{sp}}(\rm{Ag_2CrO_4}) = [\rm{Ag^+}]^2 [\rm{CrO_4^{2-}}] = 2.0 × 10^{-12}\ (\rm{mol/L})^3\)
(\(1\))\(\rm{AgCl}\)と\(\rm{Ag_2CrO_4}\)の沈殿の順番はどのようになるか?
(\(2\))2番目の沈殿が生成したとき,最初の沈殿を作った陰イオンは何\(\%\)沈殿しているか?
(1)
それでは解説していきましょう!
まず,\(\rm{AgCl}\)について考えていきます.
\(\rm{AgCl}\)が沈殿し始めるときの\([\rm{Ag^+}] =\)\( x\ \rm{mol/L}\)を求めていきます!
今求めようとしているところは,下の図の部分になります.
\(x × 0.10 = 2.8 × 10^{-10}\)
\(x = 2.8 × 10^{-9}\ \rm{mol/L}\)
同じようにして,\(\rm{Ag_2CrO_4}\)が沈殿し始めるときの\([\rm{Ag^+}] =\)\( y\ \rm{mol/L}\)を求めていきます!
\(y^2 × 0.020 = 2.0 × 10^{-12}\)
\(y = 1.0 × 10^{-5}\ \rm{mol/L}\)
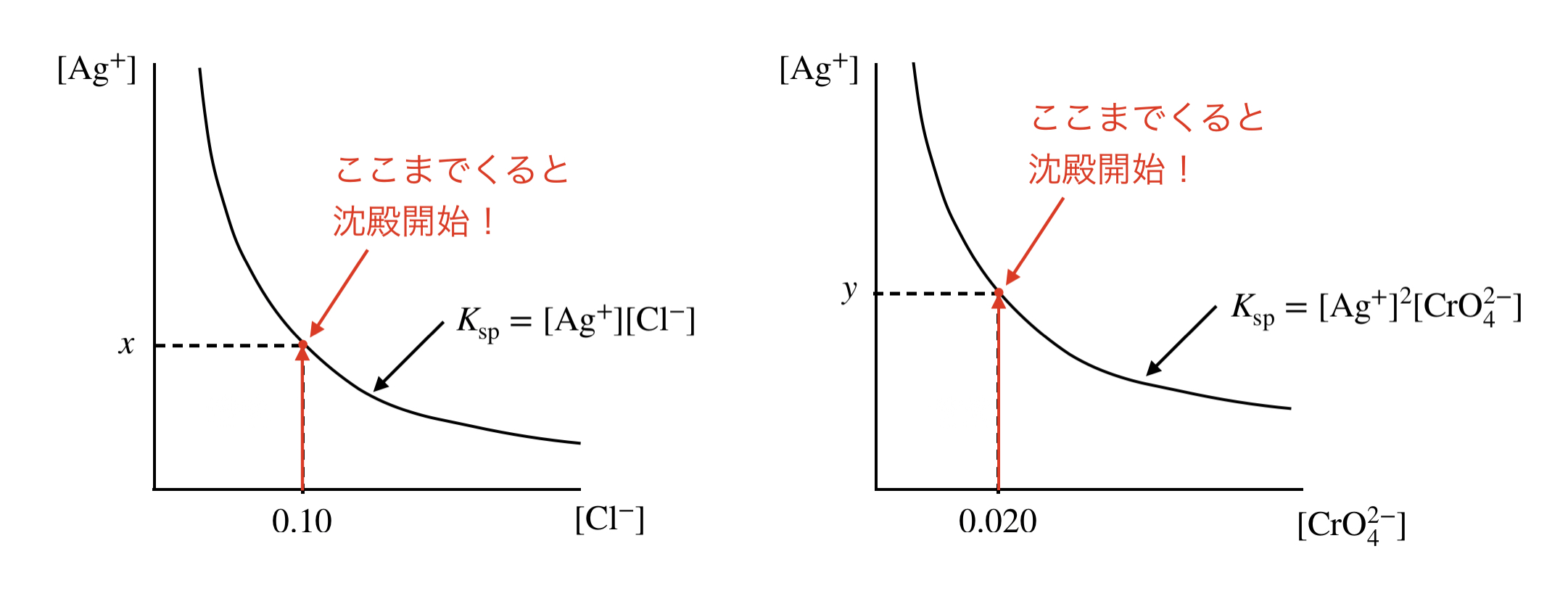
\(x \ll y\)となっているので,\(\rm{AgCl}\)が先に沈殿します!
(\(2\))
\(\rm{Ag_2CrO_4}\)が沈殿するときの\([\rm{Ag^+}]\)は\(1.0 × 10^{-5}\ \rm{mol/L}\)です.
このときの最初の沈殿,すなわち\(\rm{AgCl}\)の場合を図にすると,下のようになります.
図をどんどん書いて,自分で書けるようになることが成績アップのコツですよ!
面倒くさがらずに書いてくださいね!
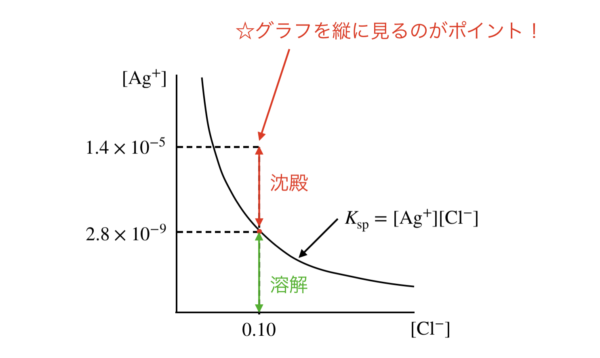
これから沈殿している割合は簡単に求めることができます.
\(\large \frac{1.0 × 10^{-5}\ -\ 2.8 × 10^{-9}}{1.0 × 10^{-5}} \small = 99.972 \%\)
溶解度積(計算編③)
次が最後の問題ですので,しっかり頑張っていきましょう!
Al3+ + 3OH– → Al(OH)3
\(K_{\rm{sp}} = [\rm{Al^{3+}}][\rm{OH^-}]^3 = 1.0 × 10^{-32}\ (\rm{mol/L})^4\)
この溶液にさらに強塩基を加えていくと,白色沈殿が溶解する.
Al(OH)3 + OH– → [Al(OH)4]–
\(K = \large \frac{[\rm{Al(OH)_4^-}]}{[\rm{OH^-}]} \small = 10\)
(\(1\))いま,\(1.0 × 10^{-2}\ \rm{mol/L}\)の塩化アルミニウム水溶液\(1.0\ \rm{L}\)に水酸化ナトリウム水溶液を加えていく.水酸化アルミニウム\(\rm{Al(OH)_3}\)の沈殿が生成し始めるときの\(\rm{pH}\)は?
(\(2\))\(\rm{Al(OH)_3}\)がちょうど全部溶解したときの\(\rm{pH}\)は?
(\(1\))
それでは一緒に解いていきましょう!
いまの\(\rm{Al^{3+}}\)の濃度は,\([\rm{Al^{3+}}] = 1.0 × 10^{-2}\ \rm{mol/L}\)となっています.
下の図を見てほしいのですが,最初は強塩基が全く含まれていないので,①の状態になっています.
そこから強塩基を加えていくと,②までいったところで沈殿が開始します!
先ほどはこの図を縦に見ましたが,今回は横に見ています.
このように縦・横どちらからでも考えていけるように練習していましょう!
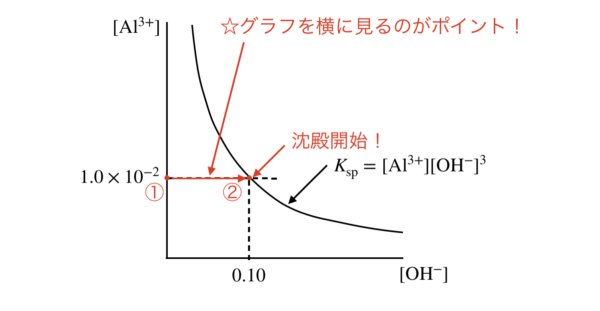
②の状態で\(K_{\rm{sp}} = [\rm{Al^{3+}}][\rm{OH^-}]^3\)の式を用いると,
\((1.0 × 10^{-2}) × [\rm{OH^-}]^3 = 1.0 × 10^{-32}\)
\([\rm{OH^-}] = (1.0 × 10^{-30})^{1/3}\ \rm{mol/L} = 1.0 × 10^{-10}\ \rm{mol/L}\)
となり,すぐに解くことができましたね!
(\(2\))
まずは,\(K = \large \frac{[\rm{Al(OH)_4]^-}}{[\rm{OH^-}]} \small = 10\)について先に少し説明しておきましょう.
Al(OH)3 + OH– → [Al(OH)4]–
上の反応について,平衡定数を考えると,
\(K’ = \large \frac{[\rm{Al(OH)_4]^-}}{[\rm{Al(OH)_3}][\rm{OH^-}]}\)
となります.
ここで\(\rm{Al(OH)_3}(\rm{s})\)は固体であり,水溶液中では一定とみなすことができます.
両辺に\([\rm{Al(OH)_3}]\)をかけ,
\(K = K’ [\rm{Al(OH)_3}] = \large \frac{[\rm{Al(OH)_4]^-}}{[\rm{OH^-}]}\)
と表されています.
本問題では,\(\rm{Al(OH)_3}\)がちょうど溶解したときであるため,\(K = \large \frac{[\rm{Al(OH)_4]^-}}{[\rm{OH^-}]}\)の式を用いることができます.
また\(\rm{Al(OH)_3}\)がすべて溶解したとき,最初の\(\rm{Al^{3+}}\)は\([\rm{Al(OH)_4}]^-\)となっています.
そのため,\([\rm{Al(OH)_4}]^- = 1.0 × 10^{-2}\ \rm{mol/L}\)となります.
これを\(K\)の式に代入すると,
\(K = \large \frac{1.0 × 10^{-2}}{[\rm{OH^-}]} \small = 10\)
\([\rm{OH^-}] = 1.0 × 10^{-3}\ \rm{mol/L}\)
ここからも1つポイントがあります!
\([\rm{OH^-}]\)から\(\rm{pH}\)を求めるときは,\([\rm{OH^-}]→\rm{pOH}→\rm{pH}\)とすると速く解くことができます!
まず\([\rm{OH^-}] = 1.0 × 10^{-3}\ \rm{mol/L}\)から\(\rm{pOH}\)を求めていきます.
\(\rm{pOH} = log_{10}{(1.0 × 10^{-3})} = 3\)となります.
これを\(\rm{pH}\)に変えるために,\(\rm{pH+pOH}=14\)という式を使います!
すると,\(\rm{pH=14-pOH}=14-3=11\)
となり,複雑な計算をせずに求めることができます!
\([\rm{H^+}] = \large \frac{K_{\rm{w}}}{[\rm{OH^-}]}\small = \large \frac{1.0 × 10^{-14}}{1.0 × 10^{-3}} \small = 1.0 × 10^{-11}\)
\(\rm{pH} = log_{10}{(1.0 × 10^{-11})} = 11\)
となります.
\([\rm{H^+}][\rm{OH^-}] = K_{\rm{w}}\)の式を用いると,時間のかかる問題が多いので気をつけましょう!
今日は以上となります!
溶解度積については,グラフを使えるようになるとすぐに溶けるようになるので,しっかりと練習して解けるようにしてくださいね!



コメント