
蒸気圧降下・沸点上昇・凝固点降下・浸透圧の\(4\)大特徴を理解するときのポイントを先にお伝えしておきます!
ズバリ
「溶媒粒子と溶質粒子が別々の行動をとる」
ときにこれらの性質が現れるということです!
これを念頭におきながら,個別の性質を見ていきましょう!
蒸気圧降下
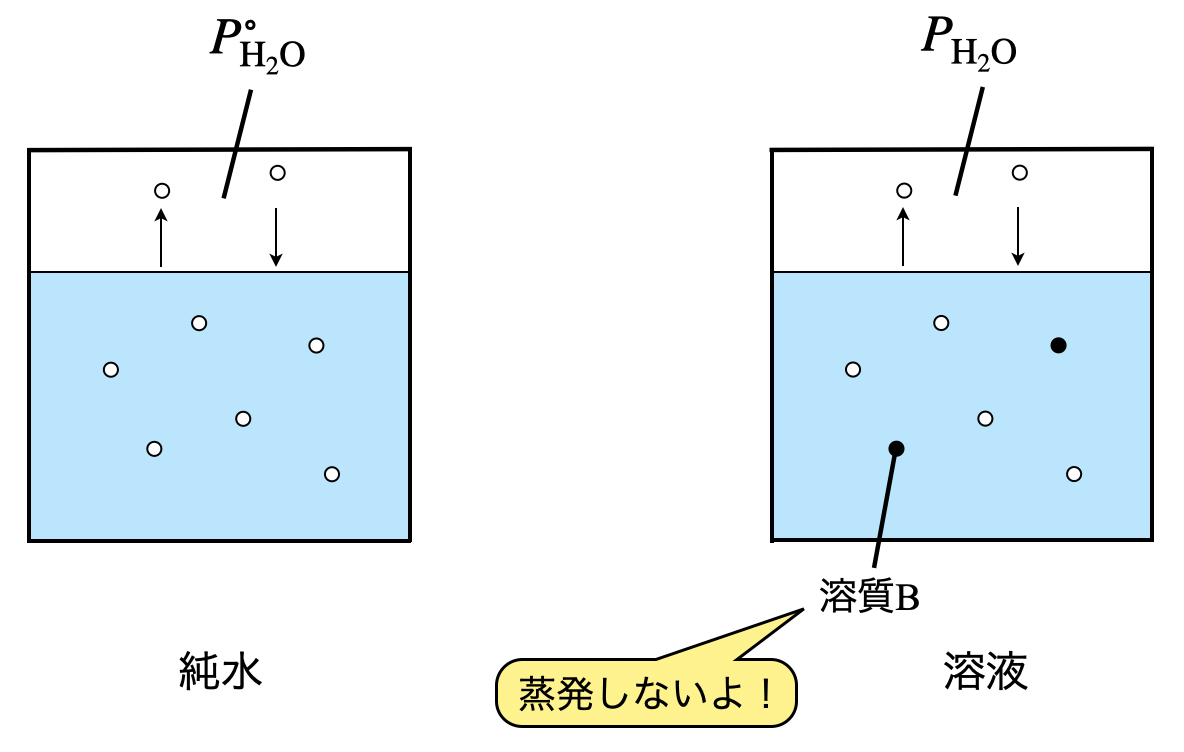
溶媒である水分子\(\rm{H_2O}\)と溶質\(\rm{B}\)を考えてみましょう.ここで,溶質\(\rm{B}\)については液の表面から蒸発しないとします.(この蒸発しないという性質のことを不揮発性といいます!)
溶媒である\(\rm{H_2O}\)は揮発しますが,溶質\(\rm{B}\)は揮発しません.
つまり,「溶媒と溶質で別々の行動をとっています!」
その結果溶液全体で見ると,液の表面から溶媒である\(\rm{H_2O}\)が蒸発しようとすると,溶質\(\rm{B}\)が邪魔するため,溶質\(\rm{B}\)を加えた分だけ蒸気圧が下がることになります.
下図で考えると,\(P_{\rm{H_2O}}^\circ > P_{\rm{H_2O}}\)となります.ここで,\(P_{\rm{H_2O}}^\circ\)は,純水のみの蒸気圧を表しています.このような蒸気圧が下がる現象を蒸気圧降下といいます.
状態図
それでは次に,これらの事象を状態図を使って理解していきましょう.
問題を解くためには,原理を理解することも大切ですが,状態図などの図解ですぐに知識を呼び戻せることが非常に大切です.
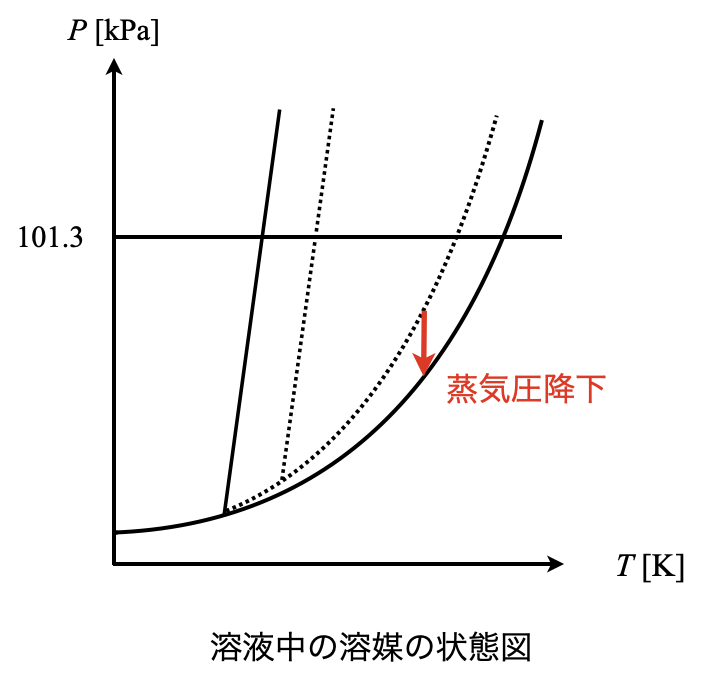
液相から気相へ出ていく溶媒分子が減少しますが,気相から液相へ戻ってくる溶媒分子は変化しません.そのため気液平衡が成り立っていないことになります.この気液平衡を成立させるために,気相から液相へ入る溶媒分子が多くなり,最終的には気相が消えてしまいます.この現象を状態図で考えると,液相の領域が広がり,純溶媒の気液境界線が溶液中の溶媒の液相領域に含まれることとなります.

その中で,蒸気圧降下は気液平衡時の圧力に関する性質です.
ラウールの法則
では,実際にどれくらい蒸気圧が降下するのかを数式を使って見ていきましょう!
蒸気圧降下を以下の\(4\)ステップで考えます.
\(\rm{Step2}\):蒸気圧降下\(\Delta P\)を求める
\(\rm{Step3}\):希薄溶液を考え,近似を使う
\(\rm{Step4}\):質量モル濃度 \(m\ [\rm{mol/kg}]\)で表す
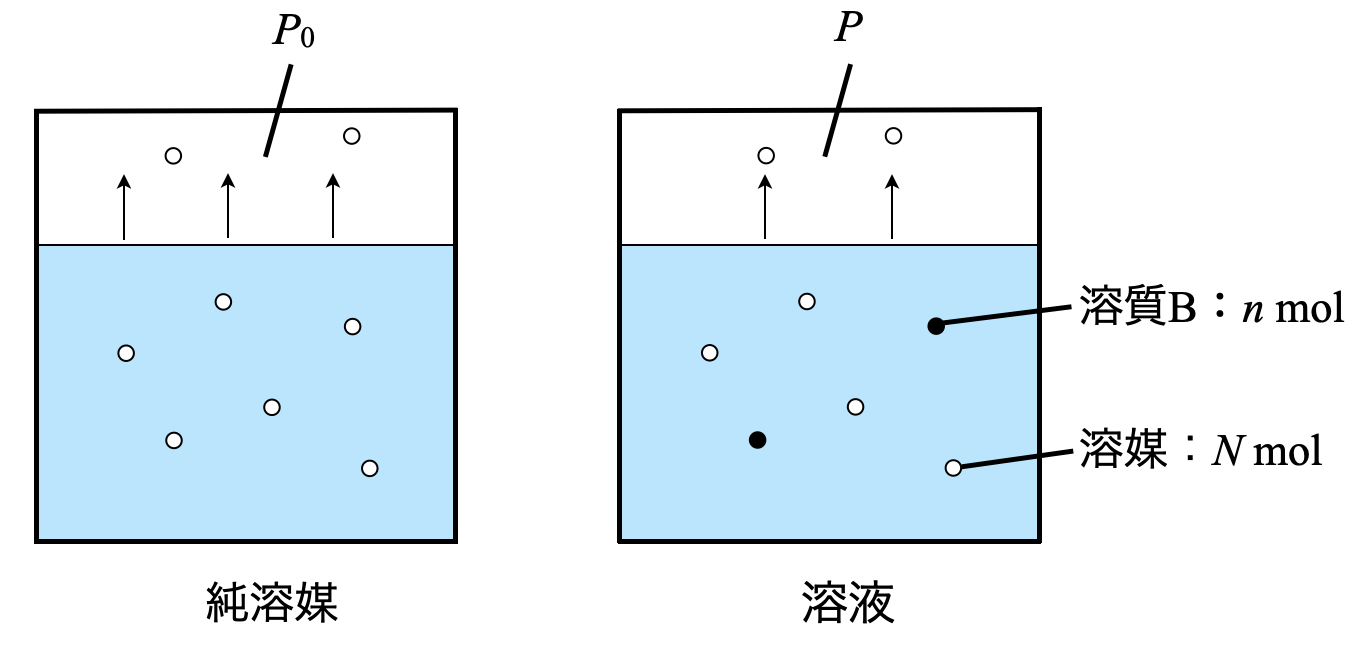
溶液中に溶媒が\(N\ [\rm{mol}]\),溶質が\(n\ [\rm{mol}]\)存在しているとします.
\(\rm{Step1}\)
溶液中の「溶媒」のモル分率は\(\large \frac{N}{N\ +\ n}\)となります.モル分率とは,単位をモルとしたときの割合です!
このときの溶液の蒸気圧\(P\)は以下のように表されます.
\(P = \large \frac{N}{N\ +\ n} \small P_0\)
これは,蒸気圧は溶液中の「溶媒」のモル分率に比例するということです.これをラウールの法則といいます.
例えば,モル分率が\(0.7\)であるとします.
すると,溶液の蒸気圧は\(0.7P_0\)となり,純溶媒の蒸気圧である\(P_0\)よりも降下していることがわかります.モル分率は\(0\)〜\(1\)の間の値をとるため,必ず溶液の蒸気圧は純溶媒の蒸気圧よりも小さくなることがわかります!
このように,わかりにくい公式は実際の数値を使ってイメージを掴めるようにしていきましょう!
\(\rm{Step2}\)
それでは,蒸気圧降下\(\Delta P\)を求めていきます.この\(\Delta P\)は\(P_0\)と\(P\)の差になるため,
\(\Delta P = P_0\ -\ P = P_0\ -\ \large \frac{N}{N\ +\ n} \small P_0 = \large \frac{n}{N\ +\ n} \small P_0\)
ここで注意したいのが,「蒸気圧降下\(\Delta P\)は溶質のモル分率に比例する」ということです!
下にまとめておきますね!
- 溶液の蒸気圧→溶媒のモル分率に比例
- 蒸気圧降下→溶質のモル分率に比例
混乱しないように,しっかりと覚えていきましょう!
\(\rm{Step3}\)
最後に,希薄溶液について考えてみましょう!
希薄溶液とは,溶媒>>溶質となっていて,溶液の濃度が小さい溶液のことです.このような希薄溶液では,\(N>>n\)なので,\(N\ +\ n ≒ N\)とすることができます.
ここも数字を例にして考えてみましょう.
\(N=100000\),\(n=5\)とすると,\(N>>n\)は成り立っていますね!そこで,\(N\ +\ n = 100000\ +\ 5 = 100005\)となって,ほぼ\(100000\)ですよね?
つまり,ほぼ\(N\)として考えることができるというわけです!
すると,
\(\Delta P = \large \frac{n}{N\ +\ n} \small P_0 ≒ \large \frac{n}{N} \small P_0\)
\(\rm{Step4}\)
これに溶媒のモル質量を\(M [\rm{g/mol}]\)として,分母分子にかけていきます!
\(\Delta P = \large \frac{n}{N} \small P_0 = \large \frac{n}{N \cdot M} \small × M P_0 = P_0 M × 10^{-3} \large \frac{n}{N \cdot M × 10^{-3}}\)
\(\large \frac{n}{N \cdot M × 10^{-3}}\)の単位をみると,\(\rm{mol/kg}\)なので,これは質量モル濃度になっています.
これを\(m\)とし,\(P_0M × 10^{-3}\)は定数なので\(k\)とすると,
\(\Delta P= k\ m\)
となります.
近似なども用いて難しくなりましたが,この流れはとても大切なので,しっかりと理解して置いてくださいね!
沸点上昇
蒸気圧降下と同様の条件を考えていきましょう!
先程の容器を加熱し,温度を上げることを考えます.温度を上昇させると,液面のすぐ近くの蒸気の圧力は,その温度で決まる飽和蒸気圧まで増加しており,やがて大気圧と等しくなります.その後,沸騰が起こります.
ここで,沸騰の理解にも注意が必要です.
沸騰とは,「液体の表面だけでなく,液体内部からも蒸気(気泡)が発生する現象」のことをいいます.

この沸騰時の気泡は水分子のみでできていて,そこにでは溶質\(\rm{B}\)は存在しません.すなわち,沸騰という現象時にも溶媒分子と溶質分子は別々に行動します.
この溶液は溶媒と溶質が別々の行動をとるため,蒸気圧降下が生じています.そのためより温度を上げないと蒸気圧を大気圧と等しくできないため,沸点が上昇します.この現象を沸点上昇といいます.
沸点上昇\(\Delta T_{\rm{b}}\)(\(\rm{b:boiling\ point}\))を求めるためには,以下の式を用います.
\(\Delta T_{\rm{b}}\ =\ K_{\rm{b}}\ m\)
ここで,\(K_{\rm{b}}\)はモル沸点上昇と呼ばれる比例定数です.\(m\)は質量モル濃度で,単位は蒸気圧降下のときと同じように\(\rm{mol/kg}\)(溶媒)です.
なぜこの式を用いるのかは大学の熱力学を勉強する必要があるため,沸点上昇については覚えてください!もしリクエストが多ければ,記事にしますね!
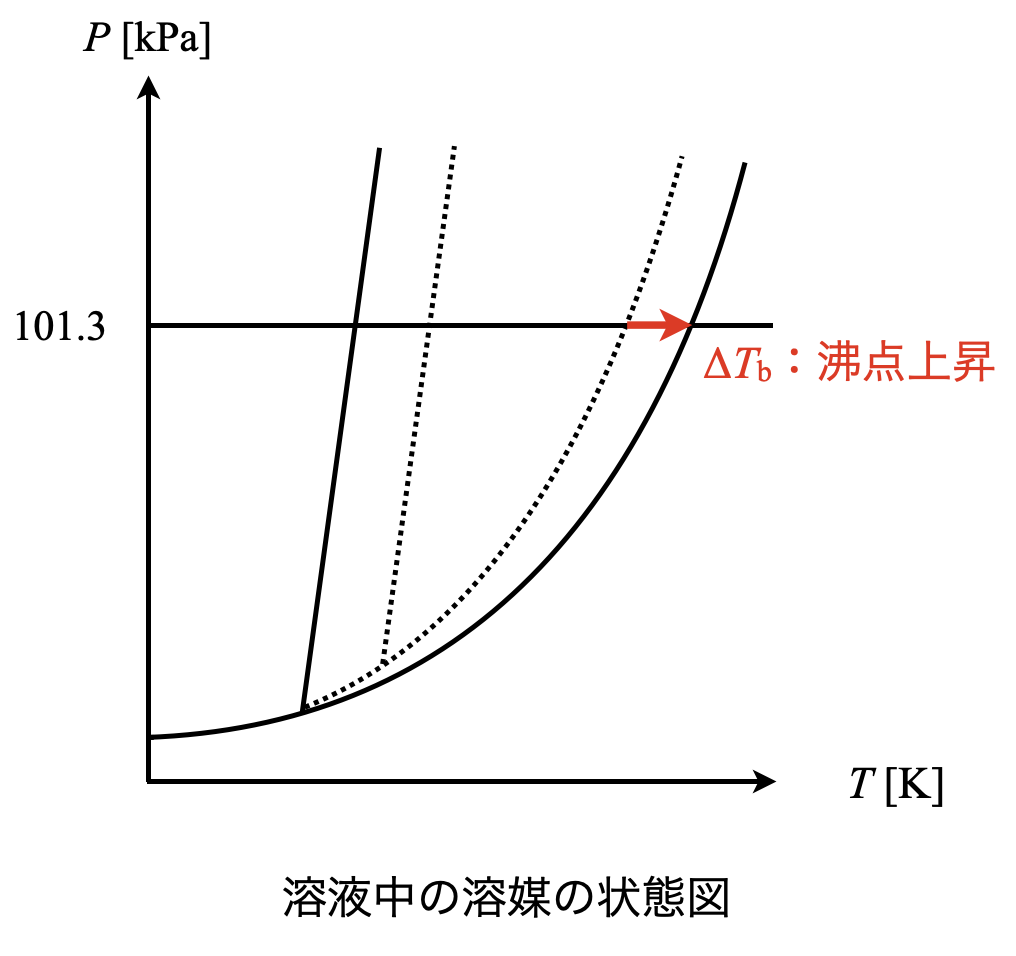
状態図
それでは次に,状態図を使って理解していきましょう.沸点上昇は気液平衡時の温度に関する性質です.
練習問題
では,実際に問題を解きながら,理解を定着させていきましょう!
以下で考える溶液について,ラウールの法則が成り立つとする.
水\(\rm{180\ g}\)にショ糖\(\rm{C_{12}H_{22}O_{11}\ 6.84\ g}\)を溶解した溶液\(\rm{A}\),水\(\rm{180\ g}\)に\(\rm{NaCl\ 5.85\ g}\)を溶解した溶液\(\rm{B}\)を用意した.ただし,\(\rm{25^\circ C}\)における水の飽和蒸気圧は\(\rm{3.13 × 10^3\ Pa}\)であり,\(\rm{H_2O = 18}\),\(\rm{C_{12}H_{22}O_{11} = 342}\),\(\rm{NaCl = 58.5}\)とする.
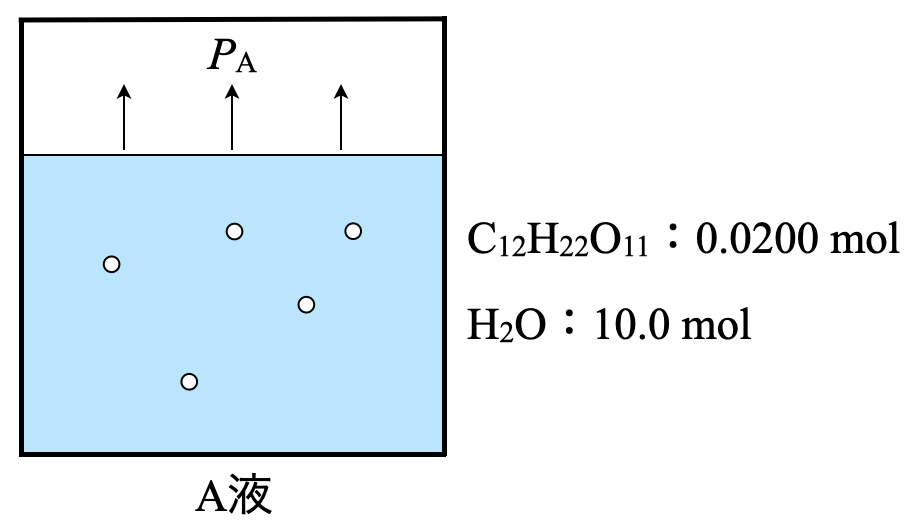
(\(1\))溶液\(\rm{A}\)の蒸気圧\(P_{\rm{A}}\)を求めよ.
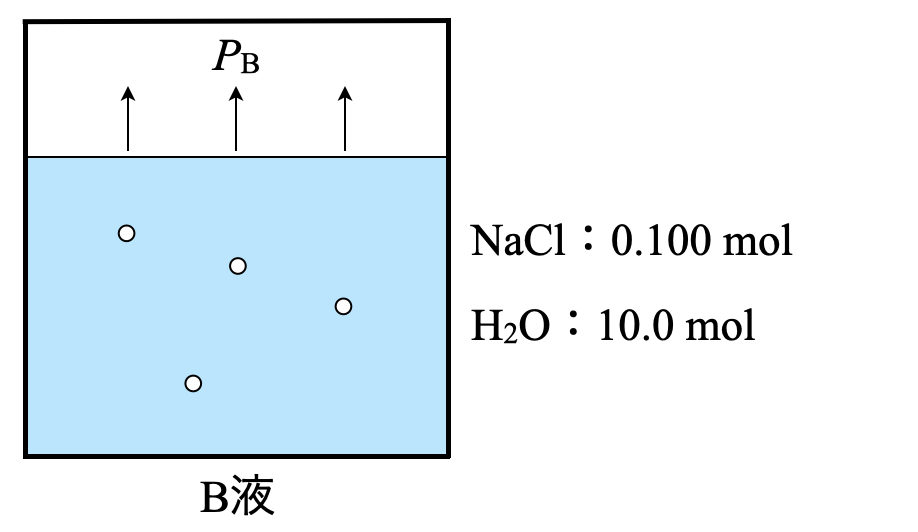
(\(2\))溶液\(\rm{B}\)の蒸気圧\(P_{\rm{B}}\)を求めよ.
(\(3\))この\(2\)つの溶液を図のように連結した.蒸気はどちらの溶液からどちらの溶液へ移動するか?
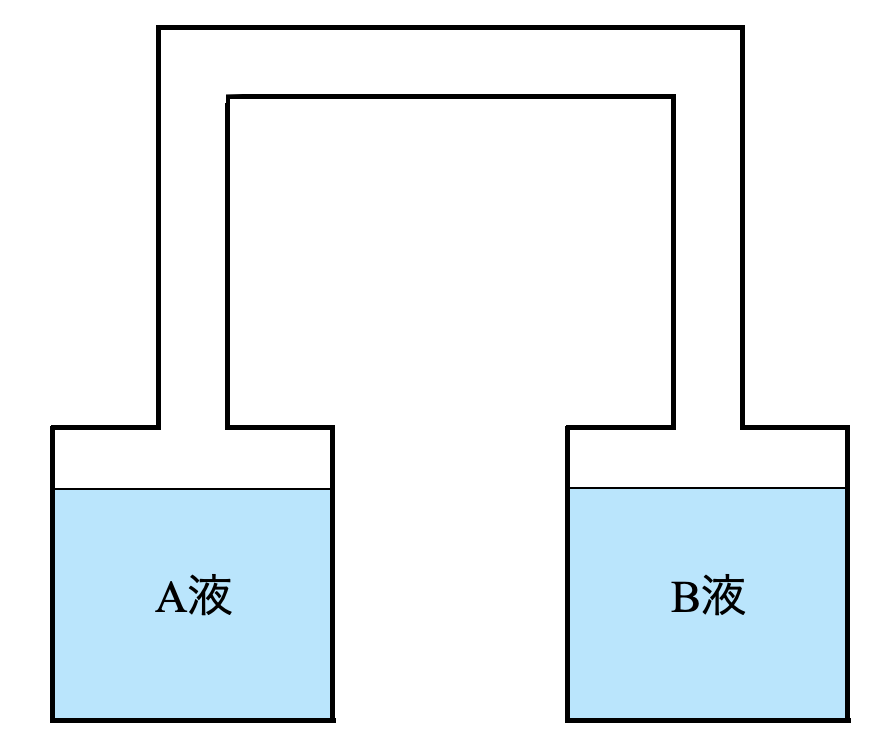
(\(4\))両方の溶液の蒸気圧が等しくなって平行になると水の移動が止まる.このときまで移動した水の物質量はいくらになるか?
この問題は(\(1\))(\(2\))までは基本問題ですが,(\(3\))(\(4\))は少し難易度が高くなっています.ここでしっかりと理解しておくことで,模試などでもライバルと差をつけることができますよ!
それではやっていきましょう!
(\(1\))
蒸気圧を求めるときの\(2\)ステップです!
\(\rm{Step2}\):溶液の蒸気圧はモル分率に比例
\(\rm{Step1}\)
まず,それぞれの物質量を求めましょう!
\(\rm{H_2O:\large \frac{180}{18} \small = 10.0\ mol}\)
\(\rm{C_{12}H_{22}O_{11}:\large \frac{6.84}{342} \small = 0.0200\ mol}\)
よって,溶媒のモル分率は下のようになります.
\(\large \frac{10.0}{10.0\ +\ 0.0200} \small = 0.998\)
\(1\)にとても近いため,この溶液はほぼ水であることがわかります.
\(\rm{Step2}\)
\(P_{\rm{A}} = 3.13\ \rm{kPa × 0.998 = 3.12\ kPa = 3.12 × 10^3\ Pa}\)
(\(2\))
溶液\(\rm{B}\)についても同じように考えていきます.
\(\rm{Step1}\)
\(\rm{H_2O:10.0\ mol}\)
\(\rm{NaCl:\large \frac{5.85}{58.5} \small = 0.100\ mol}\)
よって,溶媒のモル分率は下のようになります.
\(\large \frac{10.0}{10.0\ +\ 0.100} \small = 0.990\)
\(\rm{Step2}\)
\(P_{\rm{B}} = 3.13\ \rm{kPa × 0.990 = 3.10\ kPa = 3.10 × 10^3\ Pa}\)
(\(3\))
(\(1\))(\(2\))より,溶液\(\rm{A}\)の方が水蒸気圧が高いことがわかります.つまり,\(P_{\rm{A}} > P_{\rm{B}}\)となっています.
これをつりあわせるために,水蒸気が\(\rm{A→B}\)へと移動していきます.
そして\(\rm{A→B}\)への水蒸気の移動は,\(\rm{A}\)と\(\rm{B}\)の「質量モル濃度が等しく」なるまで続きます.質量モル濃度が等しくなると,気液平衡の状態となります.
(\(4\))
\(\rm{A→B}\)へ移動した水蒸気量を\(n\ [\rm{mol}]\)とします.
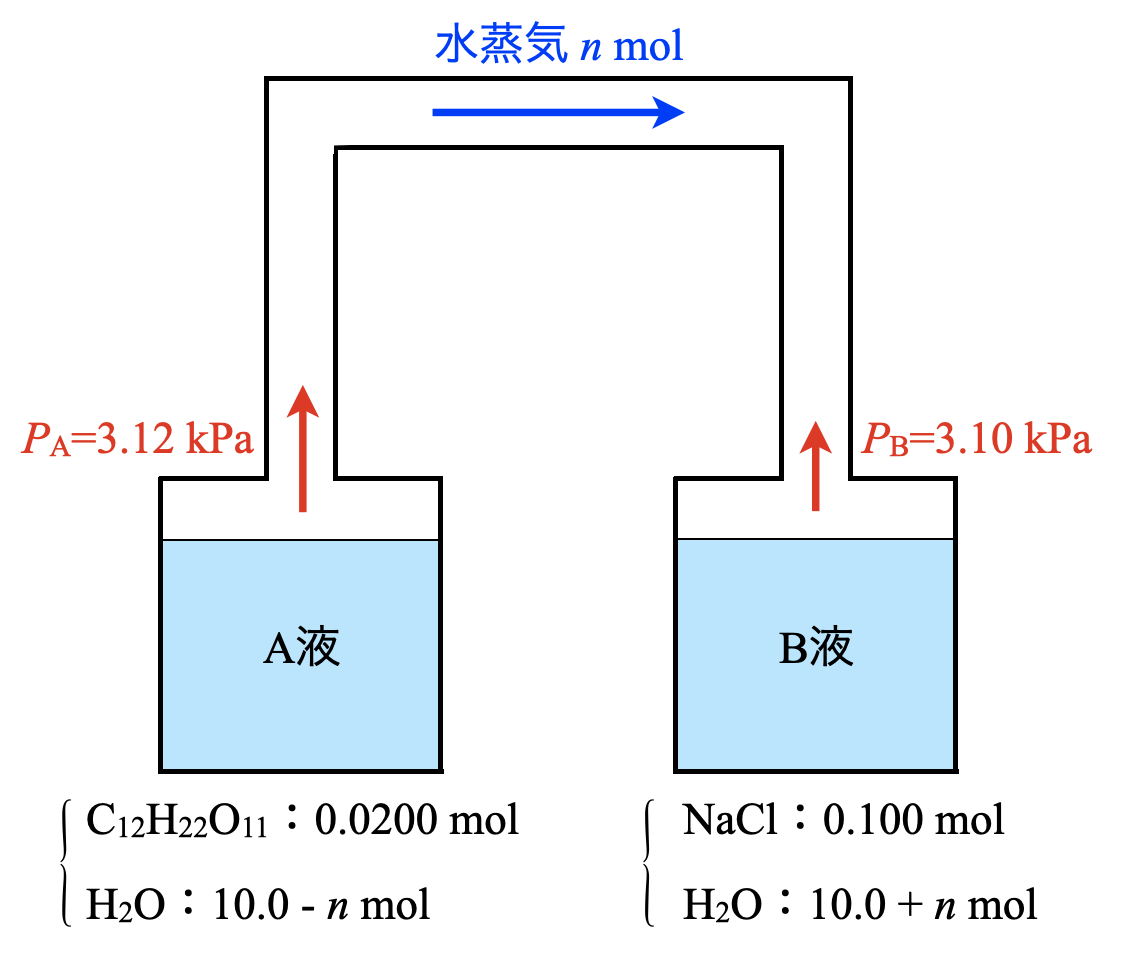
\(\rm{A}\),\(\rm{B}\)のモル分率が等しくなれば,そこから求められる蒸気圧も等しくなります.そのため,ここでの条件である(\(\rm{A}\)の水のモル分率) = (\(\rm{B}\)の水のモル分率)を立式していきます.
\(\rm{A}\)の水のモル分率:\(\large \frac{10.0\ -\ n}{10.02\ -\ n}\)
\(\rm{B}\)の水のモル分率:\(\large \frac{10.0\ +\ n}{10.10\ +\ n}\)
よって,これらから\(n≒6.67\ \rm{mol}\)とわかります.
今回の問題のポイントは,まず溶液の蒸気圧を求められるようになることでした.そして,蒸気圧の異なる溶液を連結したときには,両方の蒸気圧が等しくなるように,上記が移動します.その条件は,「水のモル分率」を等しくするということです.
今日はここまでです!お疲れ様です!
しっかり復習してくださいね!



コメント