
それでは今日も元気よく勉強していきましょう!
\(\rm{O}\)系列の全体像
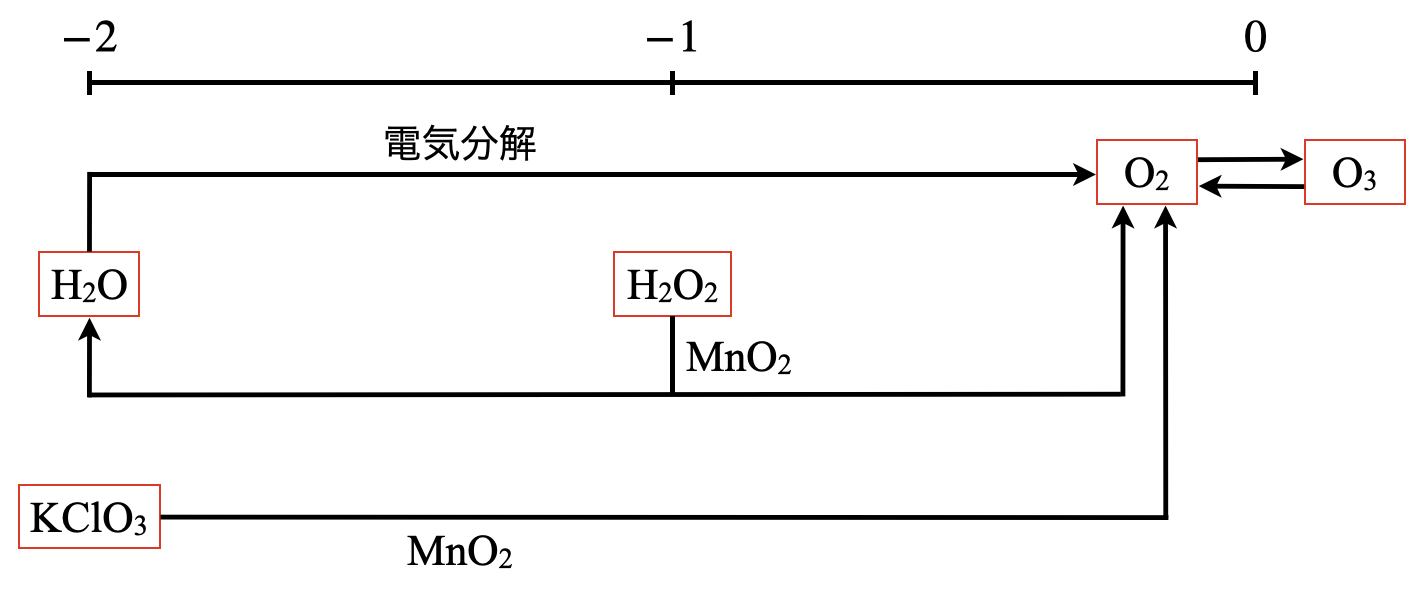
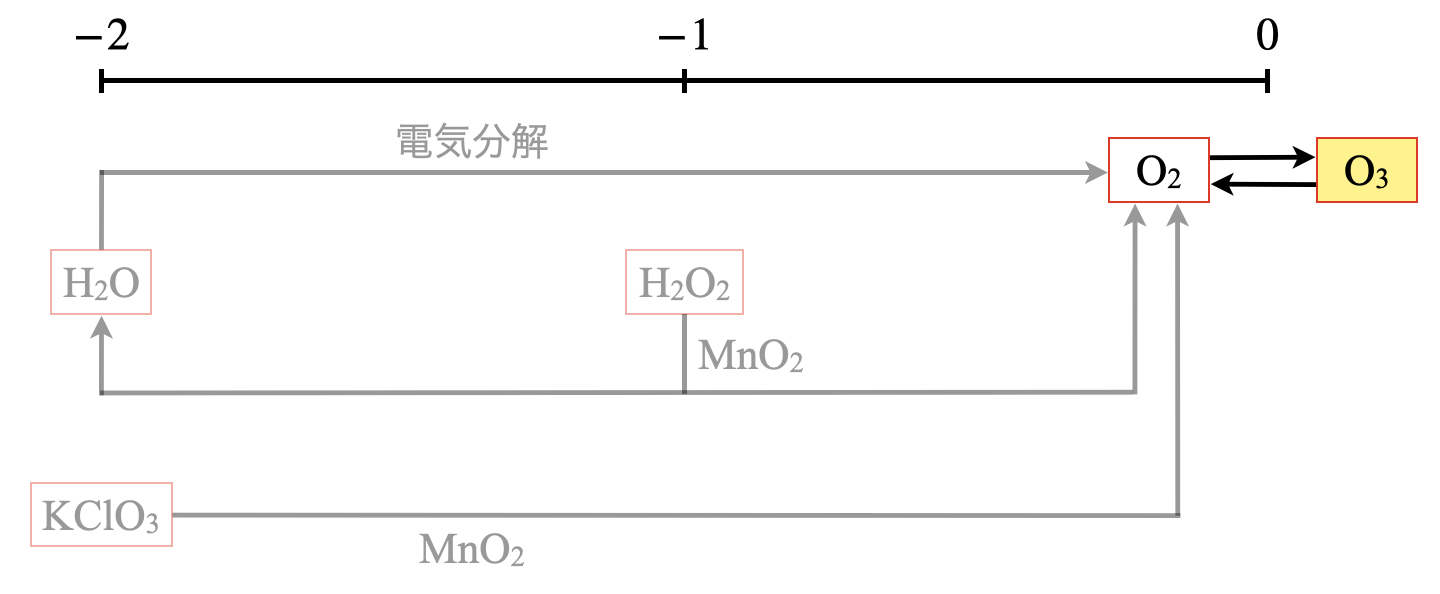
\(\rm{O}\)原子のとりえる酸化数は\(-2\)〜\(0\)になります.
\(\rm{N}\)系列や\(\rm{S}\)系列と比較すると,\(\rm{O}\)系列の全体像がだいぶ簡単に見えてきますね!
\(\rm{O}\)系列の気体は\(\rm{O_2}\)と\(\rm{O_3}\)なので,下の各項でそれぞれ深堀りしていきましょう!
酸素
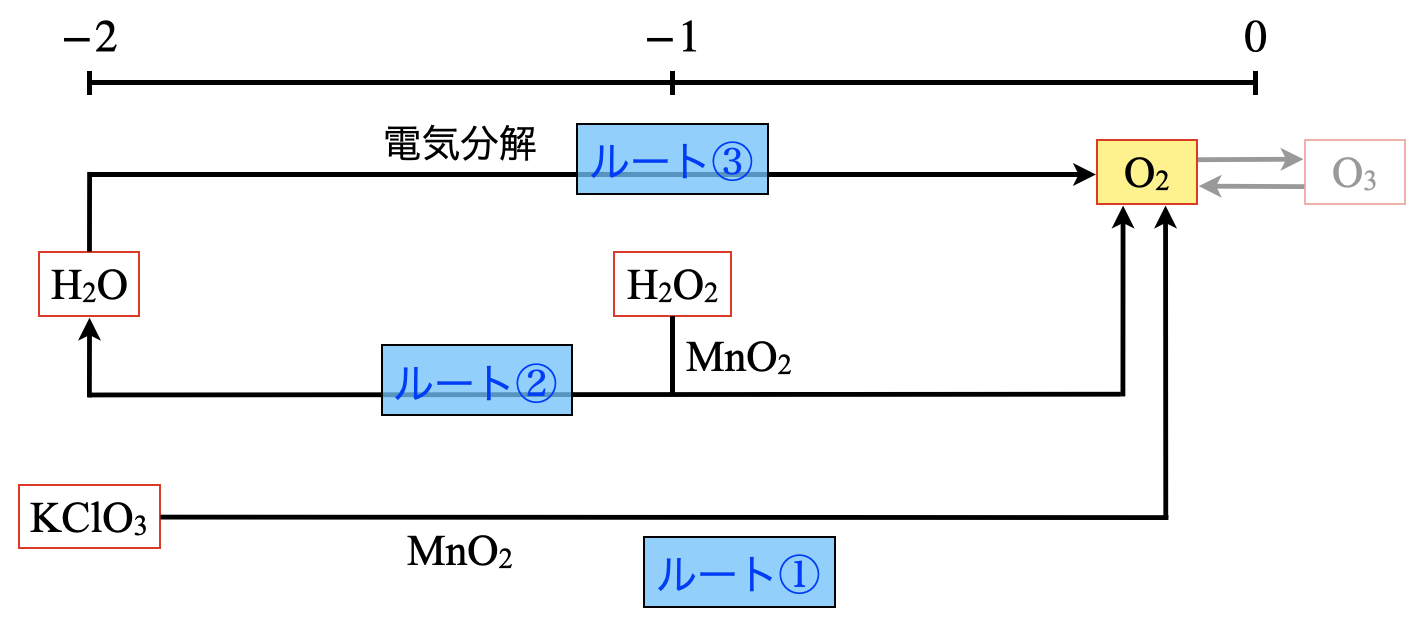
\(\rm{O_2}\)は次の\(3\)ルートから生成していきます.
ルート\(\rm{2:H_2O_2→O_2}\)
ルート\(\rm{3:H_2O→O_2}\)
それぞれ詳しくみていきましょう!
\(\rm{KClO_3}\)ルート
それではまず\(\rm{KClO_3}\)ルートをみていきましょう!
\(\rm{KClO_3}\)(塩素酸カリウム)の\(\rm{Cl}\)の酸化数を考えると,\(+5\)となります.一方で\(\rm{Cl}\)の安定的な酸化数は\(-1\)であるため,\(\rm{KClO_3}\)は酸化数的に考えると不安定であることがわかります.そのため,\(\rm{KClO_3}\)は分解しようとしますが,そのままでは分解しません.
そこで,お助けマンが登場します!
それが「\(\rm{MnO_2}\)」です!
さらにこの触媒に熱を加えます!
すると,\(\rm{Cl}\)は安定な酸化数である\(-1\)になり,この相手は陽イオンである\(\rm{K^+}\)がします.最後に,\(\rm{O}\)原子がはじきだされ,\(\rm{O_2}\)になるしかない!というわけです.
この一連の出来事を反応式に表すと以下のようになります.
\(\rm{2KClO_3\ →\ 2KCl\ +\ 3O_2}\)
「\(\rm{KClO_3}\)から\(\rm{O}\)原子がはじきだされて,\(\rm{O_2}\)が生成する!」という流れを覚えることで,この反応式のイメージがしやすくなると思います!
\(\rm{H_2O_2}\)ルート
次に,\(\rm{H_2O_2}\)ルートをみていきましょう!
\(\rm{O}\)の安定な酸化数は\(-2\)ですが,\(\rm{H_2O_2}\)(過酸化水素)の\(\rm{O}\)の酸化数は\(-1\)です.こちらも先ほどと同じように,触媒として\(\rm{MnO_2}\)を用いることで,\(\rm{O}\)原子がはじきだされ,\(\rm{O_2}\)が生成します.
\(\rm{2H_2O_2\ →\ 2H_2O\ +\ O_2↑}\)
この場合は,\(\rm{MnO_2}\)を加えることで加熱しなくても容易に分解します.これが先ほどの\(\rm{KClO_3}\)ルートと異なる点になります.
\(\rm{H_2O}\)ルート
最後のルートとして,\(\rm{H_2O}\)ルートを解説します!
\(\rm{H_2O}\)から\(\rm{O_2}\)を生成するのは非常に難しいので,電気分解を使用します.水の電気分解として\(2\)パターン覚えてほしいので順に解説していきますね!
\(\rm{H_2SO_4}\)水溶液の電気分解
まずは基本となる酸性水溶液の電気分解から考えていきましょう!
電気分解の考え方は\(3\)ステップです!
\(\rm{Step2:}\)陰極での\(e^-\)の受け取り反応の決定!
\(\rm{Step3:}\)陽極での\(e^-\)の放出反応の決定!
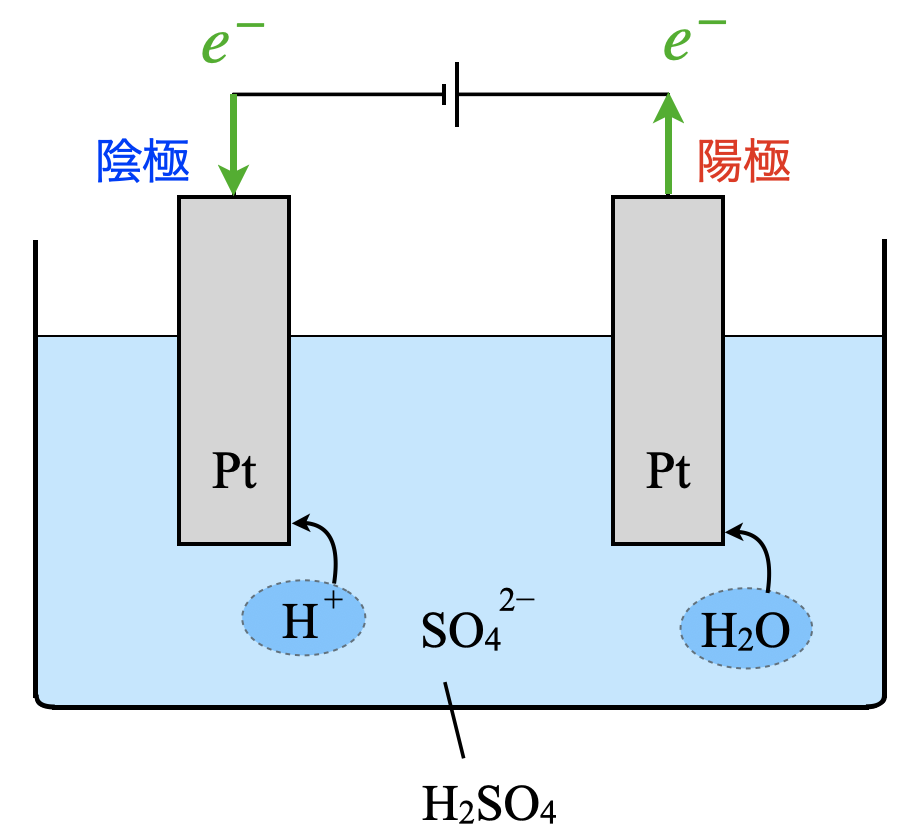
\(\rm{Step1}\)
\(e^-\)は電流の流れる方向と逆になります.そのため電池の負極とつながっている方が陰極,正極とつながっている方が正極となります.
\(\rm{Step2}\)
水溶液中には,\(\rm{Pt}\),\(\rm{H^+}\),\(\rm{SO_4^{2-}}\),\(\rm{H_2O}\)の物質があります.この中で\(e^-\)を受け取れる物質は,\(\rm{H^+}\)のみとなります.
\(\rm{2H^+\ +\ }\)\(2e^-\ \rm{→\ H_2}\)
\(\rm{Step3}\)
水溶液の中で\(e^-\)を放出できるのは,\(\rm{Pt}\)と\(\rm{H_2O}\)中の\(\rm{O^{2-}}\)になります.ここで,\(\rm{Pt}\)は非常に安定しているので,\(e^-\)を放出することはありません.イオン化傾向を考えても非常に小さいので,イオンではなく単体でいたいことがわかりますね!
\(\rm{2H_2O\ →\ O_2\ +\ 4H^+\ +\ }\)\(4e^-\)
ここで,\(\rm{Step2}\)と\(3\)の各反応式の\(e^-\)の数を合わせて足すと,下のようになります.
\(\rm{2H_2O\ →\ 2H_2\ +\ O_2}\)
これは中学校のときに勉強した水の電気分解の式ですね!
\(\rm{NaOH}\)水溶液の電気分解
次に,塩基性水溶液の電気分解を考えてましょう!
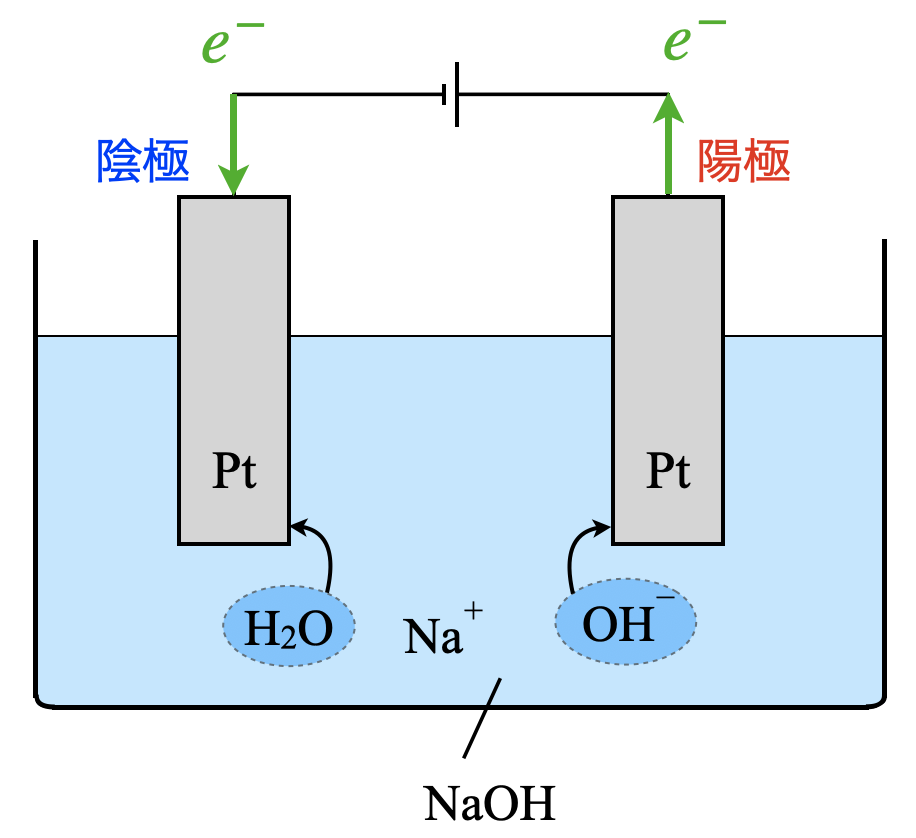
考え方のステップは酸性水溶液の電気分解のときとまったく同じですよ!
\(\rm{Step1}\)
先ほどと同じように電池の負極側が陰極,正極側が正極となります.
\(\rm{Step2}\)
水溶液中には,\(\rm{Pt}\),\(\rm{Na^+}\),\(\rm{H_2O}\),\(\rm{OH^-}\)の物質があります.この中で\(e^-\)を受け取れる物質は,\(\rm{Na^+}\)と\(\rm{H_2O}\)になります.ここで,\(\rm{Na^+}\)はイオン化傾向が大きく,\(\rm{Na^+ >> H^+}\)なので,\(\rm{H^+}\)が\(e^-\)を受け取ります.
ただ,ここで先ほどと違う点はこの水溶液が塩基性である!という点です.
この\(\rm{H^+}\)は\(\rm{H_2O}\)から生じたごくわずかのものです.そこで,先ほどの\(\rm{2H^+\ +\ }\)\(2e^-\ \rm{→\ H_2}\)の\(\rm{H^+}\)を\(\rm{H_2O}\)から生じたように書き直します.
\(\rm{2H_2O\ +\ }\)\(2e^-\ \rm{→\ H_2\ +\ 2OH^-}\)
\(\rm{Step3}\)
水溶液の中で\(e^-\)を放出できるのは,\(\rm{Pt}\),\(\rm{OH^-}\)になります.ここでも非常に安定している\(\rm{Pt}\)は,\(e^-\)を放出することはありません.そのため,\(e^-\)を放出できるのは,\(\rm{OH^-}\)のみとなります.
\(\rm{4OH^-\ →\ O_2\ +\ }\)\(4e^-\ \rm{+\ 2H_2O}\)
ここでも,\(\rm{Step2}\)と\(3\)の各反応式の\(e^-\)の数を合わせて足すと,下のようになります.
\(\rm{2H_2O\ →\ 2H_2\ +\ O_2}\)
これも水の電気分解の式ですね!
ここでの注意点は,水溶液中に存在する\(\rm{NaOH}\)は結局分解されていないということです!
\(\rm{Na}\)のイオン化傾向が大きすぎるために,分解できないのですね!
この\(\rm{NaOH}\)を分解する方法については,今後記事を書いていきますね!
オゾン
オゾンは酸素の同素体です.
オゾンは酸素中で無声放電をするか,酸素に強い紫外線を当てることで生成します.
\(\rm{3O_2\ ⇄\ 2O_3}\)
オゾンは淡青色の有毒気体です.オゾンについて覚えておいていただきたい性質を\(3\)つ紹介します!
①酸化作用
②ヨウ素デンプン反応
③共鳴
①酸化作用
オゾンは分解して酸素に変わりやすく,このとき強い酸化作用を示します.そこで,空気の殺菌や消臭,繊維の漂白および水道水の最終処理などに使われています.
②ヨウ素デンプン反応
オゾンは湿らせたヨウ化カリウムデンプン紙を青色に変化させることで検出します.この反応は以下のようになります.
\(\rm{2KI\ +\ O_3\ +\ H_2O\ →\ I_2\ +\ 2KOH\ +\ O_2}\)
この反応は\(\rm{O_3}\)などの酸化剤によって\(\rm{KI}\)が酸化されて\(\rm{I_2}\)が生じています.
③共鳴
オゾンの構造式は次のようになっています.
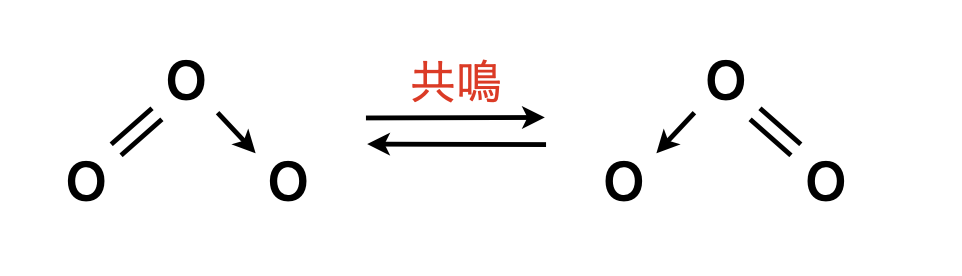
両者が交互に入れ替わっており,実際の分子の姿はこの\(2\)つを重ね合わせた状態になっています.このような状態を共鳴しているといいます.
共鳴することで,電子が自由に動けるようになり,エネルギー的に安定します.このエネルギーのことを共鳴エネルギーといいます.
練習問題
それでは今日解説したものに関連した計算問題を解いていきましょう!
(\(1\))\(\rm{10\ L}\)の酸素気体に無声放電すると体積が同温,同圧下で\(\rm{9.8\ L}\)となった.\(\rm{O_2}\)の何\(\%\)が\(\rm{O_3}\)に変化したか?
(\(2\))\(\rm{KI(aq)}\)に\(\rm{1000\ L}\)(\(\rm{27^\circ C}\),\(\rm{1.0 × 10^5\ Pa}\))の空気を通したところ空気中の\(\rm{O_3}\)が\(\rm{KI}\)と反応して吸収された.生じた\(\rm{I_2}\)を\(\rm{0.10\ mol/L}\)の\(\rm{Na_2S_2O_3}\)で滴定すると\(\rm{2.0\ mL}\)必要であった.空気中の\(\rm{O_3}\)の体積は何\(\%\)であるか?
気体定数 \(R = 8.3 × 10^3\ \rm{Pa \cdot L/mol \cdot K}\)
(\(1\))
状態方程式:\(pV = nRT\)で,\(p\),\(T\)一定なので,
\(V = \large \frac{nRT}{p} \small = \large \frac{RT}{p} \small \cdot n = k × n\)
となります.つまり,\(n\)(モル)\(→V\)(体積)で考えて\(\rm{OK}\)というわけですね!
次に,酸素を無声放電すると下のような反応が起こるのでしたね!
\(\rm{3O_2\ ⇄\ 2O_3}\)
\(\rm{O_2}\)が初め\(\rm{10\ L}\)あり,\(10\alpha\ \rm{L}\)変化したとします.
ここでのポイントは変化量を\(x\ \rm{L}\)ではなく,\(10\alpha\ \rm{L}\)としている点です.
これにより,最終量が\(10(1 – \alpha)\ \rm{L}\)となり,この\(\alpha\)が空気中の\(\rm{O_3}\)の体積比率を表しているということです!このようにすることで,計算も楽になりますよ!
\(\rm{O_3}\)については,変化量が\(10 \alpha × \large \frac{2}{3} \small = \large \frac{20}{3} \small \alpha\)となります.最終量の合計が\(\rm{9.8\ L}\)となるので,ここで等式を作ることができます!
ここまでをまとめると下のようになります.

\(10(1-\alpha) + \large \frac{20}{3} \small \alpha = 9.8\)
これを解くと,
\(\alpha = 0.06 = 6\%\)
(\(2\))
この問題は\(3\)ステップで考えていきます!
\(\rm{Step2:I_2}\)の\(\rm{Na_2S_2O_3}\)による滴定
\(\rm{Step3:}\)モル比を考えて計算実行!
まずこの問題の流れを図示すると,下のようになります.
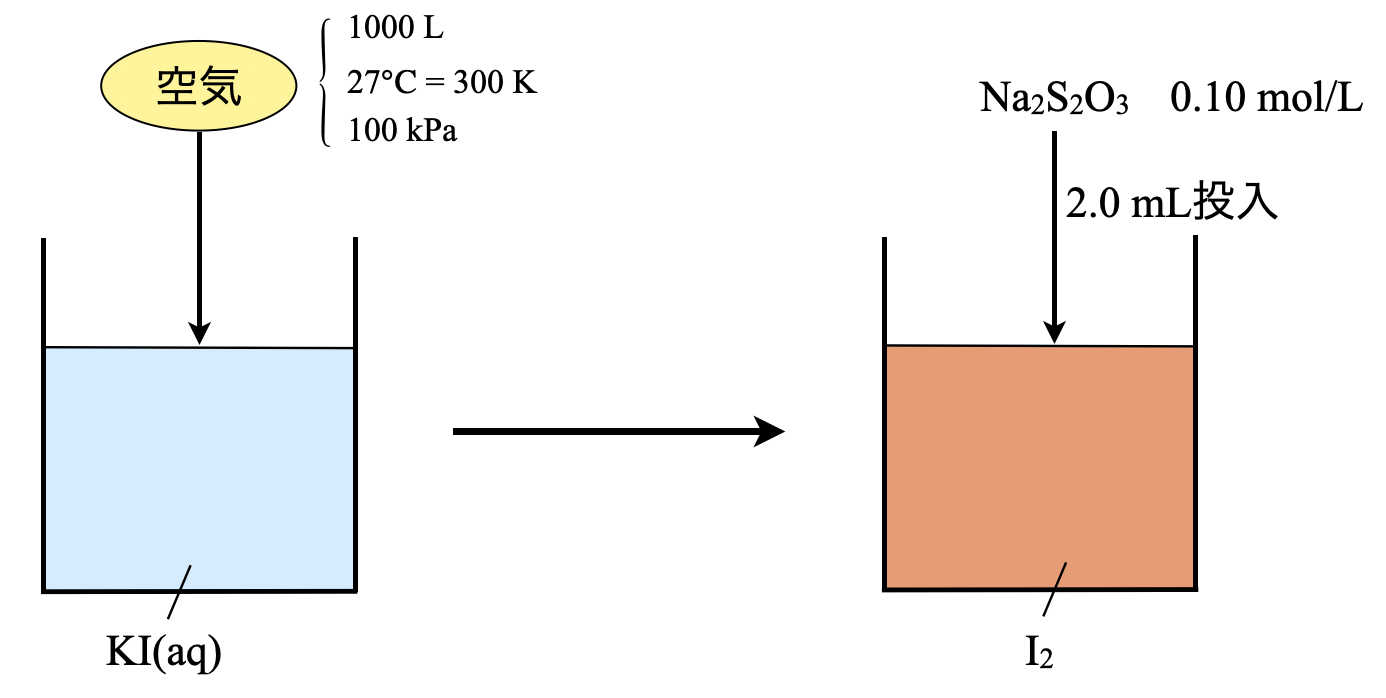
\(\rm{Step1}\)
まず反応式を考えていきましょう!
\(\rm{O_3\ +\ 2KI\ +\ H_2O\ →\ I_2\ +\ 2KOH\ +\ O_2}\)
ここでのポイントは\(\rm{O_3:I_2 = 1:1}\)になっているということです!ここで発生した\(\rm{I_2}\)を\(\rm{Step2}\)で滴定します.
\(\rm{Step2}\)
\(\rm{I_2}\)の\(\rm{Na_2S_2O_3}\)による滴定反応は以下のようになります.
\(\rm{I_2\ +\ 2Na_2S_2O_3\ →\ 2NaI\ +\ Na_2S_4O_6}\)
ここで\(\rm{I_2}\)と\(\rm{Na_2S_2O_3}\)のモル比を考えると,\(\rm{I_2:Na_2S_2O_3 = 1:2}\)となります.
\(\rm{Step3}\)
\(\rm{Step1}\)と\(2\)をまとめると,\(\rm{O_3:I_2:Na_2S_2O_3 = 1:1:2}\)となります.
まず,\(\rm{Na_2S_2O_3}\)を使ったモルを計算しましょう.
\(\rm{0.10 × 2.0 = 0.20\ mmol}\)
\(\rm{O_3:Na_2S_2O_3 = 1:2}\)なので,\(\rm{O_3 = 0.10\ mmol}\)となります.
ここで\(\rm{O_3}\)の体積を状態方程式\(:pV = nRT\)を使って求めていきましょう!気体定数\(R\)は\(R = 8.3\ \rm{kPa \cdot L/mol \cdot K}\)と単位変換して使用します!
\(V_{\rm{O_3}} = \large \frac{nRT}{p} \small = \large \frac{0.10\ ×\ 8.3\ ×\ 300}{100} \small = 2.49\ \rm{mL} = 2.49 × 10^{-3}\ \rm{L}\)
これは空気\(\rm{1000\ L}\)あたりの値であるため,
\(\large \frac{2.49 × 10^{-3}}{1000} \small × 100 = 2.49 × 10^{-4} = 2.5 × 10^{-4}\%\)
この問題はモル比をしっかりと捉えることで余分な計算を省き,正確に早く解くことができます!このように問題の全体像を捉えられるように一緒に頑張っていきましょう!
今日は以上となります!お疲れ様です!!
今日も覚えることが多くて大変ですが,覚えるときにはなぜそうなるのか?を必ずおさえながら覚えるようにしてくださいね!
今後もあなたの「なぜ」を大切にしながら詳しく解説していきます!



コメント