【明快】理想気体と実在気体の性質の違いは？わかりやすく解説！！

KUT

今回は理想気体と実在気体の違いについて学習していきます．
実在気体については，覚えるべきポイントが絞られているので，そこを重点に覚えていきましょう！
今日も頑張りましょう！

実在気体と理想気体

まず，理想気体について簡単に復習しておきましょう！
理想気体は状態方程式である\(\ pV\ =\ nRT\)を用いることができます．
この場合，粒子体積が\(\ 0\)で分子間力が働いていないとして考えています．

しかしながら，実際の気体は粒子体積もあり，分子間力も存在しています．
このような気体のことを実在気体と言います．
そのため，状態方程式である\(\ pV\ =\ nRT\)を用いることはできません．
記事の中で実在気体に関する方程式を紹介しますね！

そこでまず，実在気体について考え，理想気体に近づける方法を見ていきましょう！
 
 

実在気体を理想気体に近似できる条件

理想気体とは分子間力\(f\)，粒子体積\(v\)がともに\(\ 0\)である気体のことをいいます．

実在気体では，分子間力\(\ f=0\)，粒子体積\(\ v=0\)とすることはできませんが，\(f→0，v→0\)とすることはできます．その手段として，\(2\)つ考えてみましょう！
 
 

①高温にする
一般に，分子の運動エネルギーは\(\large \frac{1}{2} \small mv^2\)と表されます．そのため高温にすると，分子のもつ運動エネルギーは顕著に増加します．
粒子がより高速で動くため．相対的に分子間に働く分子間力を無視できるようになるわけです．
 
 

②低圧にする
\(n，T\)を一定にして低圧にすると，容器内の体積が増加します．気体全体の体積に対して分子自身の粒子体積は無視できるほど小さくなり，分子間距離は大きくなります．そのため，分子の間に働く分子間力の影響も小さく無視できるというわけです．

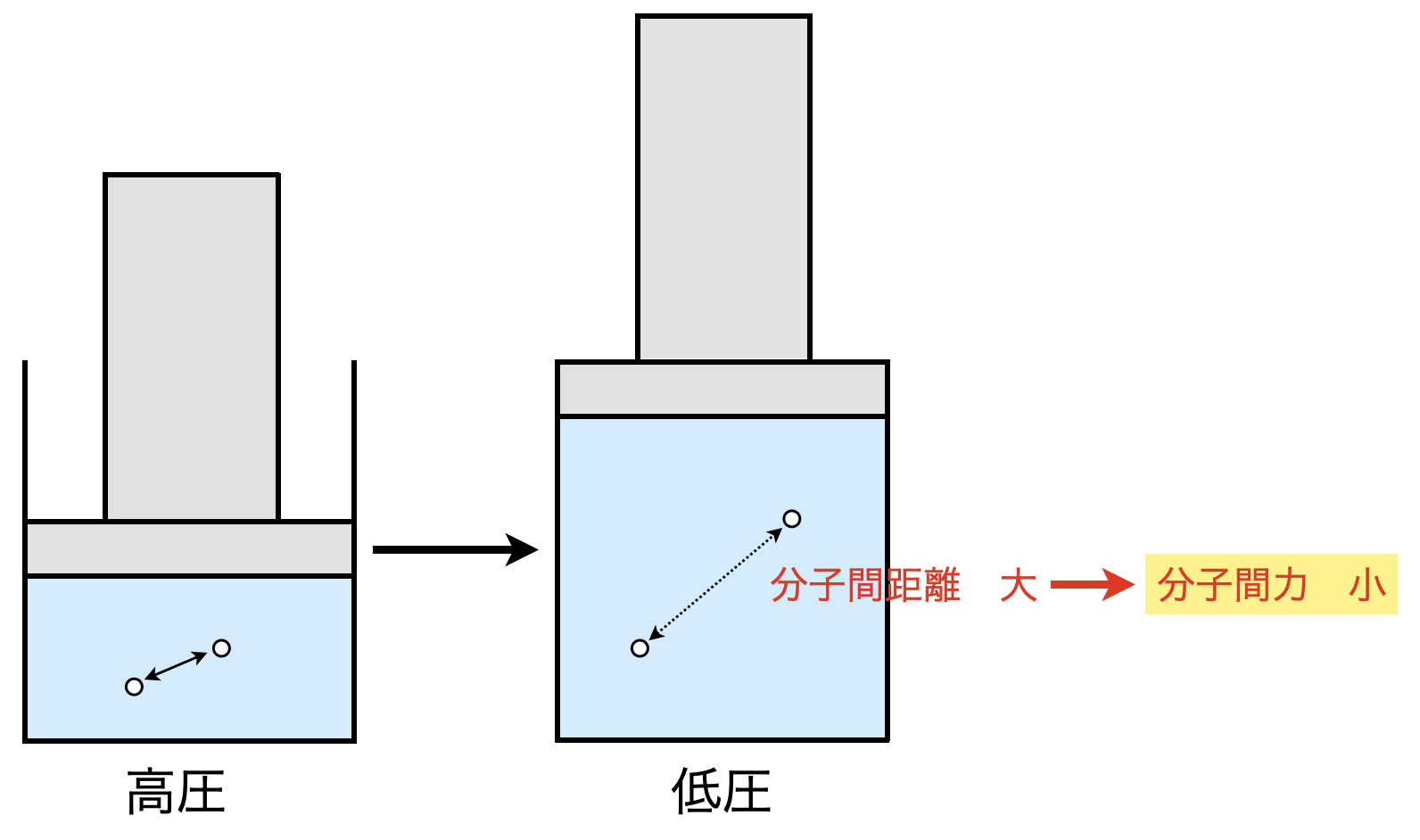
以上より，実在気体を理想気体に近づける条件は，高温・低圧にすることです！

実在気体の状態方程式

実在気体の状態方程式には，様々なものがありますが，有名なものにファンデルワールス（\(\rm{van\ der\ Waals}\)）の状態方程式があります．これについて詳しく考えていきましょう！
 
 
まず理想気体の状態方程式である
\(p_i V_i\ =\ nRT\)
が成り立ちます．
ここで添字の\(i\)は理想（\(\rm{ideal}\)）を表しています．

上の式の中で，\(p_i・V_i\)と\(p_r・V_r\)の違いを評価していきます．
ここの添字である\(r\)は実在（\(\rm{real}\)）を表しています．

実在体積Vr

実在気体では，自分の粒子の体積によって自由に運動できる空間が減少しています．そのため，自分の粒子の体積分を減少させる必要があります．容器内に粒子が\(n\)個あるとすると，減少させる体積は\(n\)に比例するので，\(b\ ×\ n\)となります．
よって，\(V_i\ =\ V_r\ -\ nb\ \)となります．

実在圧力pr

実在気体では，粒子間に引力が働き，それにより壁に衝突する力が減少します．粒子間が近づく頻度と分子間力が関係していると考えられます．これは\(\large \frac{n}{V} \small × \large \frac{n}{V}\)に比例すると考えて良いです．
そのため，
\(p_i\ =\ p_r\ +\ a \left(\large \frac{n}{V} \right)^2 \)
となります．
 
 
これを理想気体の状態方程式：\(p_i V_i\ =\ nRT\)に代入すると，
\(\left(p_r\ +\ a \left(\large \frac{n}{V} \right)^2 \right)(V_r\ -\ nb)\ =\ nRT\)
となります．
 
 
これをファンデルワールス（\(\rm{van\ der\ Waals}\)）の状態方程式といい，実在気体のかなり広い圧力範囲で成り立ちます．

実在気体と理想気体のズレ

実在気体が理想気体からどれほどズレているのかを知るために，圧縮因子\(Z\)というものがります．
\(1\ \rm{mol}\)の理想気体について，状態方程式から導かれる\(Z\)の値は圧力・温度に関係なく必ず\(1\)となります．
下の式を見ると，簡単に理解できますね！
\(pV\ =\ RT\)より，\(Z\ =\ \large \frac{pV}{RT}\ \small =\ 1\)
 
 
 

しかしながら，実在気体では，圧縮因子\(Z\)は\(1\)にはなりません．
これを考えるためには，\(n，p，T\)一定で比較します．

圧縮因子について，
実在気体：\(Z\ =\ \large \frac{pV_r}{RT}\)

理想気体：\(1\ =\ \large \frac{pV_i}{RT}\)
そのため，

\(Z\ =\ \large \frac{V_r}{V_i}\)

となります．つまり，\(Z\)は実在気体の体積が理想気体の体積の何倍かを示す値であることが分かります．

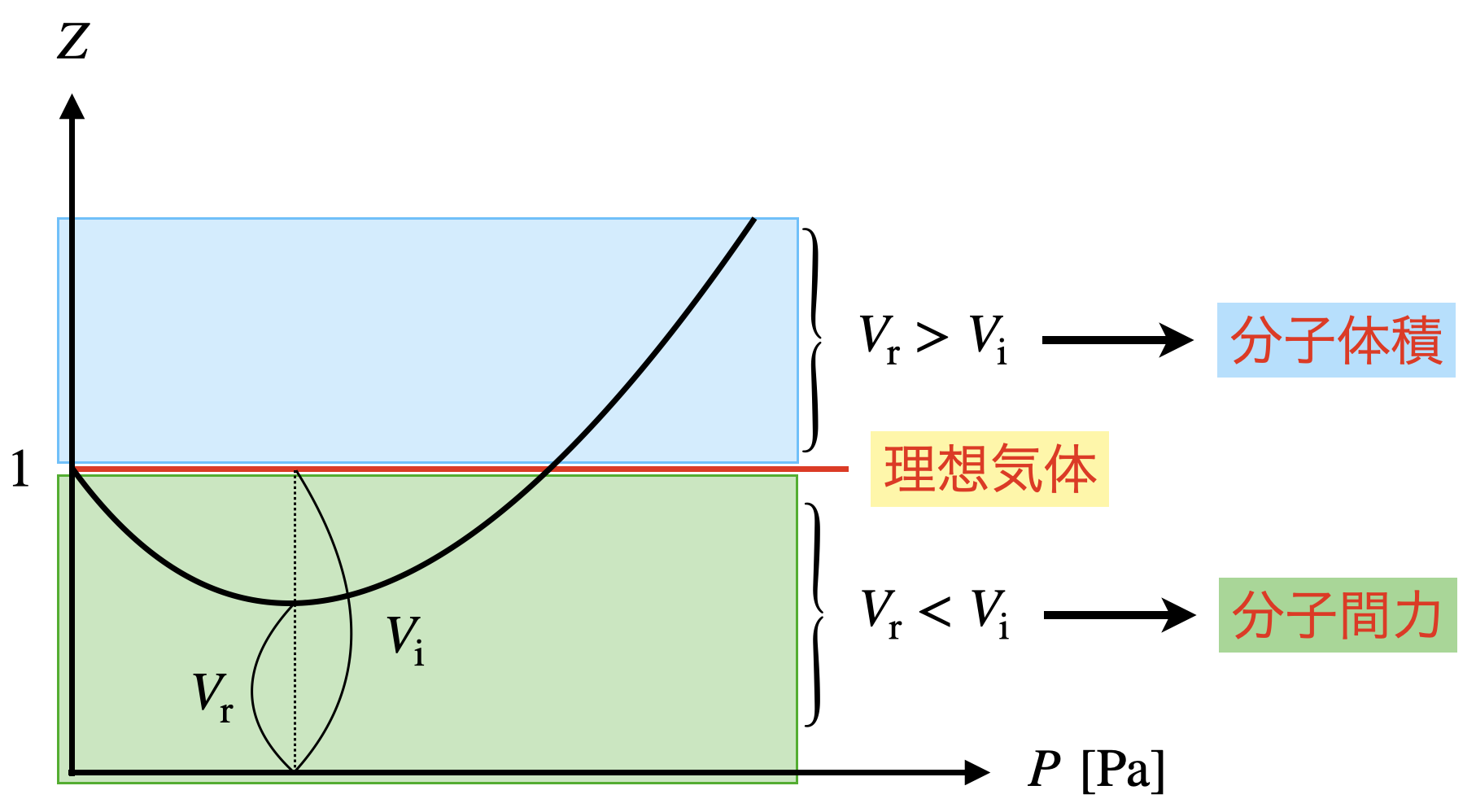
①\(\ Z\ <\ 1\)のとき
\(V_r\ <\ V_i\) となります． これは分子間力の効果になります．圧力を加えると，分子が近づくことで，粒子間引力が働き，理想気体より体積減少します．

②\(\ Z\ >\ 1\)のとき
\(V_r\ >\ V_i\)となります．
これは分子体積の効果によります．さらに圧力を加えると，気体の体積と比較して分子自身の体積を無視することができなくなります．